16. Виды относительных величин

Рассмотрим следующие виды относительных величин.

1. Относительная величина выполнения договорных обязательств – это показатель, характеризующий уровень выполнения предприятием своих обязательств, предусмотренных в договорах. Расчет показателя производится путем соотношения объема фактически выполненных обязательств и объема обязательств, предусмотренных в договоре. Выражается он в форме коэффициентов или в процентах.

2. Относительные величины структуры – это показатели, характеризующие долю от состава изучаемых совокупностей. Относительная величина структуры определяется отношением абсолютной величины отдельного элемента статистической совокупности к абсолютной величине всей совокупности, т. е. как отношение части к общему (целому), и характеризует удельный вес части в целом, в форме процента. В анализе коммерческой деятельности торговли и сферы услуг относительные величины дают возможность изучить весь состав товарооборота по его ассортименту, состав работников фирмы – по определенным признакам (стажу работы, полу, возрасту), состав расходов предприятия и другие факторы, влияющие на коммерческую деятельность предприятия.

3. Относительные величины динамики характеризуют изменение изучаемого явления во времени, выявляют направление развития, измеряют интенсивность развития. Рассчитывается относительная величина динамики как отношение уровня признака в определенный период или момент времени к уровню того же признака в предшествующий период или момент времени, т. е. характеризует изменение уровня определенного явления во времени.

4. Относительные величины сравнения характеризуют количественное соотношение одноименных показателей, относящихся к различным объектам статистического наблюдения. Для сопоставления уровня цен на один и тот же товар, реализуемый через государственные магазины и на рынке, используются относительные величины сравнения. За базу сравнения принимается государственная цена.

5. Относительные величины координации – это разновидность показателей сравнения. Они применяются для характеристики соотношения между отдельными частями статистической совокупности. Относительные величины координации характеризуют структуру изучаемой совокупности.

6. Относительные величины интенсивности демонстрируют, насколько широко распространено исследуемое явление в определенной среде, характеризуются соотношением разноименных и взаимосвязанных между собой абсолютных величин.

Относительная величина демонстрирует, сколько единиц одной статистической совокупности приходится на единицу другой статистической совокупности.

Комплексное использование абсолютных и относительных величин дает всестороннюю характеристику изучаемого явления.

Относительные величины. Статистическое познание общества состоит не только в измерении уровней, достигнутых в развитии общественных явлений, но и в качественной оценке закономерностей развития, установлении взаимозависимости, что достигается путем сравнения и сопоставления. Результаты сопоставления выражаются при помощи относительных величин.

Относительными величинами называются обобщающие показатели, характеризующие количественные соотношения двух сопоставляемых статистических величин. Относительные величины имеют большое значение, без них нельзя обойтись в социально-экономическом анализе, т.к. абсолютные величины сами по себе не всегда позволяют дать правильную оценку исследуемого явления. Во многих случаях только в сравнении с другой величиной они проявляют истинную значимость.

Относительные величины широко используют в анализе, ими характеризуются структура, уровень удовлетворения общественных потребностей, развитие во времени. Имея большую устойчивость по сравнению с исходными данными, они широко применяются для прослеживания тенденций в развитии явлений. Основной особенностью относительных величин является то, что они дают возможность сравнивать такие общественные явления, абсолютные размеры которых непосредственно несопоставимы, в силу чего становится возможным сравнение уровня развития и распространенности общественных явлений.

Относительные величины образуются в результате сопоставления одноименных и разноименных статистических величин. В результате сопоставления одноименных величин получаются неименованные относительные величины. Они могут быть выражены в коэффициентах в виде кратного отношения, показывающего, во сколько раз данная величина больше или меньше той, с которой она сравнивается (т.е. база сравнения принимается за единицу). Широкой формой относительных величин являются проценты (%), при этом база сравнения принимается за 100.

В результате сравнения разноименных величин относительные показатели выражаются в единицах соответствующей размерности сочетания числителя и знаменателя сопоставлений (уровень производства отдельных видов продукции на человека, выраженный в кг на душу населения). Выбор формы выражения относительных величин зависит от задач исследования, характера исходных данных. Выбрать необходимо ту форму, которая легче воспринимается и наиболее наглядно выражает исследуемое соотношение.

Относительные статистические показатели, получаемые при сопоставлении абсолютных показателей, называются относительными показателями первого порядка, а при сопоставлении относительных – показателями высших (второго, третьего и т.д.) порядков.

Относительный показатель представляет результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов. Относительные величины вторичны по отношению к абсолютным показателям. Абсолютный показатель, находящийся в числителе, называется текущим или сравниваемым. Показатель, с которым производится сравнение и который находится в знаменателе, называется основанием или базой сравнения. Относительные показатели могут выражаться в коэффициентах, процентах и т.д.

Относительные показатели подразделяют на следующие виды:

Относительный показатель динамики (ОПД) представляет собой отношение уровня исследуемого процесса за данный период времени и уровня этого же процесса в прошлом:

Эта величина показывает, во сколько раз текущий уровень превышает базисный. Если данный показатель выражен кратным отношением, он называется коэффициентом роста, при домножении этого коэффициента на 100% получают темп роста.

Относительный показатель плана (ОПП) и реализации плана (ОПРП):

Между относительными показателями плана, реализации плана и динамики существует следующая взаимосвязь:

ОПД = ОПП . ОПРП

Относительный показатель структуры (ОПС) представляет собой соотношение структурных частей изучаемого объекта и их целого

Относительные показатели координации (ОПК) характеризуют соотношение отдельных частей целого между собой.

В качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной.

Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления в присущей ему среде:

Разновидностью относительных показателей являются относительные показатели уровня экономического развития, характеризующие производство продукции на душу населения.

Относительный показатель сравнения (ОПСр) представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, страны и т.п.):

Различают относительные величины простые (выполнение договорных обязательств, динамика, структура, пространственное сравнение, координация); составные (относительные величины интенсивности) и сложные (индексы).

Абсолютные и относительные величины характеризуют различные стороны: одни – размеры, другие – структуру, интенсивность, направленность, степень выполнения договорных обязательств. При их расчетах и использовании необходимо:

использовать достоверные, сопоставимые сравнительные величины по методике расчета, времени, территории;

вычислять обобщающие показатели на основе полных данных, а не случайных фактов;

применять для характеристики однородные явления;

выбирать правильно знаменатель, который должен быть типичным, а не случайным, т.к. он применяется в виде норматива;

использовать взаимосвязанные абсолютные и относительные величины.

Сравнение и сопоставление данных – неотъемлемая сторона статистического исследования. Эта задача решается при помощи относительных величин. Относительные величины получаются в результате деления двух показателей, один из которых является знаменателем, базой для сравнения. Таким образом, относительными величинами называются статистические показатели, выражающие количественные соотношения между явлениями общественной жизни Относительная величина показывает, во сколько раз сравниваемая величина больше или меньше базисной, или какую долю составляет по отношению ко второй, а в некоторых случаях сколько единиц одной величины приходится на единицу другой величины. Широко распространенной формой выражения относительных величин являются процентные отношения, при которых базисная величина принимается за 100. Часто относительные величины выражаются в форме промиллей, это означает, что основание принимается за 1000. Промилли обозначаются знаком о/оо. Если, например, относительная величина равна 18,2 промиллям, то это записывается так: 18,2 о/оо. Эта форма выражения относительных величин очень распространена в статистике населения, где рождаемость, смертность и др. показатели обычно выражаются в промиллях. Иногда при расчете относительных величин основание принимается за 10000, за 100  000, за 1 000 000.Так, часто на 10 000 жителей, рассчитывается число врачей, число больничных коек, число предприятий общественного питания, число посадочных мест в них.

Таблица 3.2. Связь между базой сравнения, формой выражения и обозначением относительных величин.

База сравнения	Форма выражения относительных величин	Обозначение полученных относительных величин
1	Коэффициент	Десятичная дробь
100	Процент	%
1000	Промилле	о/оо
10 000	Продецимилле	о/о оо

К промиллям, к отношениям, выражением на 10 000, 100 000 и т.п. прибегают для того, чтобы придать относительным величинам более удобней для восприятия вид, освободив их от очень дробных чисел, от большого числа знаков после занятий в десятичных дробях.

17. Относительная величина в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа.

По содержанию выражаемых количественных соотношений выделяют шесть видов относительных показателей: динамики, плана и выполнения плана, структуры, координации, интенсивности и уровня экономического развития, сравнения.

1. Относительный показатель динамики характеризует изменение изучаемого явления во времени и представляет собой соотношение показателей, характеризующих явление в текущем периоде и предшествующем (базисном) периоде.

Рассчитанный таким образом показатель называется коэффициентом роста (снижения). Он показывает, во сколько раз показатель текущего периода больше (меньше) показателя предшествующего (базисного) периода. Выраженный в %, относительный показатель динамики называется темпом роста (снижения).

2. Относительный показатель плана (прогноза) и выполнения плана. Относительный показатель плана (ОПП) и относительный показатель выполнения плана (ОПВП) используют все субъекты финансово-хозяйственной деятельности, осуществляющие текущее и стратегическое планирование. Они рассчитываются следующим образом:

Относительный показатель выполнения плана характеризует напряженность планового задания, а относительный показатель выполнения плана – степень его выполнения.

3. Относительные показатели структуры (ОПС) характеризуют доли (удельные веса) составных частей совокупности в общем ее объеме. Они показывают структуру совокупности, ее строение. Расчет относительных показателей структуры заключается в исчислении удельных весов отдельных частей во всей совокупности:

ОПС обычно выражаются в форме коэффициентов или процентах, сумма коэффициентов должна составлять 1, а сумма процентов – 100, так как удельные веса приведены к общему основанию.

Относительные показатели структуры используются при изучении состава сложных явлений, распадающихся на части, например: при изучении состава населения по различным признакам (возрасту, образованию, национальности и др.).

4. Относительные показатели координации (ОПК) характеризуют отношение частей данных статистической совокупности к одной из них, взятой за базу сравнения и показывают, во сколько раз одна часть совокупности больше другой, или сколько единиц одной части совокупности приходится на 1,10,100 и т.д. единиц другой части. За базу сравнения выбирается часть, имеющая наибольший удельный вес или являющаяся приоритетной в совокупности.

5. Относительные показатели интенсивности и уровня экономического развития (ОПИ)характеризуют степень распространения или уровень развития изучаемых явлений или процессов вопределённой среде и образуются как результат сравнения разноименных, но определенным образом связанных между собой величин. Указанные показатели рассчитываются следующим образом:

ОПИ исчисляются в расчете на 100, 1000, 1000 и т.д. единиц изучаемой совокупности и используются в тех случаях, когда невозможно по значению абсолютного показателя определить масштаб распространения явления. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности, естественного прироста (убыли) населения как отношение числа родившихся (умерших) или величины естественного прироста за год к среднегодовой численности населения данной территории на 1000 или 10 000 человек.

6. Относительные показатели сравнения (ОПСр) характеризуют сравнительные размеры одноименных абсолютных показателей, относящихся к различным объектам или территориям, но заодинаковый период времени. Их получают как частные от деления одноименных абсолютных показателей, характеризующих разные объекты, относящихся к одному и тому же периоду или моменту времени.

С помощью таких показателей сравнения можно сопоставлять производительность труда в разных странах и определять, где и во сколько раз она выше; сравнивать цены на различные товары, экономические показатели разных предприятий и т. д.

18. Средняя величина — это обобщающий показатель, характеризующий типический уровень явления в конкретных условиях места и времени. Он выражает величину признака, отнесенную к единице совокупности.

Массовые явления и процессы формируются под влиянием 2 групп причин:

1. общие причины для всех единиц – определяют состояние массового процесса и формируют типичный уровень; связаны с сущностью изучаемого явления;

2. индивидуальные причины – формируют специфические особенности отдельных единиц совокупности, их отклонение от типичного уровня. Эти причины не связаны с природой изучаемого явления.

Средняя всегда обобщает количественную вариацию признака, т. е. в средних величинах погашаются индивидуальные различия единиц, совокупности, обусловленные случайными обстоятельствами. Чем больше единиц совокупности берется для расчета средней, тем точнее средняя величина отражает типичный уровень или средняя является типичной.

В отличие от средней абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака единиц, относящихся к разным совокупностям. Таким образом, возникает необходимость расчета средней величины как обобщающей характеристики совокупности.

Так, если нужно сопоставить уровни оплаты труда работников на двух предприятиях, то нельзя сравнивать по данному признаку двух работников разных предприятий. Оплата труда выбранных для сравнения работников может быть не типичной для этих предприятий. Если же сравнивать размеры фондов оплаты труда на рассматриваемых предприятиях, то не учитывается численность работающих и, следовательно, нельзя определить, где уровень оплаты труда выше. В конечном итоге сравнить можно лишь средние показатели, т. е. сколько в среднем получает один работник на каждом предприятии.

Общие принципы применения средних величин:

1. Необходим обоснованный выбор единицы совокупности, для которой рассчитывается средняя;

2. При определении средней величины в каждом конкретном случае нужно исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков, а также имеющиеся для расчета данные;

3. Средняя величина должна прежде всего рассчитываться по однородной совокупности. Качественно однородные совокупности позволяет получить метод группировок, который всегда предполагает расчет системы обобщающих показателей.

4) Общие средние должны подкрепляться групповыми средними.

Средние величины делятся на два больших класса: 1) степенные средние: средняя геометрическая, средняя арифметическая, средняя квадратическая и средняя гармоническая; 2) структурные средние: мода и медиана.

Степенные средние в зависимости от представления исходных данных исчисляются в двух формах: простой и взвешенной.

Простая средняя считается по несгруппированным данным и. имеет следующий общий вид: 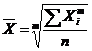  где Хi — варианта (значение) осредняемого признака; т — показатель степени средней; п — число вариант.

Взвешенная средняя считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения: 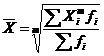  где Xi— варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта; т — показатель степени средней; f — частота, показывающая, сколько раз встречается i-е значение осредняемого признака.

Средние величины

Средней величиной в статистике называют обобщающий показатель, характеризующий общественное явление по одному количественному признаку (или типический размер признака данной совокупности).

Статистические средние – это реальные показатели, отражающие объективно существующие свойства общественных явлений (производительность труда, стоимость товара, урожайность, национальный доход на душу населения). Явления существуют в жизни, а статистикой характеризуются в виде определенных показателей.

Статистические средние отображают качественно определенные свойства общественных явлений. Этим они и отличаются от математических средних. Также отличительной особенностью средней является то, что в ней взаимно погашаются и уничтожаются индивидуальные отклонения различающихся между собой величин одного и того же вида. Она показывает значение признака для качественно однородной совокупности. Отсюда основным условием научного применения средней является расчет её по качественно однородным явлениям.

Средние величины, как и другие качественные обобщающие показатели, обладают относительной устойчивостью, что необходимо для выявления закономерностей. Лишь в достаточно большой совокупности случаев взаимно "погашаются" индивидуальные особенности каждого отдельного случая и более отчетливо обнаруживается то общее, что присуще всем единицам. Вычисление средней на основании слишком малого числа единиц сделает эту среднюю неустойчивой, ненадежной.

Сложность проблемы связана с необходимостью применения в разных случаях различных видов средних величин, с определением их содержания и экономического смысла.

Виды средних. При выборе способа и формулы для расчета средней величины необходим предварительный анализ взаимосвязи изучаемых явлений и определение статистической размерности изучаемой величины.

В статистике различают прямые и обратные величины, первичные и вторичные. Прямыми называются такие величины, значение которых увеличивается или уменьшается при увеличении или уменьшении характеризуемых ими явлений. Так, количество произведенной продукции в единицу рабочего времени является прямым показателем производительности труда, а трудоемкость – обратным. Так как статистическая размерность различна, то приходится применять в расчетах различные виды средних: арифметическую, гармоническую, геометрическую, квадратическую и другие, относящиеся к роду степенных средних.

Для расчета простых степенных средних применяется формула

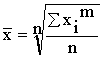
Взвешенные средние рассчитываются по формуле

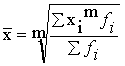
где   x_i – индивидуальное значение осредняемого признака, варианта;

 – среднее значение исследуемого явления;

m – показатель степени средней;

n – число единиц;

f _i – вес, частота.

Для первичных признаков применяются простые средние, для вторичных – взвешенные. Наиболее распространенной является средняя арифметическая простая, которая применяется в расчетах, когда единицы изучаемой совокупности представлены индивидуальными значениями признака (m=1):

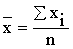
Средняя арифметическая взвешенная применяется в расчетах, когда индивидуальные значения определяемого признака имеют различную частоту повторения:

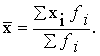
Когда отдельные варианты представлены в виде интервалов "от и до", в качестве варианта принимается середина интервалов. При наличии открытых интервалов границы их устанавливаются условно, исходя из конкретных условий задачи, или с учетом предыдущего интервала. При этом предполагается, что варианты внутри интервала распределяются равномерно. В действительности распределение вариантов внутри интервала может быть неравномерным и середина интервала может не совпадать со средней величиной в интервале. Но при большом числе единиц случайные отклонения взаимно погашаются и полученная средняя достаточно точно покажет типичный размер изучаемого признака.

5.2. Виды средних величин

В статистике используют различные виды средних величин, которые делятся на два больших класса:

• степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадра-тическая, средняя кубическая);

• структурные средние (мода, медиана).

Для вычисления степенных средних необходимо использовать все имеющиеся значения признака. Мода и медиана определяются лишь структурой распределения, поэтому их называют структурными, позиционными средними. Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.

Самый распространенный вид средней величины – средняя арифметическая. Под средней арифметической понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности. Вычисление данной величины сводится к суммированию всех значений варьирующего признака и делению полученной суммы на общее количество единиц совокупности. Например, пять рабочих выполняли заказ на изготовление деталей, при этом первый изготовил 5 деталей, второй – 7, третий – 4, четвертый – 10, пятый– 12. Поскольку в исходных данных значение каждого варианта встречалось только один раз, для опреде-

ления средней выработки одного рабочего следует применить формулу простой средней арифметической:

т. е. в нашем примере средняя выработка одного рабочего равна

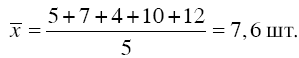
Наряду с простой средней арифметической изучают среднюю арифметическую взвешенную. Например, рассчитаем средний возраст студентов в группе из 20 человек, возраст которых варьируется от 18 до 22 лет, где xi – варианты осредняемого признака, fi – частота, которая показывает, сколько раз встречается i-е значение в совокупности (табл. 5.1).

Таблица 5.1

Средний возраст студентов

Применяя формулу средней арифметической взвешенной, получаем:

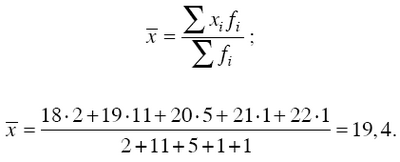
Для выбора средней арифметической взвешенной существует определенное правило: если имеется ряд данных по двум показателям, для одного из которых надо вычислить

среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя неизвестны, но могут быть найдены как произведение этих показателей, то средняя величина должна высчитывать-ся по формуле средней арифметической взвешенной.

В некоторых случаях характер исходных статистических данных таков, что расчет средней арифметической теряет смысл и единственным обобщающим показателем может служить только другой вид средней величины – средняя гармоническая. В настоящее время вычислительные свойства средней арифметической потеряли свою актуальность при расчете обобщающих статистических показателей в связи с повсеместным внедрением электронно-вычислительной техники. Большое практическое значение приобрела средняя гармоническая величина, которая тоже бывает простой и взвешенной. Если известны численные значения числителя логической формулы, а значения знаменателя неизвестны, но могут быть найдены как частное деление одного показателя на другой, то средняя величина вычисляется по формуле средней гармонической взвешенной.

Например, пусть известно, что автомобиль прошел первые 210 км со скоростью 70 км/ч, а оставшиеся 150 км со скоростью 75 км/ч. Определить среднюю скорость автомобиля на протяжении всего пути в 360 км, используя формулу средней арифметической, нельзя. Так как вариантами являются скорости на отдельных участках xj = 70 км/ч и Х2 = 75 км/ч, а весами (fi) считаются соответствующие отрезки пути, то произведения вариантов на веса не будут иметь ни физического, ни экономического смысла. В данном случае смысл приобретают частные от деления отрезков пути на соответствующие скорости (варианты xi), т. е. затраты времени на прохождение отдельных участков пути (fi/xi). Если отрезки пути обозначить через fi, то весь путь выразиться как ?fi, а время, затраченное на весь путь, – как ? fi/xi , Тогда средняя скорость может быть найдена как частное от деления всего пути на общие затраты времени:

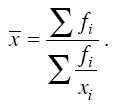
В нашем примере получим:

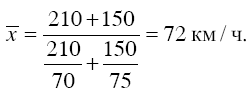
Если при использовании средней гармонической веса всех вариантов (f) равны, то вместо взвешенной можно использовать простую (невзвешенную) среднюю гармоническую:

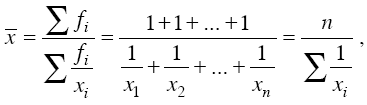
где xi – отдельные варианты; n – число вариантов осредняемого признака. В примере со скоростью простую среднюю гармоническую можно было бы применить, если бы были равны отрезки пути, пройденные с разной скоростью.

Любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялась величина некоторого итогового, обобщающего показателя, который связан с осредняемым показателем. Так, при замене фактических скоростей на отдельных отрезках пути их средней величиной (средней скоростью) не должно измениться общее расстояние.

Форма (формула) средней величины определяется характером (механизмом) взаимосвязи этого итогового показателя с осредняемым, поэтому итоговый показатель, величина которого не должна изменяться при замене вариантов их средней величиной, называется определяющим показателем. Для вывода формулы средней нужно составить и решить уравнение, используя взаимосвязь осредняемого показателя с определяющим. Это уравнение строится путем замены вариантов осредняемого признака (показателя) их средней величиной.

Кроме средней арифметической и средней гармонической в статистике используются и другие виды (формы) средней величины. Все они являются частными случаямистепенной средней. Если рассчитывать все виды степенных средних величин для одних и тех же данных, то значения

их окажутся одинаковыми, здесь действует правило мажо-рантности средних. С увеличением показателя степени средних увеличивается и сама средняя величина. Наиболее часто применяемые в практических исследованиях формулы вычисления различных видов степенных средних величин представлены в табл. 5.2.

Таблица 5.2

Виды степенных средних

Средняя геометрическая применяется, когда имеется n коэффициентов роста, при этом индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики. Средняя характеризует, таким образом, средний коэффициент роста. Средняя геометрическая простая рассчитывается по формуле

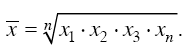
Формула средней геометрической взвешенной имеет следующий вид:

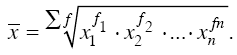
Приведенные формулы идентичны, но одна применяется при текущих коэффициентах или темпах роста, а вторая – при абсолютных значениях уровней ряда.

Средняя квадратическая применяется при расчете с величинами квадратных функций, используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения и вычисляется по формуле

Средняя квадратическая взвешенная рассчитывается по другой формуле:

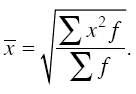
Средняя кубическая применяется при расчете с величинами кубических функций и вычисляется по формуле

средняя кубическая взвешенная:

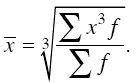
Все рассмотренные выше средние величины могут быть представлены в виде общей формулы:

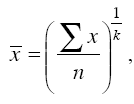
где – средняя величина; – индивидуальное значение; n – число единиц изучаемой совокупности; k – показатель степени, определяющий вид средней.

При использовании одних и тех же исходных данных, чем больше k в общей формуле степенной средней, тем больше средняя величина. Из этого следует, что между величинами степенных средних существует закономерное соотношение:

Средние величины, описанные выше, дают обобщенное представление об изучаемой совокупности и с этой точки зрения их теоретическое, прикладное и познавательное значение бесспорно. Но бывает, что величина средней не совпадает ни с одним из реально существующих вариантов, поэтому кроме рассмотренных средних в статистическом анализе целесообразно использовать величины конкретных вариантов, занимающие в упорядоченном (ранжированном) ряду значений признака вполне определенное положение. Среди таких величин наиболее употребительными являются структурные, или описательные, средние – мода (Мо) и медиана (Ме).

Мода – величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда, т. е. вариант, обладающий наибольшей частотой. Мода может применяться при определении магазинов, которые чаще посещаются, наиболее распространенной цены на какой-либо товар. Она показывает размер признака, свойственный значительной части совокупности, и определяется по формуле

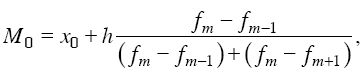
где х0 – нижняя граница интервала; h – величина интервала; fm – частота интервала; fm_1 – частота предшествующего интервала; fm+1 – частота следующего интервала.

Медианой называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности. При этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой – больше ее. Медиана используется при изучении элемента, значение которого больше или равно или одновременно меньше или равно половине элементов ряда распределения. Медиана дает общее представление о том, где сосредоточены значения признака, иными словами, где находится их центр.

Описательный характер медианы проявляется в том, что она характеризует количественную границу значений варьирующего признака, которыми обладает половина единиц совокупности. Задача нахождения медианы для дискретного вариационного ряда решается просто. Если всем единицам ряда придать порядковые номера, то порядковый номер медианного варианта определяется как (п +1) / 2 с нечетным числом членов п. Если же количество членов ряда является четным числом, то медианой будет являться среднее значение двух вариантов, имеющих порядковые номера n / 2 и n / 2 + 1.

При определении медианы в интервальных вариационных рядах сначала определяется интервал, в котором она находится (медианный интервал). Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех частот ряда. Расчет медианы интервального вариационного ряда производится по формуле

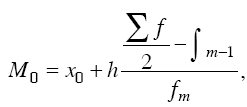
где X0 – нижняя граница интервала; h – величина интервала; fm – частота интервала; f– число членов ряда;

?m-1 – сумма накопленных членов ряда, предшествующих данному.

Наряду с медианой для более полной характеристики структуры изучаемой совокупности применяют и другие значения вариантов, занимающих в ранжированном ряду вполне определенное положение. К ним относятся квартили и децили. Квартили делят ряд по сумме частот на 4 равные части, а децили – на 10 равных частей. Квартилей насчитывается три, а децилей – девять.

Медиана и мода в отличие от средней арифметической не погашают индивидуальных различий в значениях варьирующего признака и поэтому являются дополнительными и очень важными характеристиками статистической совокупности. На практике они часто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содержит некоторое количество единиц с очень большим или очень малым значением варьирующего признака. Эти, не очень характерные для совокупности значения вариантов, влияя на величину средней арифметической, не влияют на значения медианы и моды, что делает последние очень ценными для экономико-статистического анализа показателями.