Ортогональные представления сигналов
При анализе прохождения сложного сигнала s(t) через линейную систему (идеальная система, у которой зависимость Uвых от Uвх строго линейна) сигнал представляют в виде [5]
(2.3)
где k(t) - базисные функции;
Ck - безразмерные коэффициенты.
Если базисные функции (базис) заданы, то s(t) полностью определяется коэффициентами Ck, совокупность которых называют обобщённым дискретным спектром сигнала s(t).
За пределами интервала [t1,t2] сигнал (2.3) считается условно продолжающимся, что может оказаться неприемлемым для представления сигналов конечной длительности.
Для представления ограниченного во времени сигнала применяется интеграл
,
(2.4)
где (,t) - базисная функция непрерывного аргумента ;
S() - спектральная плотность, описывающая непрерывный, сплошной спектр.
Сравнивая выражения (2.3) и (2.4), можно отметить, что S()d - аналог безразмерного коэффициента Ck.
Совокупность методов представления в виде (2.3) и (2.4) называется обобщенной спектральной теорией сигналов.
Требования к базисным функциям.
1. Простое аналитическое выражение.
2. Быстрая сходимость ряда (2.3).
3. Простота вычисления коэффициентов Ck.
4. Простота технической реализции.
Этим требованиям отвечают ортогональные базисные функции, удовлетворяющие условию:
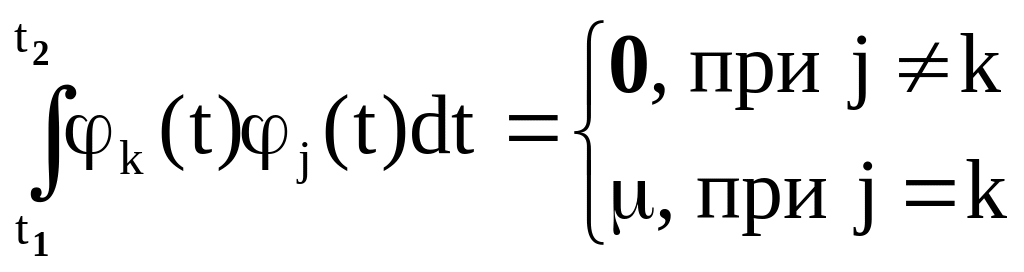. (2.5)
При умножении всех
функций i(t),
i=
на
,
система функций i(t)
будет ортонормированной
(ортонормальной) и
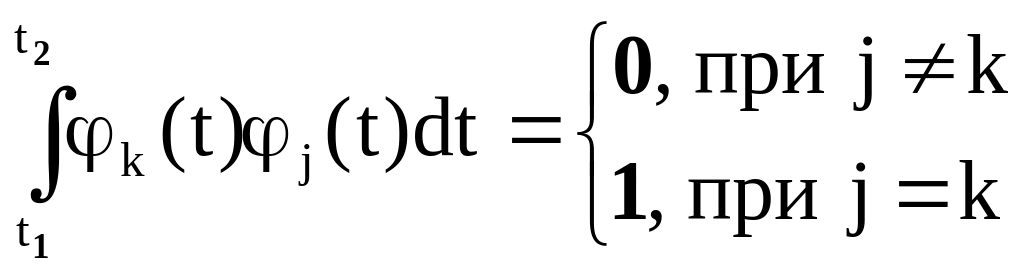. (2.6)
Вернемся к представлению (2.3) в случае ортогональности i(t).
Умножим правую и левую от знака равенства части выражения (2.3) на j(t) и проинтегрируем на отрезке [t1,t2], лежащем внутри интервала ортогональности [a,b].
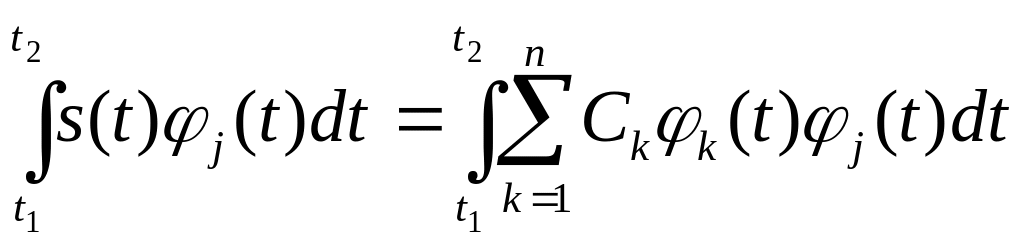
или
.
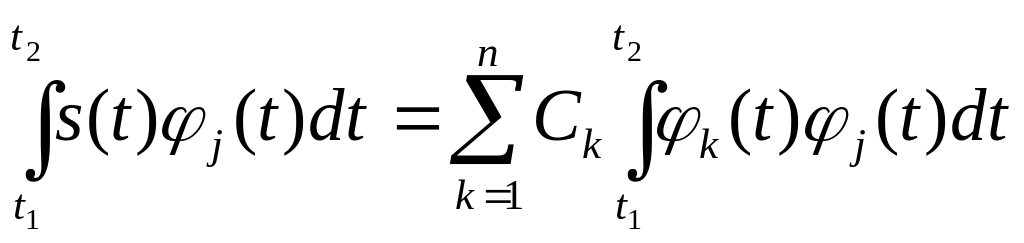При jk все интегралы в правой части этого выражения равны 0, а при j=k равны 1 (в соответствии с (2.6)). Следовательно,
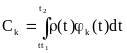. (2.7)
Важное свойство - сходимость ряда (2.3) к функции s(t). Для оценки этой сходимости используют различные критерии.
При среднеквадратической сходимости оценку осуществляют по критерию
. (2.8)
Примеры ортогональных систем
Система тригонометрических функций
ортонормированна на
отрезке [-,],
при переходе к
имеет вид
(ортонормированна на
отрезке
).
Система показательных функций
; k=-,...,-2,-1,0,1,2,...,
также ортонормированна на отрезке [-,].
3. Полиномы Лежандра ортогональны на [-1,1]
0(t)=1; 1(t)=t; 2(t)= 3(t)=
|
Нормированные функции Лежандрa
|
;
;
.
.Полиномы Лежандра ортонормальны с весом e-t на интервале (0,),
0(t)=1; |
1(t)=-t+1; |
2(t)= |
n(t)= |
;
.
4.Полиномы Чебышева
ортогональны на интервале [1,-1] с весом
.
0(t)= 1(t)= 2(t)= 3(t)=
n(t)=
|
Полиномы Чебышева удовлетворяют условию наилучшей аппроксимации в среднеквадратической метрике на системе равноотстоящих точек. |
|
|
5.Полиномы Эрмита,
ортонормированы на [-,]
c весом
|
|
0(t)= 1(t)= 2(t)= 3(t)= n(t)= |
|
;
;
;
;
.
;
;
;
;
.