Лекция 6 модуляторы

Угловая модуляция. Дискретная амплитудная модуляция (ДАМ). Дискретная фазовая модуляция (ДФМ). Дискретная частотная модуляция (ДЧМ). Импульсные виды модуляции. Модуляция случайными сигналами

Угловая модуляция

Как правило, ФМ и ЧМ объединяются в угловую модуляцию.

Девиация частоты () - абсолютное максимальное изменение частоты.

Закон изменения частоты (рис.6.1):

,

.

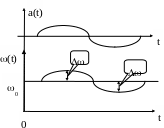
Рис.6.1Изменение частоты при частотной модуляции

Q(t) - мгновенный угол.

При частотной модуляции мгновенный угол (фаза) будет иметь вид

(6.1)

где _чм  индекс частотной модуляции.

В этом виде модуляции индекс _чм зависит от частоты модулирующего колебания.

При фазовой модуляции

, (если ).

, (6.2)

где _фм  индекс фазовой модуляции.

По сравнению с частотной модуляцией _фм не зависит от частоты модулирующего колебания.

Так как:

;

;

.

где - функция Бесселя первого рода n-го порядка от аргумента . После выполнения несложных преобразований, получим

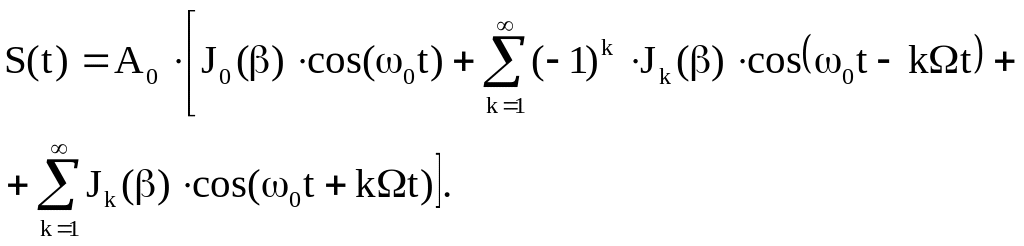(6.3)

Замечания к этому выражению.

1. Формула получена без применения прямого интегрального преобразования Фурье.

2. Спектр состоит из 3-х частей:

1-е слагаемое - несущее колебание с амплитудой, определяемой функцией Бесселя J₀();

2-е слагаемое - бесконечное количество разностных частотных продуктов;

3-е слагаемое - бесконечное количество суммарных частотных продуктов.

Даже в идеальном случае спектр бесконечен. С ростом k амплитуда быстро убывает.

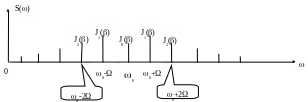
Пример спектра сигнала с угловой модуляцией приведён на рис.6.2.

Рис.6.2Спектр сигнала угловой модуляции

Оценим ширину спектра S.

Если :

 при ЧМ (ширина спектра не зависит от );

 при ФМ (ширина спектра зависит от частоты сигнала ).

При , ,

Дискретная амплитудная модуляция (дам)

Информационный a(t)запишем в виде бесконечного ряда

Модулированный сигнал будет иметь вид

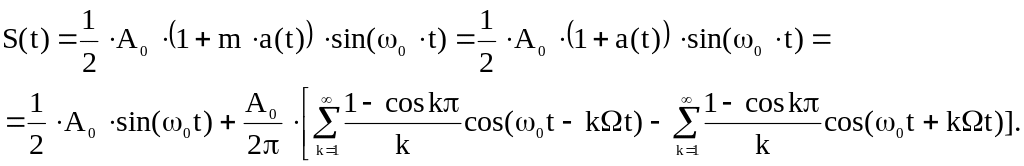(6.4)

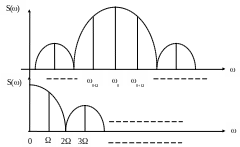Формирование спектра сигнала ДАМ представлено на рис.6.3.

Рис.6.3Спектр сигнала дискретной амплитудной модуляции

Спектр сигнала ДАМ можно получить с помощью переноса спектра модули-рующего сигнала a(t) по оси частот вправо и добавления слева от несущего колебания зеркального отражения этого спектра сигнала модулирующего.

Дискретная фазовая модуляция (дфм)

При ДФМ сигнал S(t) может быть записан в виде

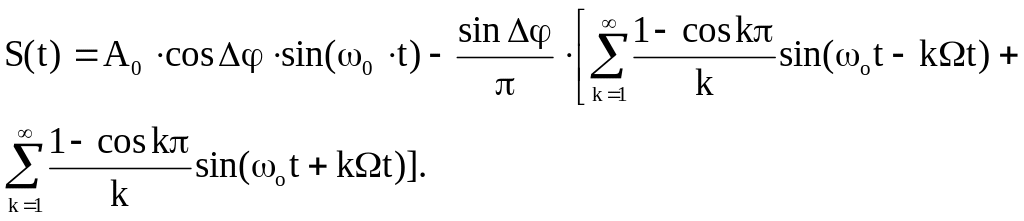(6.5)

На рис. 5.4 приведены диаграммы спектров сигнала ДФМ для различных индексов модуляции.

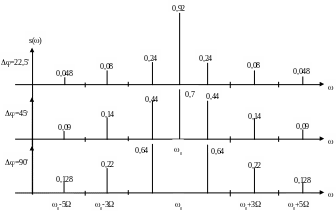
Рис.6.4Спектры сигналов фазовой манипуляции при различных значениях 

Дискретная частотная модуляция (дчм).

Существуют две разновидности сигналов частотной модуляции:

1. ДЧМ с разрывом фазы.

2. ДЧМ без разрыва фазы.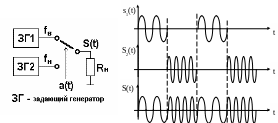

Спектр сигнала ДЧМ с разрывом фазы получается путём совмещения спектров ДАМ (рис.5.3) с несущими колебаниями на частотах f_в и f_н (рис.6.5).

Рис.6.5Структурная схема и временные диаграммы формирования

сигнала ЧМ с разрывом фазы

Рассмотрим формирование спектра при ДЧМ без разрыва фазы (рис.6.6).

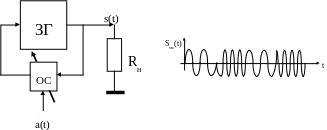
Рис.6.6Структурная схема и временная диаграмма формирования

сигнала ЧМ без разрыва фазы

Для сокращения вычислений при определении спектрального состава сигнала ДЧМ без разрыва фазы запишем его в комплексной форме

, (6.6)

где

. (6.7)

Графики изменения частоты (t) и фазы (t) при частотной манипуляции показаны на рис.6.7. Поскольку (t) является периодической функцией, то и e^i(t) также периодическая и может быть разложена в ряд Фурье

,

где .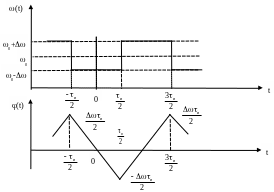

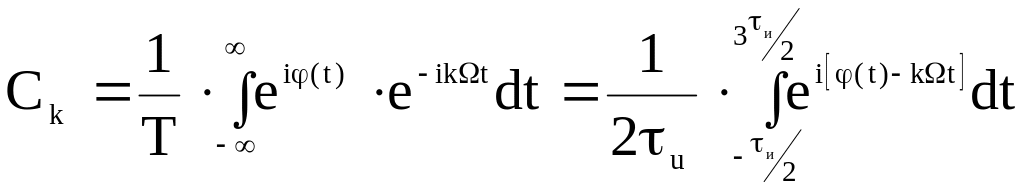Рис.6.7Изменение частоты и фазы при частотной манипуляции

Производя интегрирование с учётом (5.6), получим

.

Взяв действительную часть сигнала s(t), находим сигнал ДЧМ2

(6.7)

На рис.5.8 показаны рассчитанные по этой формуле спектры сигналов ДЧМ при различных значениях .

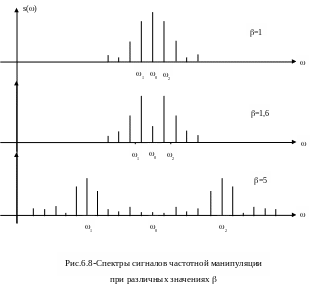
При малых индексах модуляции , спектральные линии группируются вблизи (несущей частоты), при этом амплитуда спектральных составляющих убывает пропорционально .

При нецелых индексах модуляции, спектральных линий на частотах манипуляции f_в и f_н не наблюдается (они располагаются ниже или выше частот f_в и f_н ), хотя эти частоты существуют.

При больших , спектр похож на ДЧМ1.