7. Корреляционный анализ

Корреляционный анализ изучается во многих дисциплинах: математическая статистика, статистика, но у студентов встречаются пробелы, связанные с графическим представлением связи переменных, предпосылками корреляционного анализа и типами ложной корреляции.

Корреляционный анализ получил широкое применение по двум его показателям качества:

- простота расчета коэффициента корреляции и его достоверности;

- четкость в интерпретации тесноты связи между переменными.

Однако, среди исследователей очень распространено использование ложного коэффициента корреляции.

Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными.

Допустим имеется два массива чисел двух переменных Х и У для определенных объектов исследований.

Коэффициент корреляции вычисляется по выборке совместных наблюдений величин Х и У по формуле:

где Х_i , У_i – значения переменных;

i – порядковый номер значения переменных;

Х_с, У_с – средние значения переменных.

Формула коэффициента корреляции читается следующим образом: коэффициент корреляции между переменными Х и У равен частному от деления числителя на знаменатель.

Числитель равен сумме произведений отклонений Х и У от своих средних значений.

Знаменатель равен корню квадратному от произведения суммы квадратов отклонений Х и У от своих средних значений.

Умение правильно прочитать математическую формулу входит в состав общекультурных компетенций.

Коэффициент корреляции обладает следующими свойствами:

1. Значения коэффициента корреляции r(Х,У) могут находиться в интервале [-1,+1].

2. Отрицательное значение r(Х,У) означает, что при увеличении Х наблюдается тенденция уменьшения У.

3. Положительное значение r(Х,У) означает, что при увеличении Х наблюдается увеличение У.

4. Если между Х и У существует функциональная линейная зависимость, то коэффициент корреляции принимает значения либо +1, либо -1.

5. Если коэффициент корреляции равен 0, то это означает, что между Х и У нет линейной зависимости, но может быть нелинейная зависимость.

Допустим имеется два массива чисел Х и У

Построим корреляционное поле зависимости У от Х см. рис. 4.

Рис. 4 – Корреляционное поле зависимости У от Х

Разделим корреляционное поле двумя линиями У_с и Х_с, которые выделят четыре зоны.

Выделенные зоны обладают следующими свойствами:

- в первой зоне произведения отклонений (Х_i-Х_с)*(У_i-У_с) имеют положительные значения, так как отклонения имеют одинаковый положительный знак;

- в третьей зоне отклонения (Х_i-Х_с) и (У_i-У_с) имеют одинаковый отрицательный знак, а их произведение (Х_i-Х_с)*(У_i-У_с) имеет положительное значение;

- во второй и четвертой зоне отклонения (Х_i-Х_с) и (У_i-У_с) имеют разные знаки, а их произведения имеют отрицательное значение.

∑(Х_i-Х_с)* (У_i-У_с) - сумма произведений отклонений значений Х и У от своих средних значений, обладает следующими свойствами:

- будет иметь положительное значение, если исходных данных будет больше в третье и первой зоне (данные будут иметь прямо пропорциональную или положительную тенденцию),

- будет отрицательной, если исходных данных будет больше во второй и четвертой зоне (данные будут иметь обратно пропорциональную или отрицательную тенденцию)

- будет равной нулю, если исходных данных будет одинаково во всех зонах (данные будут расположены по кругу и линия тенденции будет иметь горизонтальную линию, совпадающей с У_с).

От знака числителя коэффициента корреляции ∑(Х_i-Х_с)*(У_i-У_с) зависит знак коэффициента корреляции, так как знаменатель коэффициента корреляции всегда будет положительным числом.

На рисунке 5 показаны примеры исходных корреляционных полей и рассчитанных для них коэффициентов корреляции

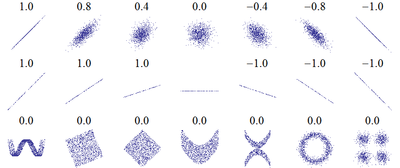
Рис. 5 – Примеры исходных корреляционных полей и рассчитанных для них коэффициентов корреляции

Анализ рис. 5 показывает следующее;

- на первой строке коэффициент корреляции отражает «зашумлённость» линейной зависимости и характеризует степень связи между двумя переменными от +1 до -1,

- на второй строке знак коэффициента корреляции характеризует наклон строго функциональной линейной зависимости,

- на третьей строке показаны примеры исходных данных, при которых коэффициент корреляции равен нулю, так как количество данных в четырех зонах является одинаковым.