4. Графическое представление массива чисел
Массив может содержать больше 9 чисел, которые нельзя запомнить (см. свойства информации 3Д, число Миллера), поэтому для визуализации массива чисел используются графические средства.
На примере построения гистограммы продемонстрируем вычислительные средства, которые используются в эконометрике: графические средства Ехсе1, функция Ехсе1 «частота», программные средства Ехсе1 «Анализ данных», пакет прикладных программ Stadia 8.
Самым простым и наиболее распространенным средством графического представления массива чисел является гистограмма, в которой по оси Х откладывается порядковый номер массива чисел по оси У откладываются численные значения массива чисел см. рис. 1.
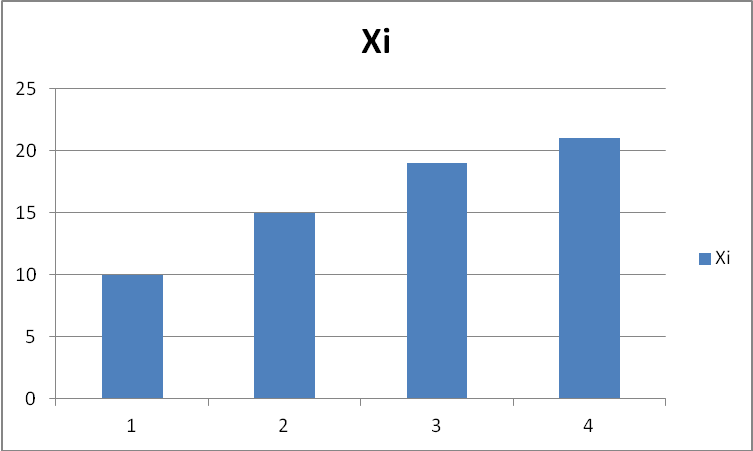
Рис. 1 – гистограмма массива чисел
Приводим скриншоты построения гистограммы средствами Ехсе1.
Шаг 1. Копируем данные и вставляем в лист Ехсе1 или вводим данные в лист Ехсе1
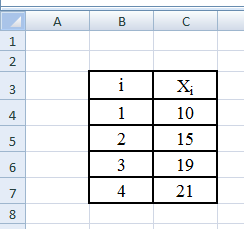
Шаг 2. Выделяем колонку значений Хi
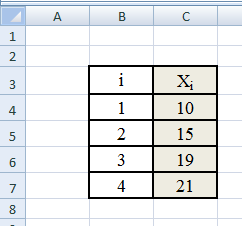
Шаг 3. Вставка, гистограмма.
Если количество чисел в массиве больше 9, то составляется группировка чисел, затем строится гистограмма, где по оси Х откладывается номер группы, по оси У откладывается количество чисел в группе, полученный график называется полигоном распределения массива чисел см. рис. 2.
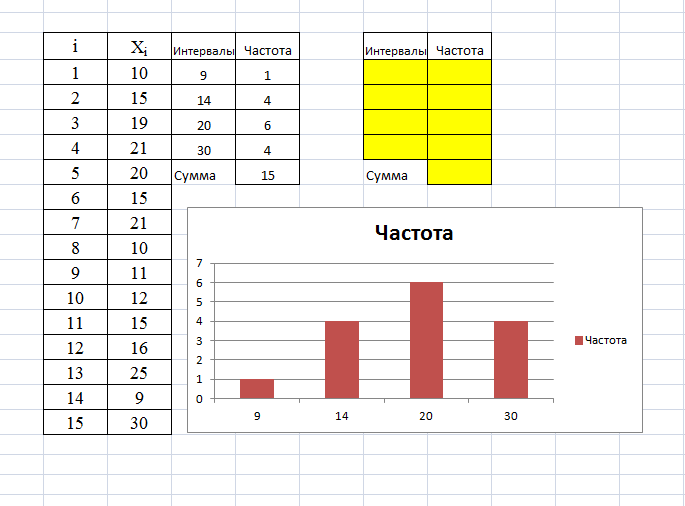
Рис. 2 – Полигон распределения частот
Поясним содержание рис. 2.
В колонках i и Хi находятся исходные данные в количестве 15 штук.
Колонка «Интервалы» содержит четыре интервала:
- первый интервал, равный минимальному значению массива чисел, будет включать числа, которые меньше или равны 9,
- второй интервал будет включать числа, которые меньше 9, но больше или равные 14;
- третий интервал будет включать числа меньше 14, но большие или равные 20
- последний интервал (30), равный максимальному значению массива чисел, будут включать числа больше или равные 30.
Для определения минимального числа массива можно использовать функцию: =МИН(C19:C33),
где C19:C33 диапазон массива чисел.
Для определения максимального числа массива можно использовать функцию: =МАКС(C19:C33)
Колонка «Частота» содержит матричную функцию:
{=ЧАСТОТА(C19:C33;D19:D22)},
где C19:C33 – диапазон массива чисел,
D19:D22 – диапазон интервалов.
Покажем скриншоты выполнения матричной функции «Частота».
Шаг 1: вводим ячейку Е19 функцию «Частота»: =, f(x), категория – статистические, частота, ОК
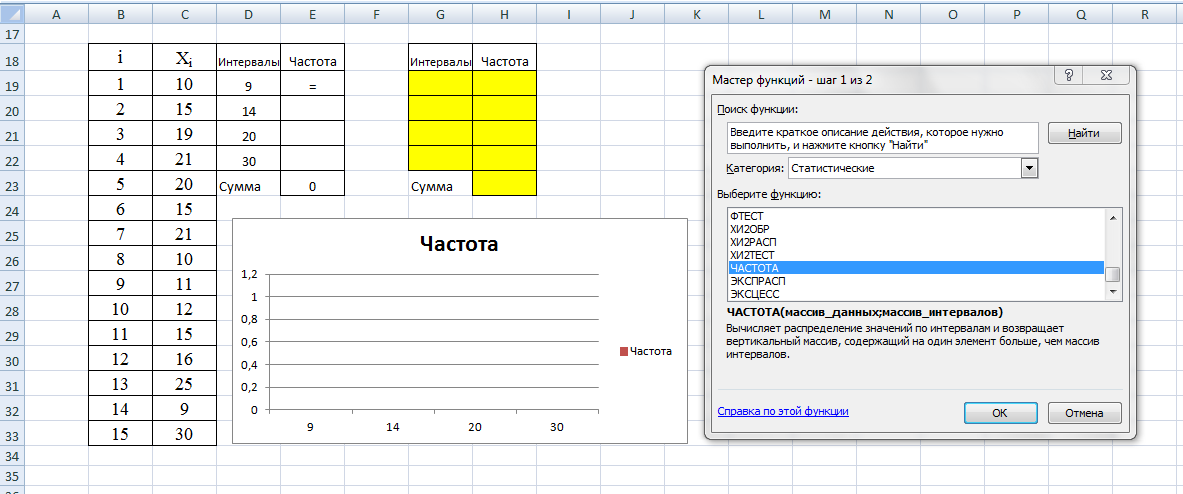
Шаг 2. Указываем диапазон данных, указываем диапазон интервалов.
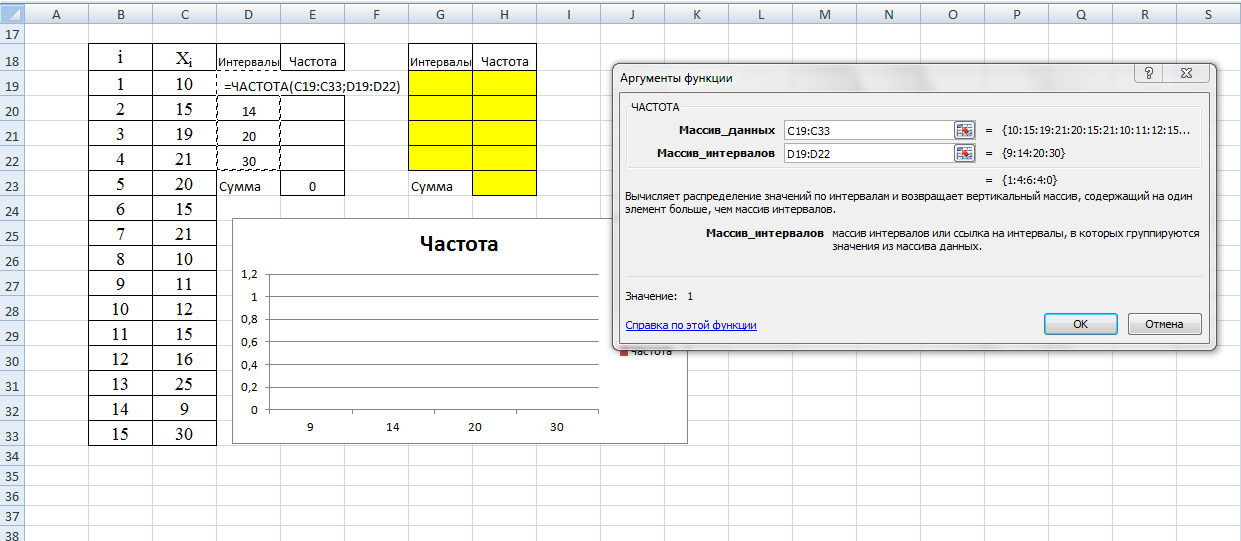
Шаг 3. ОК
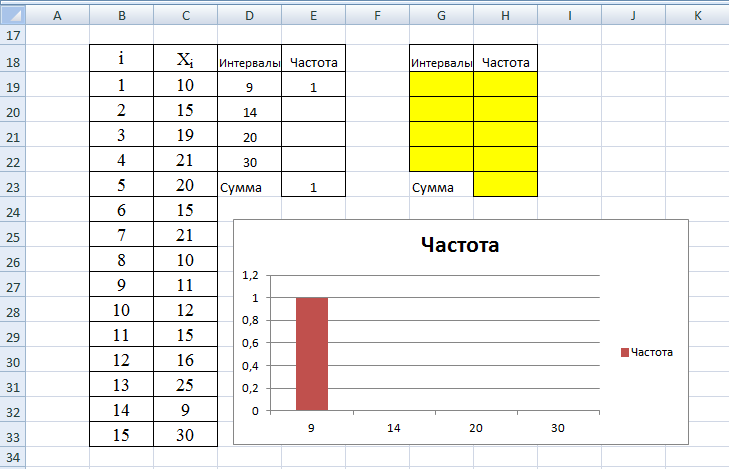
На третьем шаге была введена функция «Частота», которая имеет следующий вид:
=ЧАСТОТА(C19:C33;D19:D22)
Однако она не стала еще матричной, так как она не имеет фигурных скобок.
Шаг 4. Преобразование функции частота в матричную:
Шаг 4.1. Выделяем ячейки, на которые должна распространяться матричная функция. Обращаем Ваше внимание, что выделяем ячейки, а не переносим или автозаполняем.
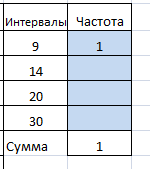
Шаг 4.2. Нажимаем клавишу F2;
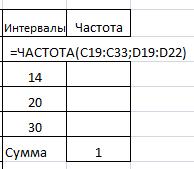
Шаг 4.3
- последовательно нажимаем, не отпуская, клавиши: Ctr, Shift, Enter;
- одновременно отпускаем все клавиши.
Содержимое одной из ячеек матричной функции имеет вид
Обратите внимание, что матричная функция имеет фигурные скобки.
Ячейки, в которых находится матричная функция, нельзя по отдельности удалять. Можно удалить содержимое всех ячеек матричной функции.
Правила ввода матричных функций необходимо запомнить, так как они являются общими для всех матричных функций, особенно для таких матричных функций: ТРАНСП, МОБР, МУМНОЖ, ЛИНЕЙН, которые мы будем часто использовать в расчетах, особенно матричную функцию ЛИНЕЙН.
Обращаем Ваше внимание на наличие в скриншотах ячеек, выделенных желтым цветом.
В ячейках выделенных желтым цветом необходимо повторить расчеты и сравнить с исходными результатами расчетов, если возникают различия, то необходимо найти ошибку.
Повторение расчетов в выделенных желтым цветом ячейках является дидактическим приемом, который будет использован в расчетах по всем лабораторным работам. Данный дидактический прием позволяет перевести полученную информацию в знания и умения. Навыки появятся, если студенты будут выполнять эти операции автоматически. Компетенции появятся, если студенты смогут с помощью этих операций выполнить проведение расчетов для различных объектов исследования.
Полигон распределения частот можно получить с помощью разных программных средств.