23. Описание расчетов

Для того, чтобы описание расчетов обладало свойством 3Д, оно должно иметь следующую структуру:

1) постановка задачи;

2) таблица исходных данных;

3) график зависимости У от Х

4) протокол расчетов;

5) запись математической модели и ее характеристик;

6) анализ характеристик модели;

7) выводы в соответствии с постановкой задачи.

Приводим пример описания расчетов.

1) Постановка задачи.

Имеется предположение, что предложение на товар зависит от его спроса. Необходимо проверь это предположение на конкретных товарах.

2) Таблица данных.

Для решения задачи было обследовано шесть магазинов, в которых определялись предложение и спрос на товары бытовой химии в течение одного месяца в 2013 году.

Предложение равнялось сумме стоимости товаров бытовой химии, поступивших в магазин в течение месяца.

Спрос равнялся месячному товарообороту товаров бытовой химии.

В таблице 9 представлены данные спроса и предложения на товары бытовой химии в течение месяца в 2013 году в городе N.

Таблица 9 – спрос и предложение на товары бытовой химии

i	Х1i	Уi
1	12	15
2	13	16
3	15	18
4	16	20
5	14	17
6	21	26

где Х – спрос на товар (тыс. руб.);

У – предложение на товар (тыс. руб.);

i – номер магазина.

3) График зависимости У от Х

Построим график зависимости У от Х и определим вид тенденции этой зависимости.

На рис. 9 показано корреляционное поле зависимости У от Х

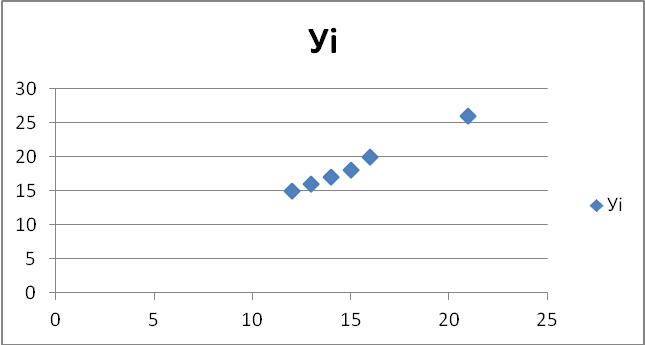
Рис. 9 – Корреляционное поле зависимости У от Х

Визуальный анализ зависимости У от Х показывает, что с ростом Х увеличивается У и эта тенденция имеет линейный вид.

Можно рассчитать коэффициент корреляции, который подтвердить наше утверждение, но в этом нет необходимости.

Вычислим основные характеристики линейной модели

У_i = а₀+а₁*Х_i+е_i с помощью матричной функции Ехсе1 «Линейн».

4) Протокол расчетов.

Приводим протокол расчетов по функции «Линейн» см. рис. 10.

1,245901639	-0,229508197
0,045784394	0,707068774
0,994627359	0,326431275
740,5128205	4
78,90710383	0,426229508

Рис. 10 – Протокол проведения расчетов по функции «Линейн»

5) Запись математической модели и ее характеристик

Приводим характеристики эконометрической модели с использованием протокола расчетов по функции «Линейн».

У = -0,229 + 1,245*Х + е (линейная регрессионная модель)

0,707 0,045 (ошибки коэффициентов модели)

R² = 0,99 (коэффициент детерминации)

Е = 0,32 (ошибка модели)

F = 740,51 (критерий Фишера);

n = 6 – объем выборки;

k = 2 – число всех коэффициентов в модели;

(n-k) = 4 (число степеней свободы для остатков)

C_рег = 78,9071 (вариация для регрессии)

С_ост = 0,42623 (вариация для остатков)