21. Точечный и интервальный прогноз
Методологической основой прогнозирования являются инерционные свойства экономической системы. В настоящем присутствуют элементы прошлого и зачатки будущего.
Прогнозирование в эконометрических исследованиях производится по регрессионным моделям.
Точечный прогноз- это среднее значение прогнозной переменной, которое вычисляется по формуле:
Упр = а0+а1*Хож,
где Упр - прогнозное значение зависимой переменной на ожидаемый период,
Хож - численное значение объясняемой переменной на ожидаемый период.
Интервальный прогноз - это интервал, в котором с определенной вероятностью может находиться фактическое значение прогнозной величины.
Существуют два вида интервальных прогнозов: для индивидуальных значений и для математических ожиданий.
С вероятность 1- можно утверждать, что индивидуальное значение прогноза будет находиться в интервале
от Упр - Ош.пр.и.
до Упр + Ош.пр.и.,
где Ош.пр.и. - ошибка прогноза для индивидуальных значений зависимой переменной,
t - критерий Стьюдента на уровне значимости и числе степеней свободы k,
(альфа) - уровень значимости, равный вероятности совершить ошибку при отклонении нулевой гипотезы,
n - объем выборки,
k - количество всех коэффициентов в уравнении регрессии,
Е - ошибка модели,
Хi - текущее значение объясняемой переменной,
Хс - среднее значение объясняемой переменной,
Хож - ожидаемое значение объясняемой переменной.
Ошибка прогноза для индивидуальных значений обладает следующими свойствами:
Свойство 1. Чем дальше находится Хож от Хс, тем больше прогнозный доверительный интервал.
Свойство 2. Чем больше ошибка модели Е, тем больше прогнозный доверительный интервал.
Свойство 3. Чем меньше , тем больше t, тем больше прогнозный доверительный интервал.
Свойство 4. Чем больше n, тем меньше прогнозный доверительный интервал,
Свойство 5. Чем больше вариация Х, тем меньше прогнозный доверительный интервал.
Вывод. Для того, чтобы уменьшить прогнозный доверительный интервал для индивидуальных значений зависимой переменной, необходимо улучшить спецификацию модели, увеличить объем выборки, увеличить дисперсию объясняемой переменной.
С вероятность 1- можно утверждать, что прогнозное значение математического ожидания зависимой переменной будет находиться в интервале
от Упр - Ош.пр.м.
до Упр + Ош.пр.м.,
где
Ош.пр.м. - ошибка прогноза для математического ожидания зависимой переменной.
П
риводим
основные элементы графика регрессионного
уравнения, см. рис. 8.
Рис. 8 – Основные элементы графика регрессионного уравнения
22. Вычислительные средства расчетов основных характеристик линейной модели
Вычислительные средства Ехсе1.
С помощью матричной функции ЛИНЕЙН можно рассчитать основные характеристики линейной модели.
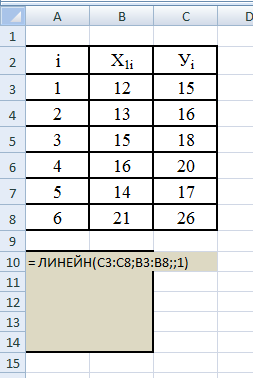
Протокол расчетов линейной модели Уi = а0+а1*Хi+еi, с помощью матричной функции ЛИНЕЙН имеет следующий вид:
а1 |
а0 |
Sa1 |
Sa0 |
R2 |
E |
F |
n-k |
Cрег |
Сост |
где
- коэффициент а1
a0= Уc - a1*Хc - коэффициент а0
Sа0 - ошибка коэффициента а0,
Sa1 - ошибка коэффициента а1.
- коэффициент детерминации
- ошибка модели
- критерий Фишера
где S2рег = Cрег/(k-1) = - дисперсия регрессии.
S 2оcт = Cост/(n-k) = - дисперсия остатков,
- вариация регрессии
- вариация остатков
(n-k) - число степеней остатков
n – объем выборки
k – количество всех коэффициентов в модели.
Пример расчетов основных характеристик модели с помощью матричной функции «Линейн».
Имеются данные, представленные в таблице 8.
Таблица 8 – Исходные данные спроса и предложения на товар
i |
Х1i |
Уi |
1 |
12 |
15 |
2 |
13 |
16 |
3 |
15 |
18 |
4 |
16 |
20 |
5 |
14 |
17 |
6 |
21 |
26 |
где Х – спрос на товар (тыс. руб.)
У – предложение на товар (тыс. руб.)
i – номер магазина.
Необходимо вычислить основные характеристики линейной модели
Уi = а0+а1*Хi+еi с помощью матричной функции Ехсе1 «Линейн».
Решение.
Шаг 1.
Копируем таблицу 8 с данными и вставляем ее в лист Ехсе1.
Шаг 2.
Вводим функцию Линейн.
= , f(х), категория «Статистические», функция «Линейн»,
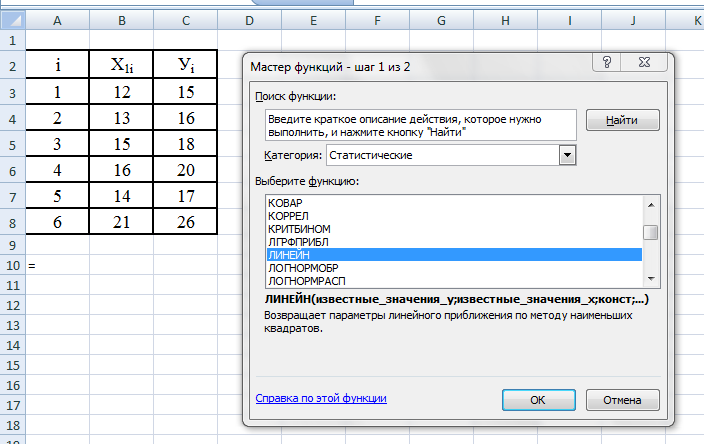
Шаг 3. Вводим параметры функции Линейн
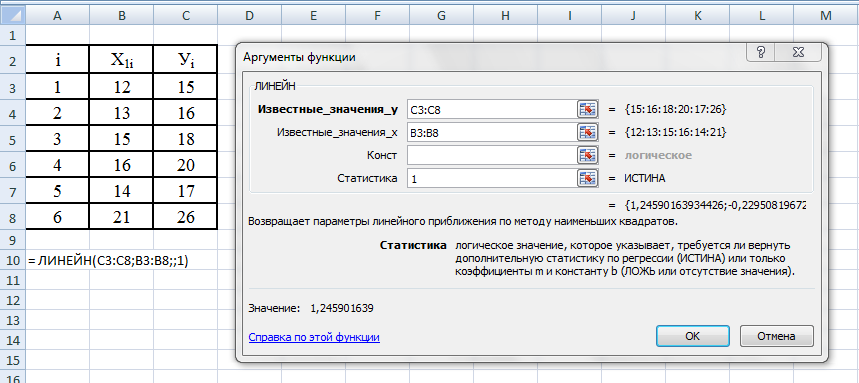
Шаг 4. Ок.
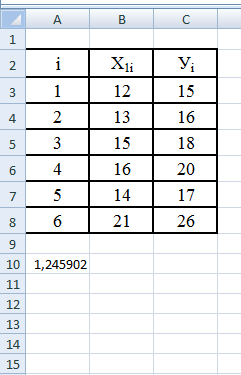
Шаг 5. Превращаем введенную функцию в матричную.
- выделяем диапазон ячеек А10:В14;
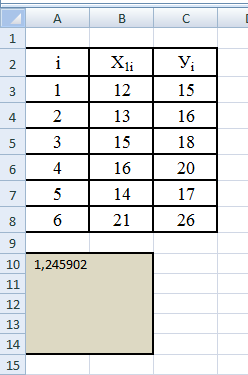
- нажимаем клавишу F2;
- последовательно нажимаем, не отпуская, три клавиши
Ctrl, Shift, Enter отпускаем клавиши.
Приводим характеристики эконометрической модели с использованием протокола расчетов по функции «Линейн».
У = -0,22951 + 1,245902*Х + е (линейная регрессионная модель)
0,707069 0,0445784 (ошибки коэффициентов модели)
R2 = 0,994827 (коэффициент детерминации)
Е = 0,326431 (ошибка модели)
F = 740,5128 (критерий Фишера)
(n-k) = 4 (число степеней свободы для остатков)
Cрег = 78,9071 (вариация для регрессии)
Сост = 0,42623 (вариация для остатков)
Приводим протоколы расчетов характеристик линейной модели с помощью программы Ехсе1 «Регрессия»
Шаг 1.
Копируем таблицу с данными и вставляем ее в лист Ехсе1.
Шаг 2. Обращаемся к программе «Регрессия»
Проходим путь к программе «Регрессия»: Данные, Анализ данных, Регрессия
Шаг 3, ОК, вводим минимальные параметры программы регрессия, чтобы не загромождать протокол расчетов,
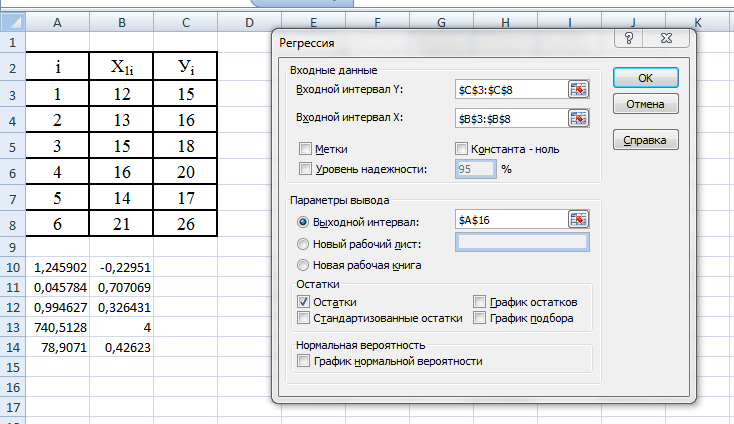
Шаг 4. ОК.
Все характеристики линейной модели, рассчитанные по функции Линейн совпадают с значениями, рассчитанными с помощью программы Регрессия. Однако, программа Регрессия позволяет вычислить гораздо больше характеристик модели, чем с помощью функции Линейн.
Протоколы расчетов, полученные с помощью программы Регрессия, обладают одним неприятным качеством – результаты расчетов автоматически не пересчитываются при изменении данных, а у функции Линейн протокол расчетов пересчитывается при изменении базы данных.
Однако, протоколы расчетов, выполненных с помощью Регрессия, очень удобно размещать в отчеты по эконометрическому анализу, а протоколы расчетов функции Линейн надо расшифровывать.
Выполним расчеты характеристик линейной модели с помощью программы Stadia 8.
Шаг 1. Обращаемся к программе Stadia 8, вводим данные Х и У.
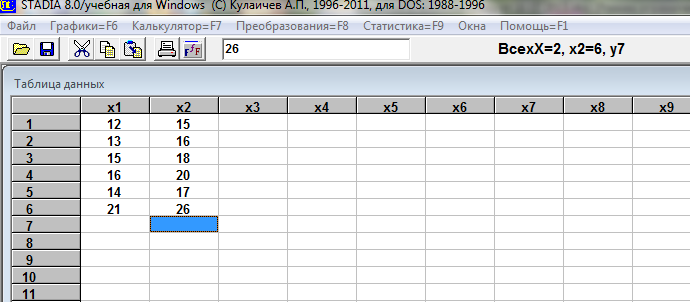
Шаг 2. Выбираем пункт меню «Статистика=F9»
Шаг 3. В разделе «Регрессионный анализ» выбираем «L=Простая регрессия/тренд», переносим Х1 в Х, Х2 переносим в У.
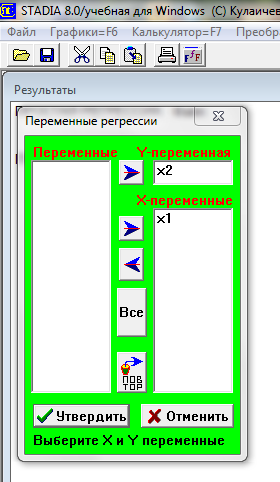
Шаг 4. Утвердить.
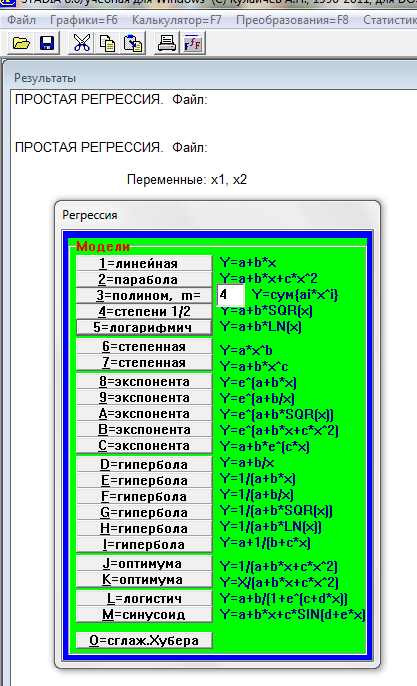
Нам предлагается выбрать одну из 22 математических моделей
Шаг 5. Выбираем «1=линейная»
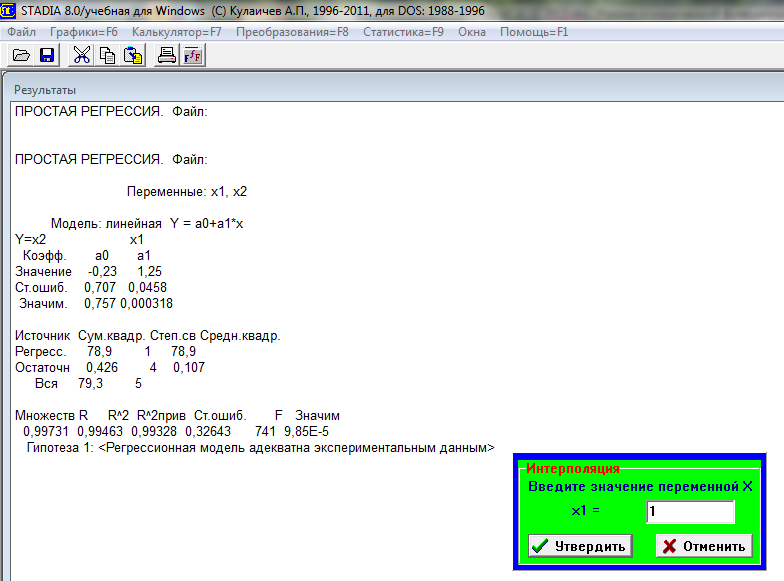
Мы получили основные характеристики линейной модели, которые полностью совпадают с расчетами по функции Линейн и программы Регрессия. Продолжаем проведение расчетов.
Шаг 6. Введем ожидаемое значение Х, равное, допустим 25, утвердить.
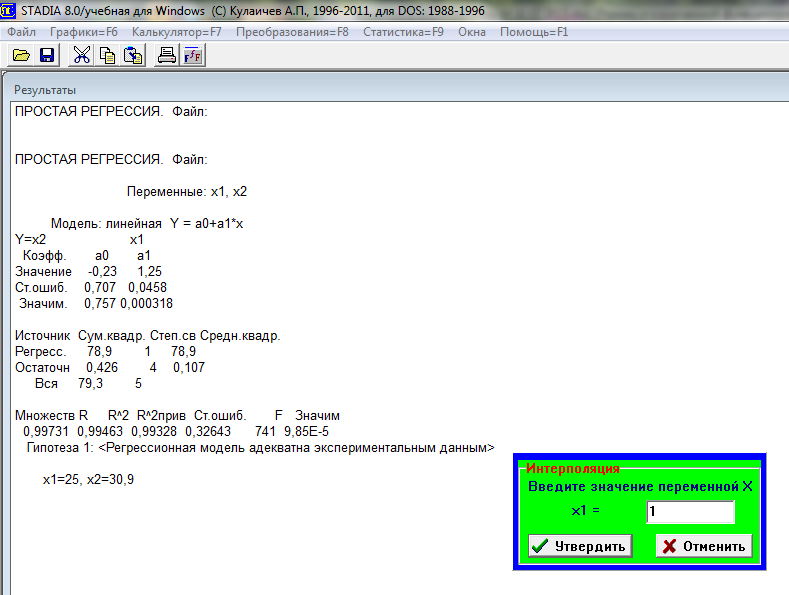
В расчетах появилось значение У = 30,9 при значении Х=25.
Шаг 7. Заканчиваем расчеты. Отменить.
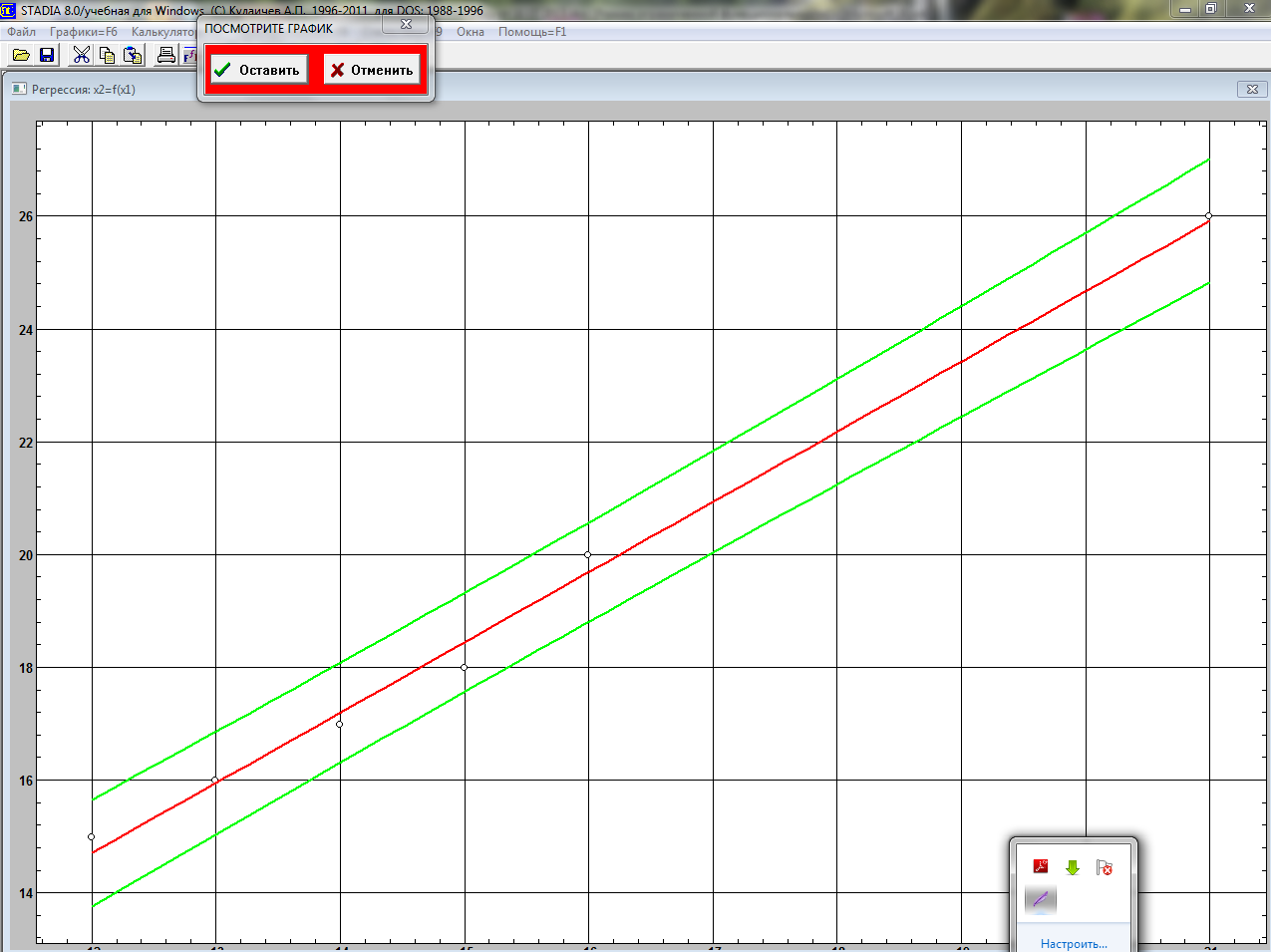
Появляется график зависимости У от Х, расчетные значения Ур и доверительные интервалы уравнения регрессии.
Шаг 8. Продолжаем заканчивать расчеты. Отменить
Нам предлагается провести анализ остатков, выполнить прогнозирование, выбрать новую модель или закончить анализ.
Выбираем закончить анализ. Вы, конечно, можете продолжать, но для первого знакомства с программой вполне достаточно.
В полученном протоколе расчетов обратите внимании, что в низу имеется три листа: Dat, Rez, Grl, означающие лист с данными, протокол расчетов, график.
Протокол расчетов можно сохранить с помощью меню программы
Шаг 9. Закрываем программу.
Файл, выход.
Повторим расчеты характеристик линейной модели с помощью сайта math.semestr.ru.
Шаг 1. Обращаемся к сайту «Онлайн-калькулятор» math.semestr.ru., эконометрика
Шаг 2. Выбираем в разделе Эконометрика «Уравнение парной линейной регрессии»
Нам предлагается посмотреть лекции, примеры решенных задач, ввести свои данные и получить готовые расчеты в текстовом виде.
Посмотрим лекции, затем введем свои данные и получим расчеты.
Шаг 3. В меню выделяем «Лекции»
Нам предлагается посмотреть на список использованной литературы при проведении расчетов и четыре темы лекций.
В списке литературы обратите внимание на то, что учебник и практикум Валентинова В.А. входит в десятку рекомендованных и это приятно.
При желании почитайте лекции по эконометрике по четырем темам.
Проведем расчеты характеристик линейной модели.
Вернемся на вкладку «Уравнение регрессии»
Шаг 3. Введем количество строк, равным 6, далее
Шаг 4. Введем численные значения Х и У, укажем основные характеристики, которые надо рассчитать, далее
Шаг 5. Выбираем вывод протокола расчетов.
Нам предлагают большой набор разнообразных расчетов, однако для первого знакомства ограничимся выбором «получить расширенное решение данной задачи»
Шаг 6. Выбор примера решения задачи.
Нам предлагают заплатить денежку. В прошлом году расчеты проводились бесплатно. Денежку платить не будем, а посмотрим готовые расчеты по другим данным.
Активизируем «Пример подробного нахождения параметров уравнения регрессии».
Шаг 7. Изучаем протокол расчетов.
Приводим фрагмент текста, который размещается на 12 листах с подробным описанием расчетов и формул. При желании посмотрите самостоятельно.
Шаг 8. Выходим из сайта.
Закрываем все вкладки и выходим из сайта.
Повторить расчеты нам не удалось, так как находимся в рыночной экономике и разработчикам сайта надо кормить семью. А работу они провели очень большую и с каждым годом добавляют количество моделей по многим экономико-математическим дисциплинам.