11. Построение линейной модели
Рассмотрим простейшую модель экономического процесса, состоящую из одного уравнения, которое содержит только две переменные.
Обозначив переменные буквами У и Х, мы постулируем между ними зависимость:
Уi=f(Хi)+ εi.= Урi + εi
Простейшим соотношением между двумя переменными является линейная связь между ними:
Урi=f(Хi) = α0+ α1Хi
Уi = α0+ α1Хi+εi, σε2 ,
где α0, α1 – неизвестные параметры,
ε – случайное возмущение, которое отражает влияние: тех факторов, которые не вошли в модель, ошибок наблюдений или измерений.
σε2 - дисперсия возмущения.
Параметры α0, α1 и дисперсия σε2 неизвестны.
Мы хотим на основании наших выборочных наблюдений над У и Х статистически оценить параметры α0, α1 с помощью следующей регрессионной модели:
Уi = Урi + ei = а0 + a1Хi+еi,
где а0, а1 - коэффициенты, которые являются оценками параметров α0, α1,
е – остатки модели, которые являются оценками возмущения ε.
Урi = а0 + a1Хi
Напомним основные понятия регрессионного анализа на примере решения задачи.
Имеются численные значения двух показателей: количество продавцов и розничного товарооборота по четырем выборочным однородным магазинам одной фирмы, представленные в таблице 6.
Таблица 6 - База данных по четырем филиалам одной фирмы
-
i
Хi
Уi
1
1
4
2
3
6
3
2
7
4
4
10
5
5
?
где i - номер магазина фирмы, индекс для переменных,
Х - количество продавцов (чел.),
У - величина розничного товарооборота (тыс. руб.).
Необходимо получить прогноз розничного товарооборота для открывающегося пятого магазина фирмы, в котором ожидается количество продавцов, равное пяти.
Полученный прогноз необходим для определения ориентировочной величины плана товарооборота для нового магазина фирмы.
Решение задачи
Приводим анализ задачи для формирования общекультурной компетенции: «культура анализа объекта изучения».
Анализ задачи можно проводить как по выделению элементов, так и по их анализу.
Анализ задачи по выделению элементов означает следующее:
- задача имеет номер, условие, таблицу данных, пояснение к таблице, что необходимо найти, для чего необходим прогноз;
- таблица данных имеет следующие элементы: название, три колонки и пять строчек, пояснение;
- колонки таблицы имеют соответствующие названия: i - номер магазина фирмы, Хi - количество продавцов (чел.), Уi - величина розничного товарооборота (тыс. руб.);
- все ячейки таблицы заполнены;
- в пятой строчке колонки Уi стоит вопрос.
Вывод: задача содержит все необходимые элементы.
Изучение задачи по анализу элементов показывает, что:
- в условии задачи указано, что анализируемые магазина являются однородными, это означает, что магазины не сильно отличаются по основным признакам: ассортимент, покупательная способность покупателей, машины и оборудование, торговые площади, место расположения, технология и форма обслуживания, оказываемые услуги покупателям, раскладка товара, квалификация продавцов, культура обслуживания, культура общения продавцов между собой, наличие документов на ведение торговли, комфортность торгового зала для покупателей и продавцов, наличие нормативных документов, регламентов и обеспечение безопасности торговли и товаров (следует отметить, что приведенные признаки магазина можно сгруппировать в шесть групп факторов);
- в первом магазине работает один продавец, который обеспечивает получение товарооборота в 4 тыс. руб.;
- во втором магазине работает 3 продавца, которые обеспечивают получение товарооборота в размере 6 тыс. руб.
Если второй магазин имел бы одинаковые значения факторов, обеспечивающие получение товарооборота, такие как: ассортимент, цена, наличие очереди, торговая площадь, место расположения относительно метро или потока жителей района, покупательной способности покупателей, культуры обслуживания, размещения товара на полках, то товарооборот должен бы составить 3*4 = 12 тыс. руб.
Фактически, товарооборот во втором магазине в два раза меньше своей потенциальной возможности 12/6 = 2 раза, так как помимо влияния числа продавцов на товарооборот оказывает влияние большое количество неучтенных факторов, которые снизили товарооборот во втором магазине.
Очевидно, что количество продавцов влияет на товарооборот, но при условии наличия очереди.
Если в магазине имеется очередь, то увеличение продавцов будет приводить к увеличению товарооборота, следовательно, товарооборот будет зависеть от количества продавцов.
Если в магазине нет очереди, то увеличение продавцов не приводит к увеличению товарооборота.
Вывод: товарооборот будет зависеть от количества продавцов при условии наличия в магазине очереди. Следовательно, на наличие связи между двумя переменными наложено одно условие.
Модель будет отражать выявленную закономерность, если выполняются определенные условия.
В третьем магазине работают 2 продавца, которые обеспечивают получение товарооборота 7 тыс. руб. Аналогичные рассуждения позволяют утверждать, что численные значения факторов, влияющих на товарооборот, не позволяют получить преимущества по сравнению с первым магазином, так как потенциальная возможность третьего магазина составляет 4*2 = 8 тыс. руб.
Общая тенденция зависимости У от Х является прямо пропорциональной.
Вывод: на зависимую переменную влияет большое количество факторов, которые все очень трудно учесть, поэтому выделяют только самые важные для исследования, влияние остальных факторов является случайной составляющей зависимой переменной.
Построение графика зависимости У от факторов Х является первым необходимым этапом любого эконометрического анализа (формирование общекультурной компетенции: культура мышления – представление данных в наглядном виде) см. рис. 6.
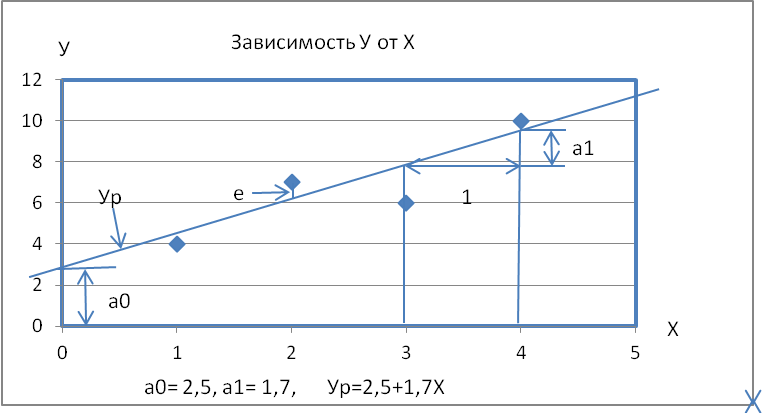
Рис. 6 - Графический анализ данных
Где на графике 6 а0 – свободный коэффициент, а1 – коэффициент влияния Х на У, е – остатки модели.
Проведем аппроксимационную линию так, чтобы разница между фактическими и расчетными значениями розничного товарооборота (остатки) были минимальными.
Если говорить более строго, то необходимо так провести линию, чтобы сумма квадратов остатков была минимальной.
Для оценки параметров , и возмущения , будем использовать коэффициенты а0, а1 и остатки е следующего линейного парного уравнения регрессии, вычисленных по выборочной совокупности объемом n = 5:
Уi= Урi+еi = а0+а1Хi+еi
где Уi - фактические значения розничного товарооборота;
i – порядковый номер измерения;
а0 – свободный коэффициент линейного уравнения регрессии равный значению Ур при Х = 0;
а1- коэффициент пропорциональности между У и Х, равный приросту Ур при изменении Х на единицу, или сколько товарооборота приходится на одного продавца, или на сколько увеличивает товарооборот один продавец, что означает среднею производительность труда продавцов;
Урi = а0 +а1*Хi - расчетные значения розничного товарооборота;
еi = Уi - Урi - остатки модели, учитывающие влияние факторов, не включенные в модель.
Визуальный анализ графика зависимости У от Х позволяет приблизительно вычислить коэффициенты однофакторной регрессии.
а0=2,5
а1 =1,7
Ур =2,5+1,7 * Х
Если в уравнение регрессии подставить ожидаемое значение Хож = 5, то можно получить прогнозное значение Упр.
Упр =2,5+1,7*Хож = 2,5+1,7*5 =11 тыс. руб.
Вывод.
Для выборочной совокупности фирм зависимость розничного товарооборота от количества продавцов можно представить в виде однофакторного линейного уравнения регрессии:
Уi =2,5+1,7 * Хi+ei.
Средняя производительность труда продавцов составляет 1,7 тыс. руб. на одного продавца.
Если в новой фирме ожидается 5 продавцов, то среднее прогнозное значение товарооборота будет равно 11 тыс. руб.
Однако, коэффициенты а0, а1, определенные по выборки равной пяти будут отличаться от истинных параметров , , которые можно определить по всей генеральной совокупности.