Этап 4. Обработка результатов эксперимента.

Опыт 1.

4.1. В соответствии с формулой (5) для цепей 1-го порядка (RC-цепи, LC-цепи) произведение . Рассчитайте это значение для экспериментально полученных значений и .

4.2. Рассчитайте значения абсолютных и относительных погрешностей измерения этих параметров.

4.3. Составьте программу и рассчитайте на ПЭВМ аппроксимирующую функцию , используя метод наименьших квадратов. Составьте программу и постройте график этой функции в формате А4. Нанесите на график экспериментально полученные точки и теоретическую зависимость (5).

Используя соотношения (9) и (10) рассчитайте границы допусков и нанесите их на экспериментальные точки.

Опыт 2.

4.4. Величина спада импульса на выходе схемы с «закрытым» входом определяется соотношением (7). Проверьте это соотношение, подставляя в формулу экспериментальные данные.

4.5. Используя результаты расчетов и эксперимента, определите реальную относительную погрешность измерения спада импульса:

4.6. Результаты расчетов занесите в таблицу 2.

Опыт 3.

4.7. Используя формулы (5) и (7) , рассчитайте граничные частоты исследуемой схемы. Сравните с измерениями классическим способом.

5. Выводы.

6. Контрольные вопросы

6.1 Дайте определение граничных частот АЧХ.

6.2 С чем связаны искажения прямоугольных импульсов в линиях передач?

6.3 Почему невозможно получить на практике прямоугольный импульс?

6.4 Поясните термин: «закрытый вход» измерительного устройства.

6.5 Почему появление фронта импульса называют искажениями в области «малых времен», а спад импульса—искажениями в области «больших времен»?

Аппроксимация экспериментальных данных методом нмк

Метод наименьших квадратов (НМК) — один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Метод наименьших квадратов применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина прямой или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятности; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Большие затруднения представляются при определении из наблюдений величин, которые не могут быть измерены непосредственно. Если, например, желают определить элементы орбиты планеты или кометы, то светила эти наблюдаются несколько раз, и в результате получают лишь координаты их (склонение и прямое восхождение) в известные времена; самые же элементы выводятся затем решением уравнений, связывающих наблюдаемые координаты с элементами орбиты планеты или кометы. При этом, если бы число уравнений равнялось числу неизвестных, то для каждой неизвестной получилась бы одна определенная величина; если же число уравнений больше числа неизвестных, то, вследствие ошибок наблюдений, результаты решений отдельных групп этих уравнений в различных сочетаниях оказываются не совсем согласными между собой.

До начала XIX в. учёные не имели опредёленных правил для решения системы уравнений, в которой число неизвестных менее числа уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Лежандру (1805—06) и Гауссу (1794—95) принадлежит первое применение к решению указанной системы уравнений теории вероятности, исходя из начал, аналогичных с началом арифметической середины, уже издавна и, так сказать, бессознательно применяемых к выводам результатов в простейшем случае многократных измерений.

Как и в случае арифметической середины, вновь изобретённый способ не даёт, конечно, истинных значений искомых, но даёт зато вероятнейшие значения.

Этот способ распространён и усовершенствован дальнейшими изысканиями Лапласа, Энке, Бесселя, Ганзена и др. и получил название метода наименьших квадратов, потому что после подстановки в начальные уравнения неизвестных величин, выведенных этим способом, в правых частях уравнений получаются если и не нули, то небольшие величины, сумма квадратов которых оказывается меньшей, чем сумма квадратов подобных же остатков, после подстановки каких бы то ни было других значений неизвестных. Помимо этого, решение уравнений по способу наименьших квадратов даёт возможность выводить вероятные ошибки неизвестных, т.е. даёт величины, по которым судят о степени точности выводов.

Рассмотрим в качестве примера аппроксимацию экспоненциальной функции методом НМК. Пусть аппроксимирующая формула имеет вид:

К такому виду функцию вида можно преобразовать следующей подстановкой:

Сделав подстановку , поучим требуемый вид функции.

Тогда сумма квадратов отклонений аппроксимирующей формулы от экспериментальных значений будет иметь следующий вид:

или

Поскольку нам необходимо найти коэффициенты a и b, обеспечивающие максимальную точность аппроксимации, найдем производные от суммы по этим коэффициентам:

Наилучшая точность аппроксимации соответствует минимуму функции , то поиск значений a и b сводится к решению системы уравнений

Подставив выражения, описывающие эти зависимости и преобразовав их, получим систему уравнений:

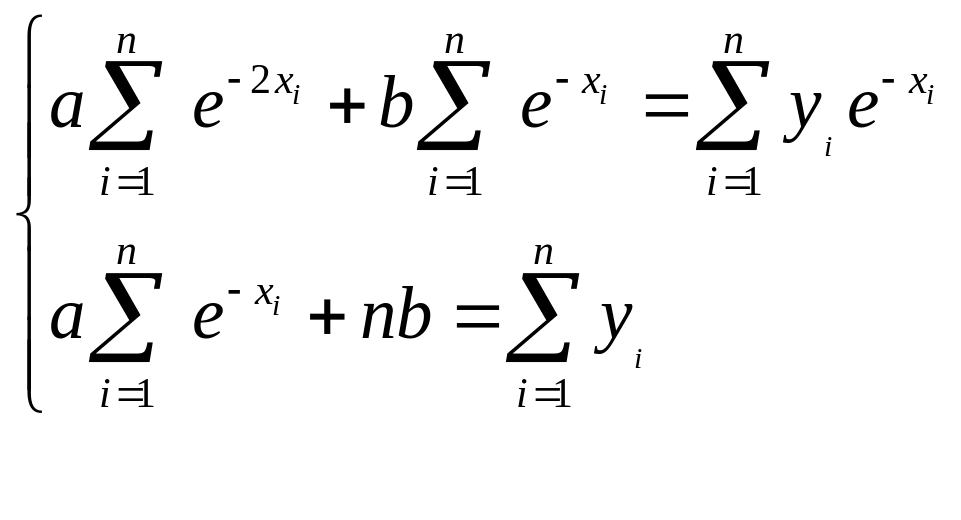
Решив эту систему, получим:

Для нахождения значений a и b по экспериментальным данным, удобно использовать программу Exel. Пример размещения данных на листе Exel показан на рисунке 7.

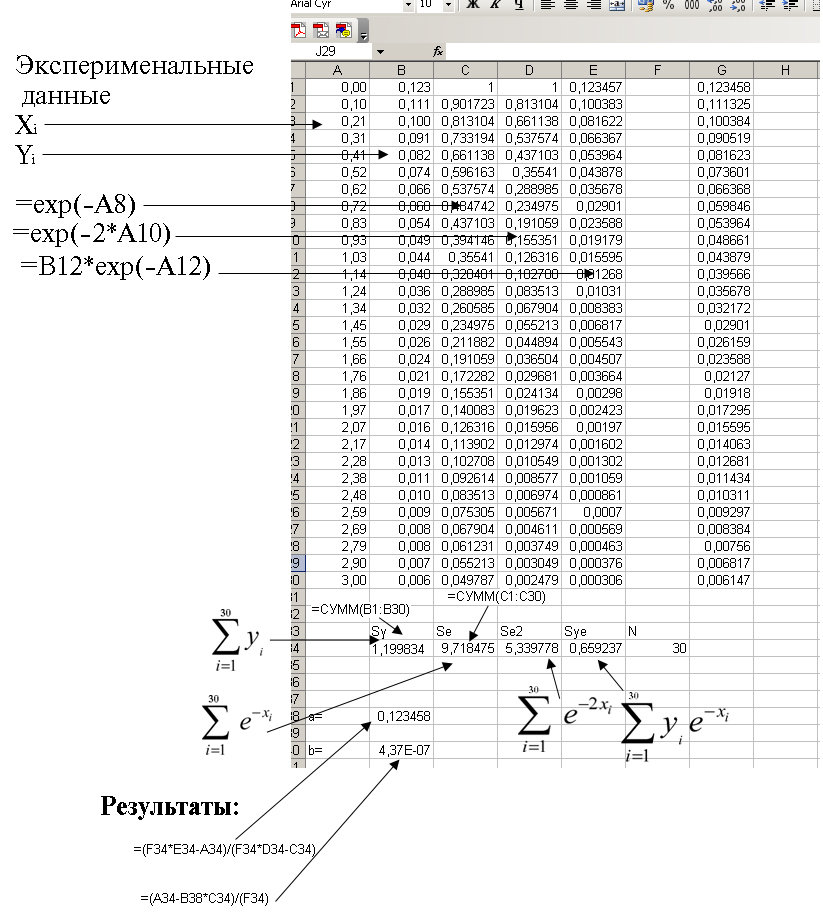
Рис. 7

В колонке А размещаются значения аргумента x_i, в колонке B – y_i, в колонке C – e^-Xi , в колонке D - e^-2Xi, в колонке E – y_ie^-Xi.

Внизу, под колонками, подсчитываются соответствующие суммы. И, в ячейках В38 и В40 – результат: значение коэффициентов аппроксимации.

Аналогичные формулы для гиперболической зависимости:

Для параболической зависимости нужно, рассчитав, как показано выше, соответствующие суммы, решить систему уравнений: