2.2 Физическая природа искажений прямоугольного импульса в линиях передач.

Любая линия передачи электрического сигнала ( свободное пространство, 2-х проводная линия, коаксиальный кабель, волновод, усилитель сигналов, измерительное устройство и др.) имеет ограниченную полосу пропускания—конечную верхнюю граничную частоту f . Модели сложных измерительных сигналов ( идеальные сигналы) --последовательность прямоугольных импульсов, «меандр», пилообразное напряжение и др. , имеют бесконечный спектр, т. е. для передачи такого сигнала без искажений требуются линии передачи с f = . Таких устройств не бывает. В реальных линиях передач с ограниченной полосой пропускания часть верхних составляющих спектра сигнала будет подавлена, что приведет к искажениям сигнала, называемым искажениями в области «малых времен».

Примечание:

Математически сигнал может быть представлен:

временной областью (аргумент-время t)

u(t)=U Sin(ώt+ )- синусоидальный сигнал,

u(t)= ( -пилообразный сигнал;

частотной областью (аргумент-частота f)

S( )=A A - амплитудный спектр сложного периодического сигнала,

здесь А -нулевая гармоника (постоянная составляющая сигнала),

А -амплитуда - гармоники сигнала.

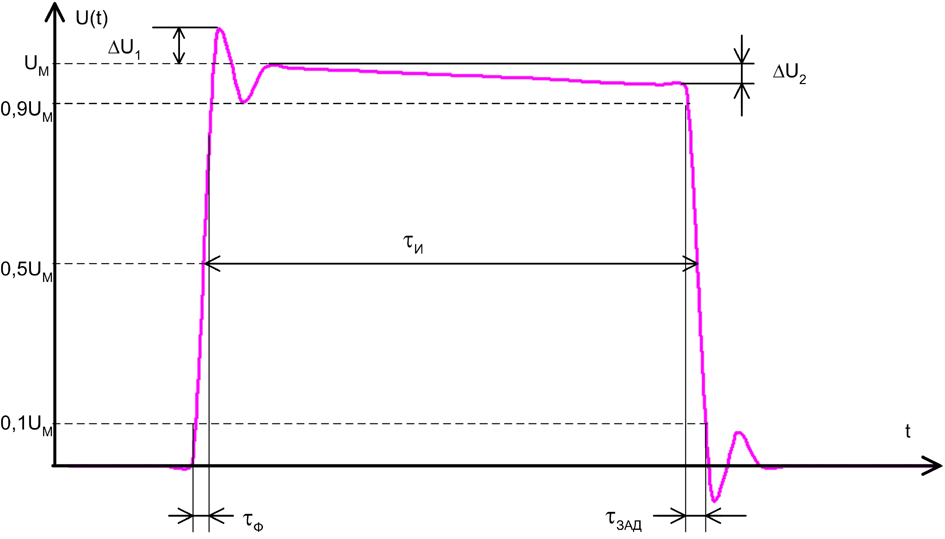
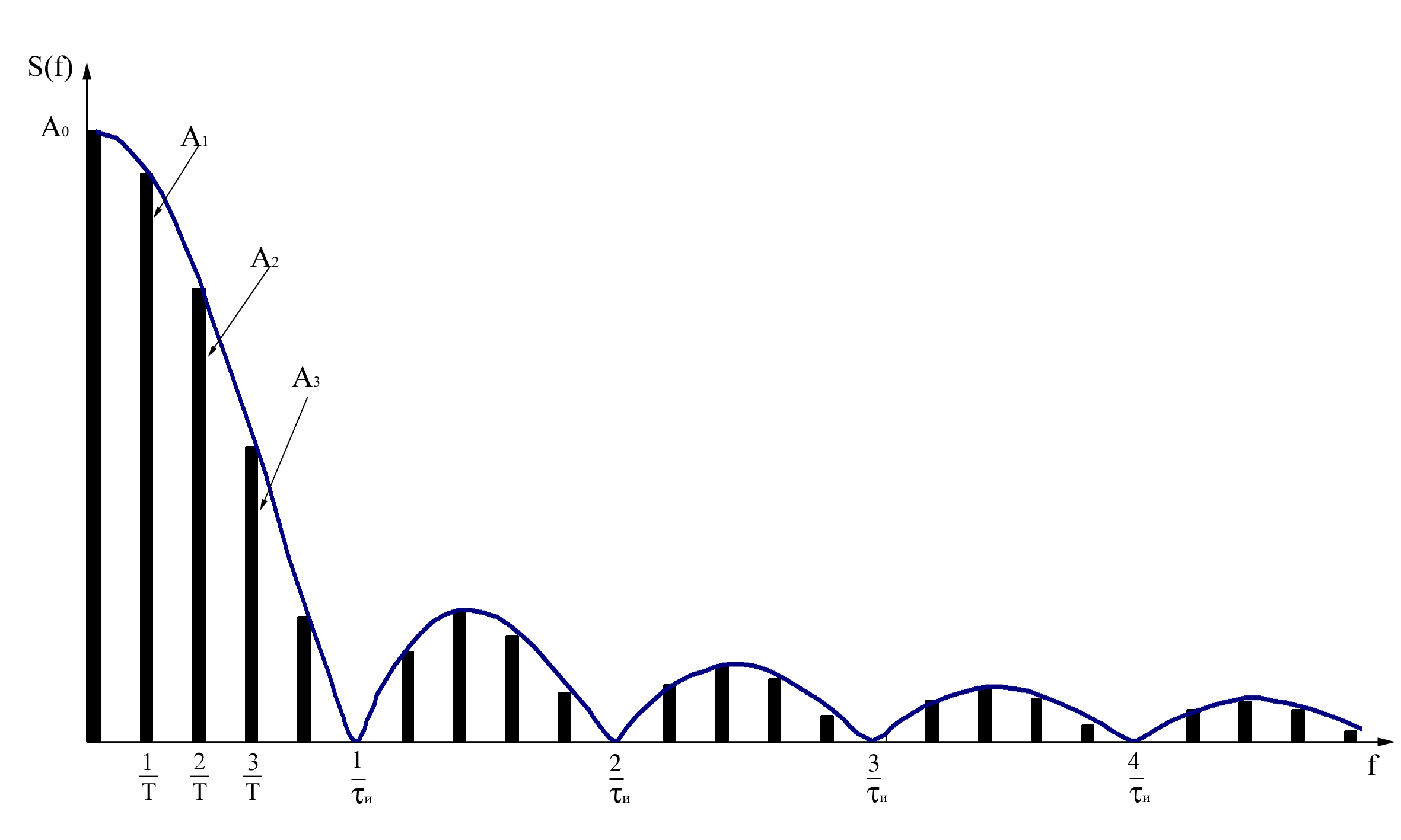
Рис. 1. Прямоугольный импульс с искажениями	Рис. 2. Амплитудный спектр последовательности прямоугольных импульсов

Поскольку период сигнала и его частота связаны обратным соотношением , то с увеличением частоты период (или время) уменьшается. Отсюда принято называть область больших (высоких) частот областью малых времен! А область низких частот - областью больших времен.

Если на входе электронного устройства или между каскадами усилителей ставится разделительный конденсатор, то такие линии передач не пропускают постоянную составляющую сигнала U , называются устройствами с «закрытым входом» и характеризуются параметром: нижняя граничная частота f_Н .

Верхняя и нижняя граничные частоты - это частоты, на которых коэффициент передачи сигнала уменьшается в раза (-3 дб.).

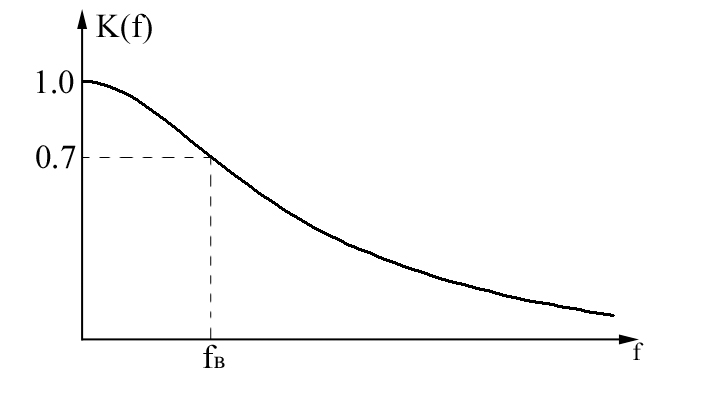
Линии передач с «открытым входом» характеризуются только верхней граничной частотой , а устройства с «закрытым входом»-нижней и верхней граничными частотами. На рис.3 представлен вид такой амплитудно-частотной характеристики (АЧХ).

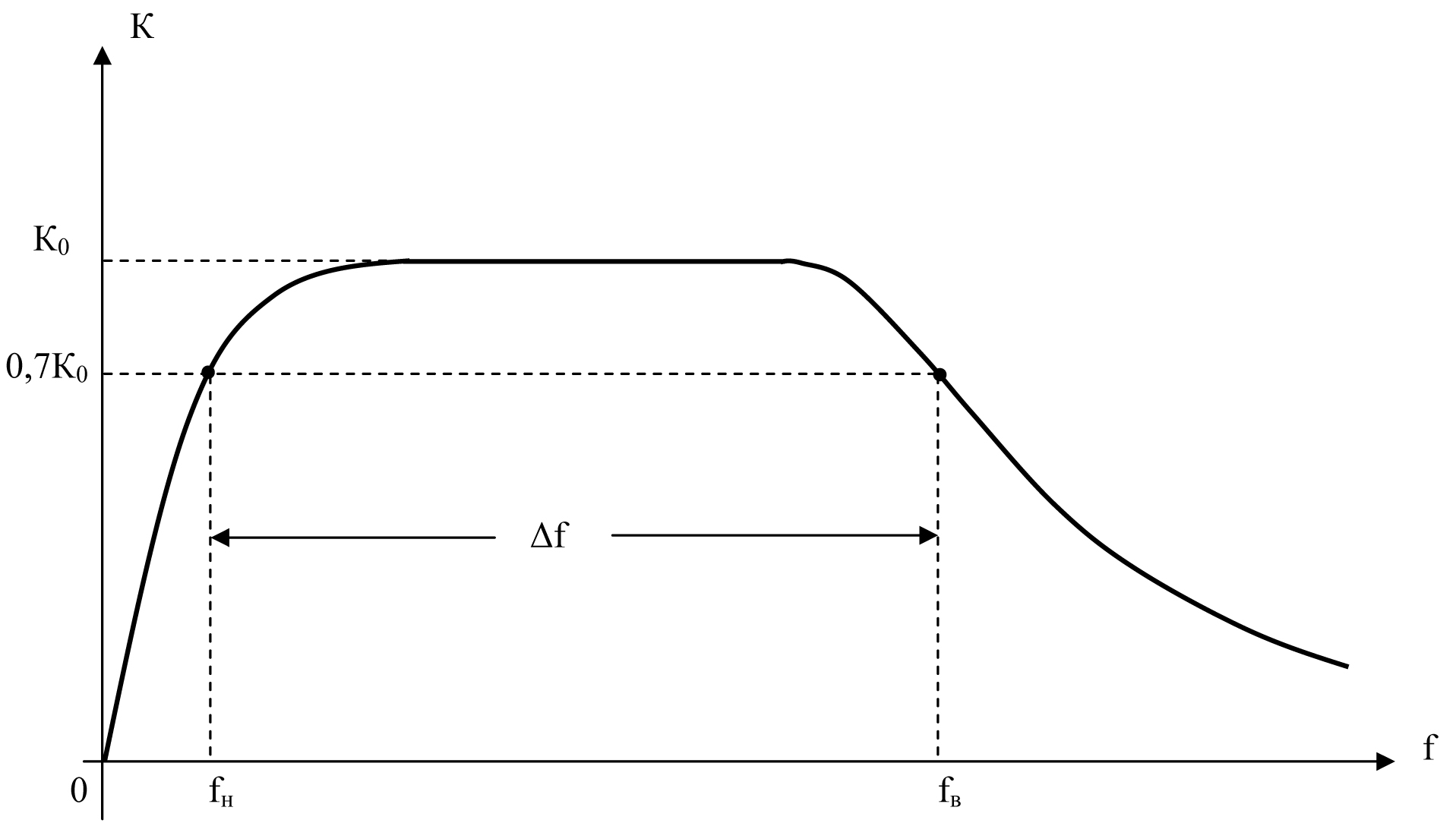
Рис.3. АЧХ линии передач с «закрытым входом».

Ограничение полосы пропускания линии передач сверху приводит к искажениям импульсного сигнала в области малых времен; эти искажения характеризуются длительностью переднего фронта импульса . Ограничение полосы пропускания снизу (f_Н ) приводит к искажениям импульса в области больших времен, которые характеризуются абсолютным ( ) или относительным ( ) спадом импульса (рис 1). Выброс характеризует переходные процессы (колебательный характер) в электронных схемах 2-го и более высоких порядков. В работе №5 исследуются искажения импульса в простейших RC- цепях (1-го порядка), поэтому выброс отсутствует (апериодический характер нарастания импульса).

2.3 Анализ ожидаемых искажений прямоугольного импульсного сигнала на выходе rc-цепи.

Искажения в области малых времен.

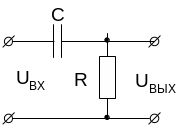
Примером простейшей линии передач с «открытым входом» является интегрирующая RC-цепь (рис.4а).

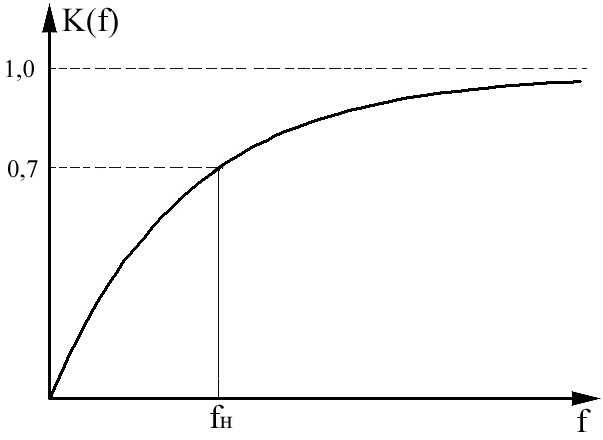
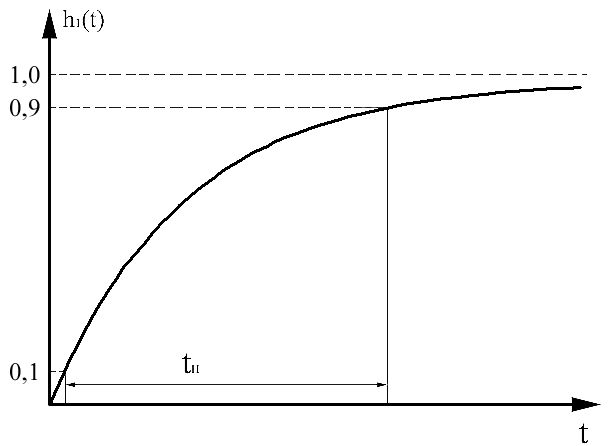
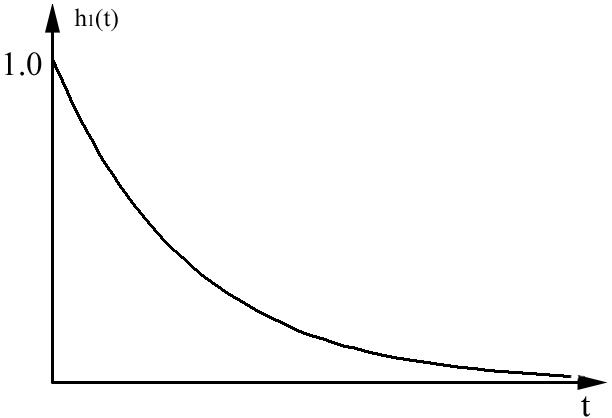
а) Интегрирующая RC-цепь	б) АЧХ интегрирующей RC-цепи	в) Переходная характеристика цепи (ПХ)
Рис.4.

Коэффициент передачи интегрирующей RC-цепи:

Зависимость модуля коэффициента передачи от частоты называется амплитудно-частотной характеристикой (АЧХ):

(1)

При

Частота

(2)

называется граничной (верхней) частотой интегрирующей цепи.

Переходная характеристика (отклик цепи при подаче на вход единичного скачка напряжения) имеет вид:

(3)

Параметром ПХ является время нарастания , которое определяется по ограниченную полосу пропускания, т. е. фактически являются «фильтрами нижних частот», для анализа искажений импульсного сигнала можно воспользоваться моделью ФНЧ на основе интегрирующей RC-цепи.

По формуле (5) можно оценить (приближенно) связь между значением верхней граничной частоты электронного устройства ( линии передач, измерительного устройства, усилителя сигналов и т. п.) и временем нарастания (фронтом импульса).

Эта формула позволяет экспериментатору определить время нарастания импульса (фронт импульса) в зависимости от параметров RC-цепи:

(4).

Подставляя выражение (2) в (4), получаем зависимость длительности фронта импульса от величины верхней граничной частоты:

(5)

Эта формула позволяет экспериментатору выбрать измерительный прибор, например осциллограф, с необходимой полосой пропускания, задаваясь допустимым искажением импульса (фронт импульса). И, наоборот, измеряя фронт импульса на выходе исследуемого электронного устройства, можно оценить его полосу пропускания (верхнюю граничную частоту).

Искажения в области больших времен.

В электронных схемах для развязки по постоянному току (чтобы не пропускать постоянную составляющую сигнала) ставят разделительный конденсатор C . Такие устройства, в том числе измерительные приборы, называют устройствами с закрытым входом.

Простейшей электрической цепочкой такого типа является дифференцирующая RC-цепь (рис. 5а).

а) Дифференцирующая RC-цепь	б) АЧХ дифференцирующей RC-цепи	в) Переходная характеристика цепи (ПХ)
Рис.5.

По аналогии с интегрирующей RC-цепочкой, нижняя граничная частота рассчитывается по формуле:

Искажения импульса в такой цепи оцениваются по переходной характеристике :

(6)

Здесь Т=RC --постоянная времени цепи.

Если амплитуду импульса взять равной , то подставляя в формулу (6) значения и , можно рассчитать спад (скол) импульса-искажения в области больших времен:

(7)

При малых значениях спада импульса это выражение можно упростить:

(8)

По этой формуле, зная нижнюю граничную частоту цепи и длительность импульса , можно определить спад (скол) импульса и наоборот.