
- •Введение
- •1 Общие вопросы расчета электрических сетей
- •1.1 Выбор напряжения
- •1.2 Выбор числа и мощности трансформаторов
- •1.3 Расчет параметров схемы замещения трансформаторов
- •1.3 Выбор компенсирующих устройств
- •Фактическая полная нагрузка подстанции после компенсации:
- •2 Расчет разомкнутой сети
- •2.1 Выбор схемы разомкнутой сети
- •2.2 Расчет мощностей и токов нагрузки разомкнутой сети
- •2.3 Расчет параметров схемы замещения разомкнутой сети
- •2.4 Расчет потерь напряжения, мощности и энергии разомкнутой сети
- •2.5 Проверка разомкнутой сети в послеаварийном режиме
- •3 Расчет замкнутой сети
- •3.1 Выбор схемы замкнутой сети
- •3.2 Расчет мощностей и токов нагрузки замкнутой сети
- •3.3 Расчет параметров схемы замещения замкнутой сети
- •3.4 Расчет потерь напряжения, мощности, энергии замкнутой сети
- •3.5 Проверка замкнутой сети в послеаварийном режиме
- •4 Технико-экономическое сравнение вариантов
- •4.1 Критерии сравнения вариантов
- •4.2 Составление сметы приведенных затрат
- •5 Выбор регулировочных ответвлений трансформаторов
- •5.1 Определение напряжений в узловых точках
- •5.2 Определение напряжения на стороне низшего напряжения подстанций
- •6 Расчет нормативных и удельных нагрузок на провод участка местной электрической сети
- •6.1 Выбор климатических условий
- •6.2 Удельные нормативные и расчетные нагрузки на провод
- •Литература
- •Приложение г (обязательное) Область применения и размеры унифицированных железобетонных и стальных промежуточных опор 35 кВ
- •Приложение д (обязательное) Исходные данные для расчета по вариантам
Фактическая полная нагрузка подстанции после компенсации:
Siф=![]() (18)
(18)
После выполнения расчетов по формулам (14),(14)',(15) полученные данные заносятся в таблицу 6.
Таблица 6 – Мощность компенсирующих устройств и потребителей
после компенсации
Подстанция |
Полная фактическая мощность, Siф, MBA |
Активная мощность, Р, МВт |
Реактивная Мощность Qi, MBAp |
Мощность К.У, Qку, МВАр |
Реактивная фактическая мощность, Qiф,МВАр |
а |
|
|
|
|
|
в |
|
|
|
|
|
с |
|
|
|
|
|
Примечание. В дальнейшем при расчетах и построении схем замещения указывается полная фактическая мощность Siф = pi + jqiф.
2 Расчет разомкнутой сети
2.1 Выбор схемы разомкнутой сети
Для выбора оптимальной схемы разомкнутой
сети необходимо выполнить перебор
всех возможных вариантов разомкнутой
сети и для каждого варианта определить
суммарную длину (т.е. сумму длин всех
участков). Вариант схемы, у которой
суммарная длина минимальная является
оптимальным. В системе координат х,
у наносятся координаты всех узловых
точек сети (это координаты всех
подстанций и источника питания).
Полученные точки соединяются линиями,
при этом, в первую очередь соединяют
источник "А" с той подстанцией,
на которой расположены потребители
категории. Это соединение выполняют
двойной линией (поясняя, что подстанцию
питают по двухцепной линии). Подстанции
с потребителями
![]() и
категорий соединяют последовательно
(т.е. без образования циклов) одной
линией (одноцепная линия) всеми
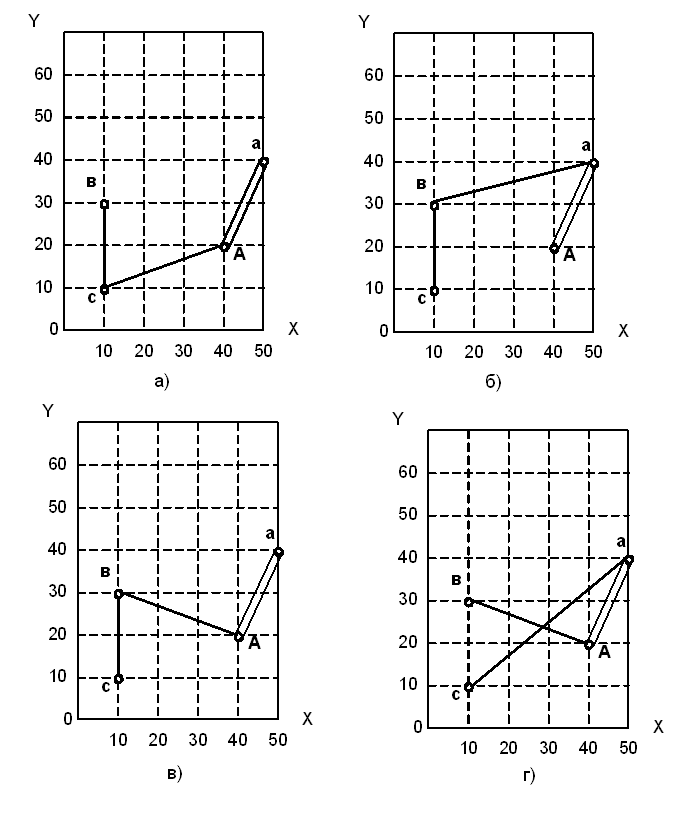
возможными способами. Геометрические
образы всех возможных схем разомкнутых
сетей изображены на рисунке 3.
и
категорий соединяют последовательно
(т.е. без образования циклов) одной
линией (одноцепная линия) всеми
возможными способами. Геометрические
образы всех возможных схем разомкнутых
сетей изображены на рисунке 3.
Число таких схем определяется по формуле
N = 2*V(V-3) , (19)
где V – число узлов разомкнутой сети (это число элементов множества А,а,в,с).
Длину отдельного участка сети определяют по формуле:
Lij
= m*![]() , (20)
, (20)
где m - масштаб, км/мм;
хi - абцисса i-го узла;
уi - ордината i-го узла;
хj - абцисса j-го узла;
уj - ордината j-го узла;
i - индекс, который принимает значения множества А,а,в,;
j - индекс, который принимает значения множества а,в,c;
причем i j .
Суммарная длина разомкнутой сети q-го варианта:
Lq
=
![]() , (21)
, (21)
где Lк - длина одного из участков разомкнутой сети, Lк = Lij q-го варианта (q = 1,2,3,..,N).
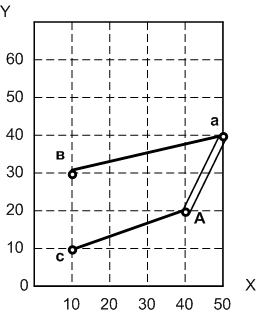
Выбрав схему оптимального варианта, необходимо начертить её в однолинейном исполнении (см. рисунок 4).
На выбранной схеме разомкнутой сети
указываются комплексы мощностей
подстанций
![]() = pi
+ qж,i
в узлах ("а","в","с"),
а над каждым участком наносится длина.
= pi
+ qж,i
в узлах ("а","в","с"),
а над каждым участком наносится длина.

Рисунок 4 - Однолинейная схема оптимального варианта

д) е)


ж) з)
Рисунок 3- Возможные схемы разомкнутых сетей
