1.3. Анализ поляризованного света

Анализ поляризованного света предполагает решение таких задач, как определение вида поляризации и оценка степени поляризации .

В основу анализа поляризованного света положен закон Малюса. Если на поляроид падает плоскополяризованный свет с амплитудой , составляющий угол с разрешенной плоскостью поляроида , то через него пройдет только «параллельная» компонента . Тогда в соответствии с рис. 7.8 получим:

, (7.5)

, (7.6)

. (7.7)

Выражение (7.7), устанавливающее соотношение между интенсивностью плоскополяризованного света до и после поляроида, является законом Малюса.

Если на пути исследуемого светового луча поместить поляроид–анализатор и вращать его вокруг оси, совпадающей с лучом, то возможны три варианта результатов:

1. Интенсивность проходящего света меняется по закону Малюса (7.7), это означает, что анализируемый свет плоско поляризован.

2. Интенсивность проходящего света после анализатора меняется по закону:

, (7.8)

это означает, что свет частично плоско поляризован, степень поляризации равна:

, (7.9)

Составляющая интенсивности в этом случае свидетельствует о наличии естественного или эллиптически поляризованного света.

3. Интенсивность проходящего света не изменяется. В этом случае свет или естественный или циркулярно-поляризованный.

В основу анализа эллиптически-поляризованного света положено действие фазовой пластинки. Поставленная на пути циркулярно-поляризованного света четвертьволновая пластинка преобразует его в плоскополяризованный. Поэтому, если исследуемый свет не является плоскополяризованным, то его можно анализировать при помощи ¼-волновой пластинки и поляроида – анализатора.

Если на пути луча поставить ¼-волновую пластинку, а затем поляроид и начать вращать его вокруг оси, совпадающей с лучом, то возможны следующие варианты результатов:

1. Интенсивность меняется по закону Малюса. В этом случае свет полностью циркулярно поляризован.

2. Интенсивность света не меняется. Это означает, что свет – естественный.

3. Интенсивность меняется по закону (7.7), в этом случае свет частично циркулярно поляризован. Степень его поляризации определяется по (7.9).

Перечисленные операции и полученные на их основе выводы исчерпывают все возможные случаи поляризации светового пучка.

Экспериментальная часть

Экспериментальная установка

Основой всех экспериментальных установок, используемых в работе, является оптическая скамья с набором рейтеров и осветитель с блоком питания. Включив источник света, проверьте его установку. При правильной установке лампы в осветителе на расстоянии м от него на экране должно получаться равномерно освещенное пятно диаметром см в дальнейшем сборку установок производить в соответствии со схемами, приводимыми в каждом задании.

Задание 1. Определение разрешенной плоскости колебаний поляроида

Это задание выполняется с помощью «черного» зеркала – гладкой полированной поверхности диэлектрика – стеклянной пластины, вставляемой в оправу, которая в свою очередь крепится на рейтере с круговой шкалой. Схема проведения наблюдений приведена на рис. 7.9.

Свет, отразившись под некоторым углом от черного зеркала З, должен попасть на поляроид П, вставленный в оправу с круговой шкалой, и далее в глаз наблюдателя. Наблюдая через поляроид П световой блик, отраженный от диэлектрика З и подбирая положение зеркала З – – вращением поляроида П вокруг луча на угол  добейтесь минимальной интенсивности пропущенного поляроидом света. В этом случае разрешенная плоскость поляроида горизонтальна. Отметьте ее положение мелом на оправе поляроида. Применяя общепринятые условия обозначения, покажите (в тетради) состояние поляризации луча в данной установке на виде сверху и сбоку.

Задание 2. Проверка закона Брюстера.

Соберите установку по схеме, изображенной на рис. 7.10.

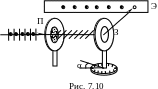
Разрешенная плоскость поляроида, устанавливаемого на оптической скамье, должна быть расположена горизонтально. Вращая «черное» зеркало вокруг вертикальной оси и наблюдая на экране за интенсивностью отраженного света (световое пятно на экране), найдите такое положение, когда пятно полностью гаснет. Этот угол ₀ и есть угол Брюстера для данного диэлектрика. По измеренному углу проверьте закон Брюстера, полагая, что показатель преломления стекла «черного» зеркала равен . Заполните таблицу 7.1.

Таблица 7.1.

; ; ;

Выставив теперь зеркало З под углом Брюстера и вращая поляроид П вокруг луча, можно добиться полного гашения пятна света на экране Э. В этом случае плоскость пропускания поляроида расположена горизонтально. Отметьте мелом положение метки на оправе поляроида, тем самым определите более точно положение разрешенной плоскости колебаний поляроида, чем в задании 1.

Повторите определение угла полной поляризации при отражении по схеме рис. 7.10 со вторым поляроидом из набора. Отметьте на его оправе разрешенную плоскость пропускания. Результаты внесите в таблицу.

Задание 3. Проверка закона Малюса

Соберите из осветителя, двух поляроидов и люксметра установку по схема рис. 7.11.

Вращая анализатор А вокруг луча, добейтесь максимального значения фототока. Меняя угол с шагом , получите зависимость фототока от угла . Результаты занесите в таблицу 7.2. Приняв максимальное значение фототока за , постройте график зависимости , прямолинейность этого графика подтверждает закон Малюса.

Таблица 7.2.

, град
, лк