Питання для самоперевірки

1. Запишіть основні види рівнянь прямої у просторі, поясніть зміст основних складових цих рівнянь:

• канонічне рівняння;

• параметричне рівняння;

• рівняння прямої, що проходить через дві точки.

2. Запишіть формулу для знаходження кута між двома прямими у просторі.

3. Сформулюйте умови паралельності і перпендикулярності прямих.

4. Розгляньте основні випадки розміщення прямої та площини в просторі.

5. Вкажіть умови паралельності і перпендикулярності прямої та площини у просторі.

Завдання

Складіть параметричне рівняння прямої, яка проходить через дві задані точки і .

Запишіть канонічне рівняння прямої, що проходить через точку паралельно прямій . Зведіть його до загального рівняння (у вигляді перетину двох площин).

Знайдіть гострий кут між прямими: і .

Обчисліть кут між прямою і площиною .

Для якого значення пряма паралельна площині ?

Знайдіть значення і , при яких площина перпендикулярна до прямої .

Рекомендована література

2. Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.:ЦУЛ, 2010. – С. 162-167.

3. Васильченко І.П. Вища математика для економістів: Підручник. – К.: Знання – Прес, 2002. – С. 120-128.

4. Математика для економістів: теорія та застосування./ Лавренчук В.П. та ін. - К.: Кондор, 2007. – С. 60-67.

5. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навч. посібник. – К.:ЦУЛ, 2005. – С. 118-121.

Теми 4-5. Вступ до математичного аналізу: функція, границя і неперервність функції

Питання для самостійної підготовки

Поняття функції, область визначення, способи задання.

Основні елементарні функції, їх властивості і графіки.

Перетворення графіків функцій.

Застосування функцій в економіці.

Неперервність функції в точці та на відрізку.

Точки розриву функцій, їх класифікація.

Основні теореми про неперервні функції.

Поняття, терміни та формули, які необхідно знати

Функція, способи задання функції.

Область визначення та область значень функції.

Способи перетворення графіків функцій.

Границя функції.

Теореми про границі (без доведення).

Методи знаходження границі функції в точці та на нескінченності.

Неперервність функції, поняття точки розриву.

Поняття функції, область визначення, способи задання

Розглянемо дві змінні величини х  D  R i y  E  R. Функцією y = f(x) називається така відповідність між множинами D i E, при якій кожному значенню змінної х відповідає єдине значення змінної у. При цьому вважають, що: х – незалежна змінна, або аргумент; у – залежна змінна, або функція; f – символ закону відповідності; D – область визначення функції; Е – множина значень функції. Розрізняють такі способи задання функції: аналітичний, графічний, табличний.
Функція у = F(u), де u = (x), називається складною (складеною) функцією, або суперпозицією функцій F(u) та (х), і позначається y = F( (x)).	– cкладена функція, у даному випадку вона є суперпозицією трьох функцій: у = 5u, u = v2 та v = sin x.
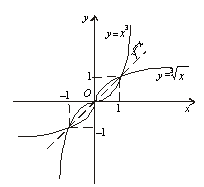
Нехай функція у = f(x) встановлює відпо-відність між множинами D та Е. Якщо обернена відповідність між множи-нами Е та D буде функцією, то вона називається оберненою до даної у = f(x); її позначають у = f –1 (x). За означенням, для взаємно обернених функцій виконується рівність: Графіки взаємно обернених функцій симетричні відносно прямої у = x.	та – взаємно обернені функції: .
Функція (функціональна залежність змінної у від змінної х) називається неявною, якщо її задано рівнянням F(x, y) = 0, яке не розв’язане відносно змінної у.	Рівняння задає неявну функцію у від х.
Система рівнянь визначає параметричну залежність функції у від змінної х (змінна t тут виступає параметром). Виразити залежність у від х у вигляді можна виключенням параметра t із даної системи рівнянь.	Параметрична залежність визначає коло радіуса R з центром у початку координат. Виконавши піднесення обох частин параметричних рівнянь до квадрату і підсумовуючи результат, дістанемо: , або .