Питання для самоперевірки

• Дайте означення вектора, сформулюйте правило виконання додавання векторів, множення вектора на скаляр (аналітично і графічно). Запишіть основні властивості дій над векторами.

• Сформулюйте означення базису на площині в просторі. Проілюструйте графічно розклад вектора за базисом.

• Виконайте побудову прямокутної декартової системи координат у просторі, вкажіть за малюнком:

• координатні осі та відповідні орти;

• координатні площини;

• радіус-вектор довільної точки М;

• координати точки М у просторі.

• Запишіть формули для знаходження у просторі:

1. координат вектора;

2. відстані між точками;

3. координат точки, що поділяє відрізок у заданому відношенні.

• Запишіть формули для знаходження напрямних косинусів даного вектора простору. Яка умова виконується для напрямних косинусів?

• Дайте означення, вкажіть формулу для обчислення і особливості застосування скалярного, векторного та змішаного добутків.

Завдання

1. Переконайтесь, що система векторів { } утворює базис у просторі; знайдіть координати вектора у цьому базисі:

.

2. Знайдіть кут між векторами і , якщо

.

3. Перевірте, чи колінеарні вектори , побудовані на векторах :

.

4. Виконайте перевірку на компланарність векторів :

.

Рекомендована література

1. Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.:ЦУЛ, 2010. – С. 125-139.

2. Васильченко І.П. Вища математика для економістів: Підручник. – К.: Знання – Прес, 2002. – С. 82-114.

3. Математика для економістів: теорія та застосування./ Лавренчук В.П. та ін. - К.: Кондор, 2007. – С. 48-54.

4. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навч. посібник. – К.:ЦУЛ, 2005. – С. 48-54.

5. Богомолов М.В. Практичні заняття з математики, 1990. – С. 269-281, 335-343.

6. Богомолов Н.В., Сергиенко Л.Ю. Сборник дидактических заданий по математике. – М.: Высш.шк., 1987. – С. 29-32, 43-47.

Тема 3. Аналітична геометрія: Пряма і площина в просторі

Питання для самостійної підготовки

1. Пряма в просторі.

2. Співвідношення між прямими і площинами.

Поняття, терміни та формули, які необхідно знати

Канонічне та параметричне рівняння прямої у просторі.

Рівняння прямої, що проходить через дві точки.

Кут між двома прямими у просторі.

Умова паралельності і перпендикулярності прямих.

Взаємне розміщення прямої і площини у просторі.

Пряма в просторі

Пряма у просторі може бути визначена як перетин двох площин:

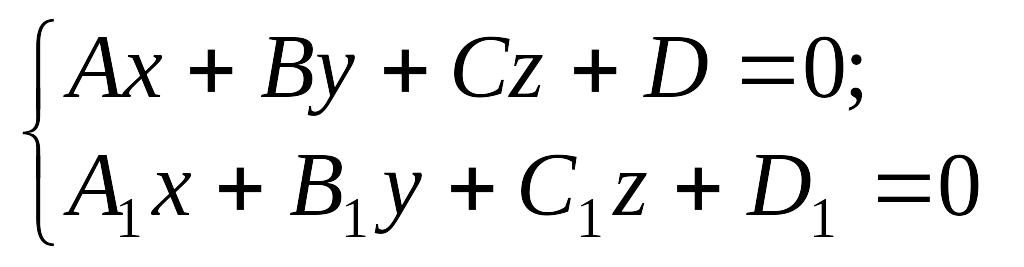
або канонічним рівнянням:

,

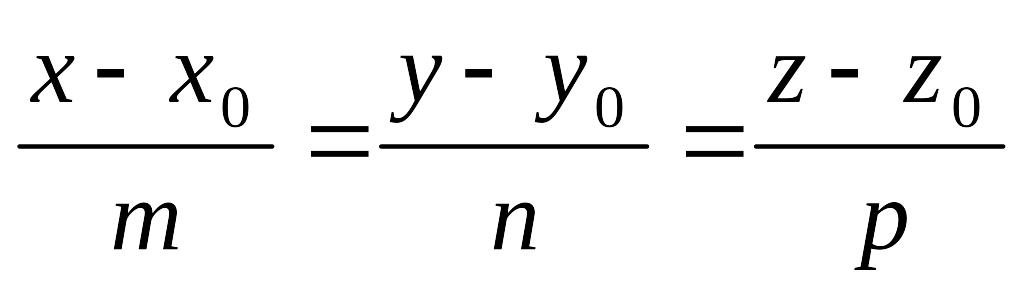де — напрямний вектор прямої, — точка, що лежить на прямій.

Пряму у просторі можна задати також параметричним рівнянням:

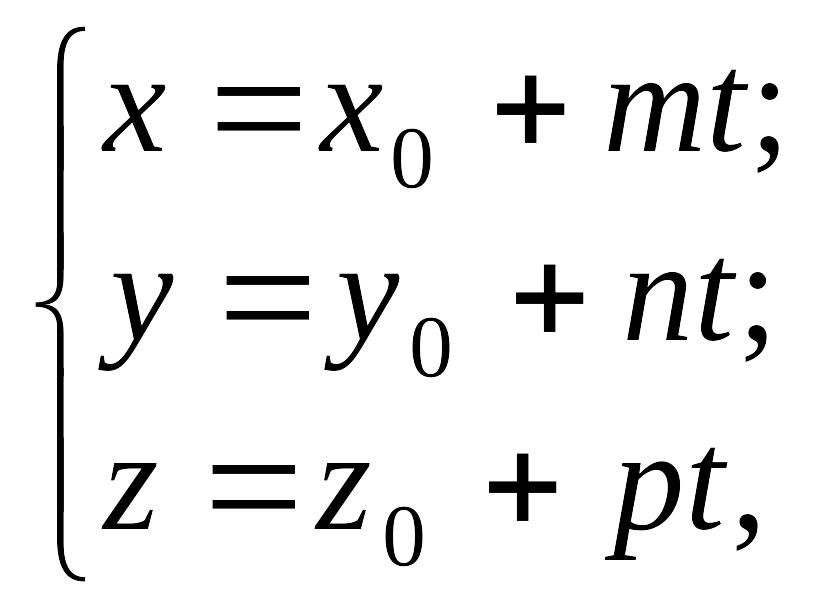
де t — параметр, або рівнянням прямої, що проходить через дві задані точки і :

.

Звичайно, всі рівняння відповідають прямій у просторі і між ними існує певний зв’язок.

Співвідношення між прямими і площинами

Площина і пряма у просторі можуть перетинатися під деяким кутом , який визначається за формулою:

.

У разі виконання умови: пряма і площина па- ралельні, а якщо — перпендикулярні. Умовою того, що пряма лежить на площині, є виконання співвідношень:

Приклад 1. Знайти напрямний вектор прямої

і кути, які вона утворює з осями системи координат.

Розв’язання. Вектори і перпендикулярні до відповідних площин, що задають рівняння прямої, тому напрямний вектор прямої розташований перпендикулярно до кожного з векторів . Згідно з означенням векторного добутку векторів

Тобто: або . Кути з осями знайдемо за формулами: ; .

Приклад 2. Показати, що прямі і перетинаються, і написати рівняння площини, в якій вони роз- ташовані.

Розв’язання. Дві прямі будуть лежати на одній площині, коли їх напрямні вектори і і вектор будуть компланарними.

Точка лежить на першій прямій, а — на другій.

Век­тор . Напрямний вектор . . 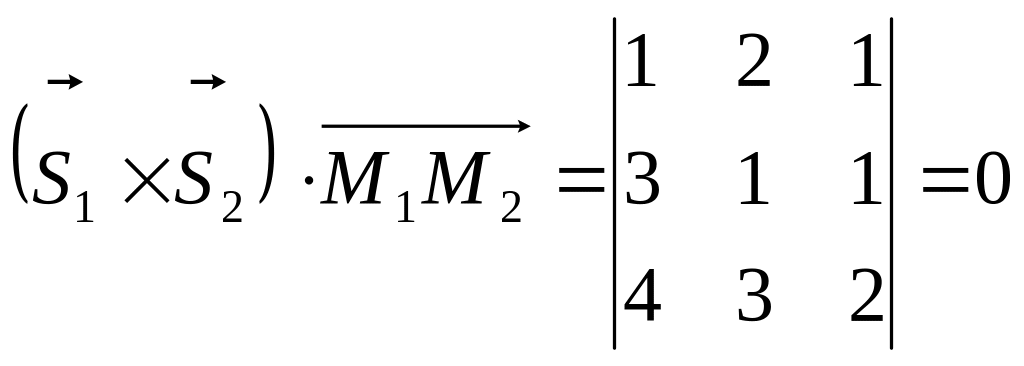Отже, прямі лежать на одній площині. Для запису рівняння цієї площини знайдемо вектор . Точка лежить на цій площині. Отже, маємо: або остаточно: .