Векторний добуток векторів

Векторним добутком неколінеарних векторів і називається вектор , напрямлений перпендикулярно до площини, в якій лежать ці вектори, у той бік, звідки найкоротше переміщення від першого вектора до другого видно проти годинникової стрілки. Модуль векторного добутку двох векторів дорівнює площі паралелограма, побудованого на цих векторах.

Векторний добуток позначається , або .

З означення випливає, що (4), де - кут між векторами і .

Якщо вектори і колінеарні, то кут між ними дорівнює або . Так як , то за формулою (4) маємо: .

Властивості векторного добутку

1. Для довільних векторів і при перестановці множників векторний добуток змінює знак, тобто (рис. 1).

2. Для довільного числового множника має місце сполучний закон, тобто .

3. Для довільних векторів , , має місце розподільний закон, тобто .

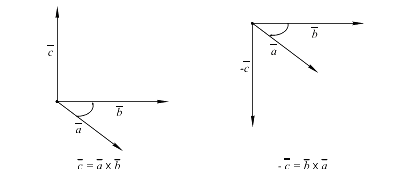
Рис. 1

Знаходження векторного добутку в координатній формі.

Нехай маємо два вектори тривимірного простору. Якщо , , то має місце формула:

(5)

Приклад. Знайти векторний добуток векторів і .

Використавши формулу (5), матимемо:

.

Таким чином, векторний добуток даних векторів .

Застосування векторного добутку

Векторний добуток застосовується для знаходження площі трикутника, побудованого на векторах і . Доповнивши трикутник до паралелограма, площа якого за формулою (4) дорівнює модулю векторного добутку даних векторів, матимемо формулу для обчислення площі трикутника:

(6)

Приклад. Обчислити площу трикутника, побудованого на векторах і .

Розв’язання. Скористаємось формулою (6) для знаходження площі трикутника. Обчислимо спочатку векторний добуток даних векторів.

.

Отже, векторний добуток даних векторів . Його модуль , а тому шукана площа трикутника (кв. од.).

Мішаний добуток векторів

Мішаним добутком упорядкованої трійки векторів , і називається число, рівне скалярному добутку вектора і вектора . Позначається змішаний добуток так: .

Геометричний зміст мішаного добутку: якщо вектори , і не лежать в одній площині, то модуль їх мішаного добутку дорівнює об’єму паралелепіпеда, побудованого на цих векторах.

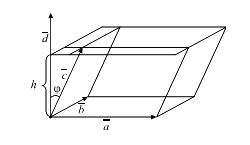
Рис. 2

Дійсно, як показано на рис. 2, (знак мішаного добутку залежить від кута ). Тому при використанні мішаного добутку для обчислення об’ємів паралелепіпеда та трикутної піраміди, побудованих на векторах , і , слід користуватись формулами:

(7)

(8)

Знаходження мішаного добутку в координатній формі

Нехай маємо три вектори тривимірного простору. Якщо , , то має місце формула:

(9)

Властивості мішаного добутку

1. Мішаний добуток підлягає сполучному закону, тобто для довільних векторів , і виконується: .

2. При циклічній перестановці векторів-множників мішаний добуток не змінюється, а при будь-якій іншій змінює знак на протилежний, тобто для довільних векторів , і виконується:

.

Приклад. Обчислити об’єм паралелепіпеда і піраміди, побудованих на трьох векторах: ; ; .

Розв’язання. Знайдемо спочатку мішаний добуток даних векторів за формулою (9):

.

Використавши формули (7) і (8) одержимо, що об’єм паралелепіпеда (куб. од.), а об’єм піраміди (куб. од.).