Прямокутна декартова система координат

Векторні простори , , можна розглядати відповідно як множину векторів на прямій (множину дійсних чисел), множину векторів на площині та множину векторів у тривимірному просторі. На відміну від векторів, числа називають скалярами.

На прямій , площині та у тривимірному просторі вектори можна геометрично зображати напрямленими відрізками. При цьому вони мають початок і кінець.

Систему векторів: та можна розглянути як базис простору , аналогічно вектори ; ; утворюють базис простору .

Числовою віссю називають пряму, на якій визначено:

1. напрям (®);

2. початок відліку (точка 0);

3. відрізок, який приймають за одиницю масштабу.

Дві взаємно перпендикулярні числові осі із загальним початком відліку (точка 0) називають прямокутною декартовою системою координат на площині (у двомірному просторі ).

Три взаємно перпендикулярні числові осі із загальним початком відліку (точка 0) називають прямокутною декартовою системою координат у просторі ( у тривимірному просторі ).

На рис. 1 зображені:

а) прямокутна декартова система координат на площині;

б) прямокутна декартова система координат у просторі.

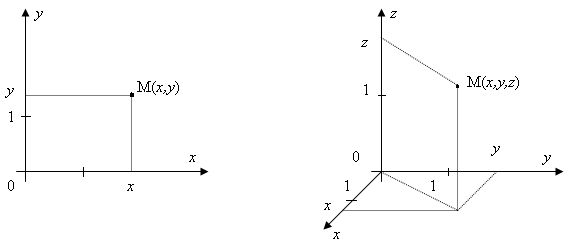
a) б)

Рис. 1

Вісь Ох називають віссю абсцис; Оу – вісь ординат; Оz – вісь аплікат. Орт осі Ох позначають , орт осі Оу – вектор , орт осі Оz – вектор .

Проекція вектора на вісь координати вектора на площині та в просторі

Упорядкована пара чисел (х,у), що відповідає точці М площини хOу, називається декартовими прямокутними координатами точки М на площині, це позначають М(х,у).

Упорядкована трійка чисел (х,у,z), що відповідає точці М простору 0zух, називається координатами точки М у просторі, це позначають М(х,у,z).

Відмітимо, що існують інші системи координат на площині та у просторі.

Введемо поняття проекції вектора на вісь. Нехай заданий вектор та вісь l. З точок А і В опускаємо перпендикуляри на вісь l. Одержимо точки А₁ та В₁ – проекції точок А та В.

Проекцією вектора на вісь називається довжина вектора , яка взята із знаком “+”, якщо напрям співпадає з напрямом осі та із знаком “-“, якщо напрями протилежні (рис. 2).

Позначається проекція вектора на вісь таким чином: пр₁ .

Кутом між двома векторами (або між вектором та віссю) називають найменший кут між їх напрямами при умові, що вектори зведені до спільного початку (рис. 2).

а) б)

Рис 2.

Знайдемо пр₁ :

У випадку а) маємо: пр₁ =

У випадку б) маємо:

пр₁ =

Таким чином, проекція вектора на вісь дорівнює добутку довжини вектора на косинус кута між вектором і віссю.

Координатами вектора називаються проекції вектора на осі координат.

Нехай вектор має координати а_х, а_у, а_z тобто = (а_х, а_у, а_z) і утворює з осями координат кути тоді

а_х = | | , а_y = | | , а_z = | | .

Косинуси кутів називаються напрямними косинусами вектора . З попередніх формул маємо:

.

Розглянемо вектор , де М₁(х₁,y₁) – початок вектора, М₂(х₂,y₂) – кінець вектора (рис. 3). У цьому випадку

тобто координати вектора - це впорядкована пара чисел (х₂ – х₁; y₂ – y₁).

Аналогічно одержуємо, що координатами вектора у просторі буде впорядкована трійка чисел (х₂ – х₁; y₂ – y₁; z₂ – z₁).

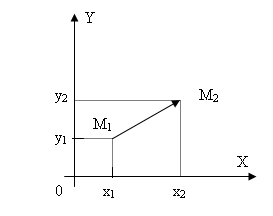
Рис. 3

Отже, можна сформулювати правило:

Координати вектора дорівнюють різниці відповідних координат кінця та початку вектора.

Наприклад, вектор , початок якого знаходиться в точці М₁(2,-3,0), кінець – в точці М₂(1,1,2), має координати:

= (1-2; 1+3; 2-0) = (-1; 4; 2)

Вектор (де точка О – початок координат) називають радіусом-вектором точки А і позначають . Координати вектора співпадають з координатами точки А.

Зауваження. По аналогії з векторами та вектор-рядок та вектор-стовпець, які містять n елементів, розглядають як вектори із n-вимірного простору Еⁿ, а їх елементи називають координатами вектора.

Наприклад, .

СКАЛЯРНИЙ, ВЕКТОРНИЙ І МІШАНИЙ ДОБУТКИ ВЕКТОРІВ,

ЇХ ГЕОМЕТРИЧНИЙ ЗМІСТ, ВЛАСТИВОСТІ ТА ЗАСТОСУВАННЯ

Скалярний добуток векторів

Скалярним добутком векторів та називають число, яке дорівнює добутку модулів цих векторів на косинус кута j між ними. Скалярний добуток векторів та позначають × , або ( , ).

Отже, згідно з означенням:

× = (1)

Знаходження скалярного добутку векторів та ,

заданих у координатній формі

Згідно з правилом множення матриць одержимо:

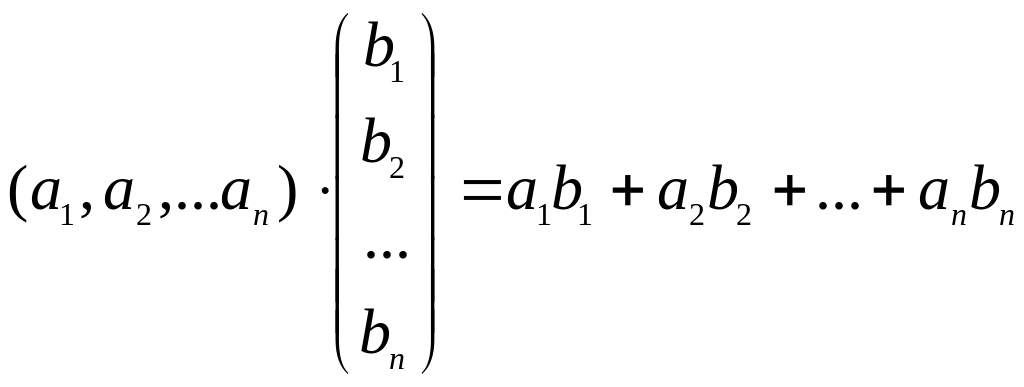× = (2)

тобто скалярний добуток двох векторів дорівнює сумі добутків їх однойменних координат.

Якщо = , тоді кут між цими векторами дорівнює нулю. Так як , то з формули (1) випливає, що .

Звідси одержуємо , або враховуючи формулу (2)

(3)

Властивості скалярного добутку

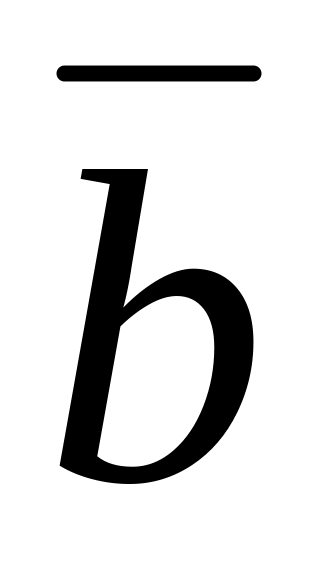1. Скалярний добуток підлягає переставному закону, тобто для довільних векторів і виконується : .

2. Скалярний добуток підлягає розподільному закону, тобто для довільних векторів , і 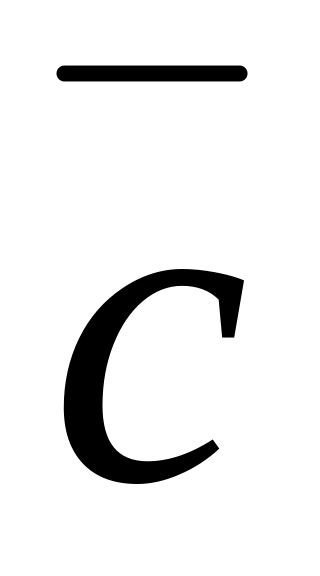виконується: .

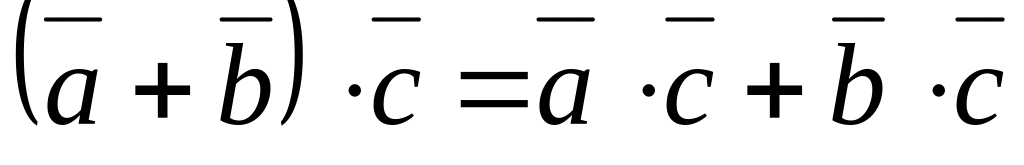3. Скалярний добуток підлягає сполучному закону відносно числового множника, тобто для довільних векторів , і числа 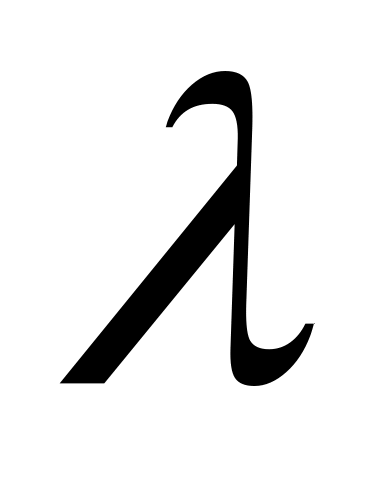виконується: .

Приклад 1. Знайти скалярний добуток векторів і .

Скориставшись формулою (2), матимемо:

.

Приклад 2. Знайти модуль вектора .

За формулою (3) одержимо:

.