Тема 2. Елементи векторної алгебри
Питання для самостійної підготовки
Основні поняття. Лінійні операції над векторами.
Лінійно залежні і незалежні системи векторів.
Базис, розкладання вектора за базисом.
Проекція вектора на вісь.
Прямокутна декартова система координат у просторі.
Скалярний, векторний, мішаний добутки, їх геометричний зміст, властивості та застосування.
Поняття, терміни та формули, які необхідно знати
Поняття вектора, дії над векторами.
Векторні простори.
Проекція вектора на вісь.
Базис на площині і в просторі.
Поділ відрізка в даному відношенні.
Розкладання вектора за базисом.
Скалярний, векторний і мішаний добутки векторів.
Кут між векторами.
Напрямні косинуси.
Умови колінеарності і компланарності векторів.
Основні поняття, лінійні операції над векторами
Вектором називають величину, яка характеризується не тільки своїм числовим значенням (довжиною), але й напрямком.
Вектори
позначають
або
.
При
позначенні вектора двома літерами
(наприклад,
)
перша літера вказує точку початку
вектора, а друга – точку його кінця.
В економіці вектори часто позначають однією великою літерою.
Довжину
(модуль) вектора позначають так:
,
.
Геометрично вектор зображують як напрямлений відрізок (рис.1)
Рис.1
Нульовим вектором називають вектор, початок і кінець якого співпадають.
Такий
вектор позначають
,
його довжина дорівнює нулю, а напрям –
довільний.
Рівними
називають вектори, які мають однакові
довжини та напрямки:
(рис. 2).
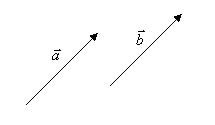
Рис. 2
Колінеарними називають вектори, які розташовані на одній прямій або паралельних прямих (рис. 3)
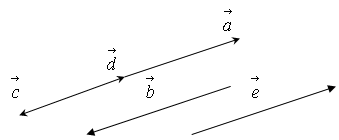
Рис. 3
Усі зображені на рис. 3 вектори – колінеарні.
Протилежними називають вектори, рівні за модулем, але протилежні за напрямом.
Вектор,
протилежний вектору
позначають
(рис. 4).
Рис. 4
Ортом
вектора
називають вектор
0,
довжина якого дорівнює одиниці, а напрям
співпадає з
,
тобто
=
0.
Компланарними називають вектори, що лежать в одній площині.
На
рис. 5 вектори
і
-
компланарні, а вектори
і
-
не є компланарними.
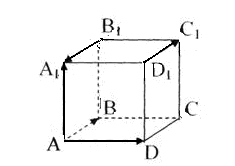
Рис. 5
В економічних дослідженнях n упорядкованих параметрів розглядають як вектор n-вимірного простору Еn.
Матриця-рядок та матриця-стовпець містять упорядковані елементи, тому їх можна розглядати як вектори простору відповідного виміру.
Наприклад,
є
Е5
є
Е4
Елементи вектора-рядка та вектора-стовпця називають координатами вектора.
Основні дії над векторами можна розглядати як геометрично, так і аналітично.
Додавання векторів
Сумою
двох
векторів
та
називають вектор
,
який сполучає початок вектора
з кінцем вектора
при умові, що початок вектора
вміщено в кінець вектора
.
Наприклад, задані вектори та (рис. 6а). Для знаходження суми цих векторів перенесли паралельно самому собі, в його кінець вмістили початок вектора та сполучили початок вектора з кінцем вектора (рис. 6б).
а) б)
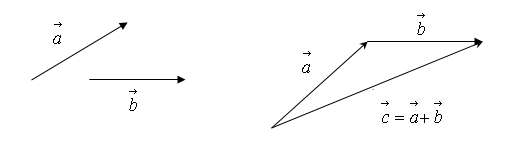
Рис. 6
Суму
кількох векторів
,
,
…
,
визначають аналогічно: початок кожного
наступного вектора вміщують в кінець
попереднього. Одержують ламану лінію
і тоді вектор, який сполучає початок
першого вектора з кінцем останнього і
є сумою цих всіх векторів.
Наведене правило додавання векторів називається правилом трикутника, а його узагальнення для кількох векторів – правилом многокутника.
Існує також правило паралелограма, згідно з яким сумою двох неколінеарних векторів, що виходять з однієї точки, є діагональ паралелограма, побудованого на цих векторах, яка виходить зі спільного початку векторів (рис.7).
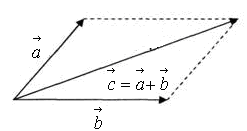
Рис. 7
Узагальненням наведеного правила є правило паралелепіпеда, згідно з яким сумою трьох некомпланарних векторів, що виходять з однієї точки, є діагональ паралелепіпеда, побудованого на цих векторах, яка виходить з цієї ж точки.
Властивості додавання векторів:
1)
—
комутативність
2)
—
асоціативність
3)
4)
Зауваження. Різницю двох векторів та будують як суму вектора та вектора (- ) (рис. 8).
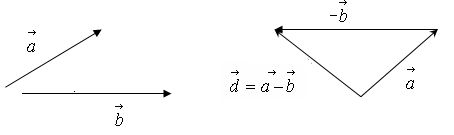
Рис. 8
Правило знаходження алгебраїчної суми векторів: координати алгебраїчної суми скінченної кількості векторів дорівнюють такій же алгебраїчній сумі відповідних координат цих векторів.
Так, у випадку алгебраїчної суми трьох векторів:
,
,
їх
алгебраїчна сума
знаходиться
за формулою
=
