Тема 14 - 15. Інтегральне числення: визначений інтеграл та його застосування

Питання для самостійної підготовки

1. Визначений інтеграл та його властивості.

2. Геометричний, фізичний, економічний зміст визначеного інтеграла.

3. Формула Ньютона-Лейбніца.

4. Використання визначеного інтеграла в економіці.

Поняття, терміни та формули, які необхідно знати

Властивості визначеного інтегралу.

Формула Ньютона-Лейбніца.

Формули для знаходження площі фігури, об’єму тіла, пройденого шляху, роботи змінної сили, обсягу виробництва за допомогою визначеного інтегралу.

Визначений інтеграл та його властивості формула ньютона-лейбніца Задачі, що приводять до поняття визначеного інтеграла

Криволінійною трапецією називається плоска фігура, що обмежена лініями:

На рис. 1. зображені: класична криволінійна трапеція (а) та її вироджені випадки (б) та (в).

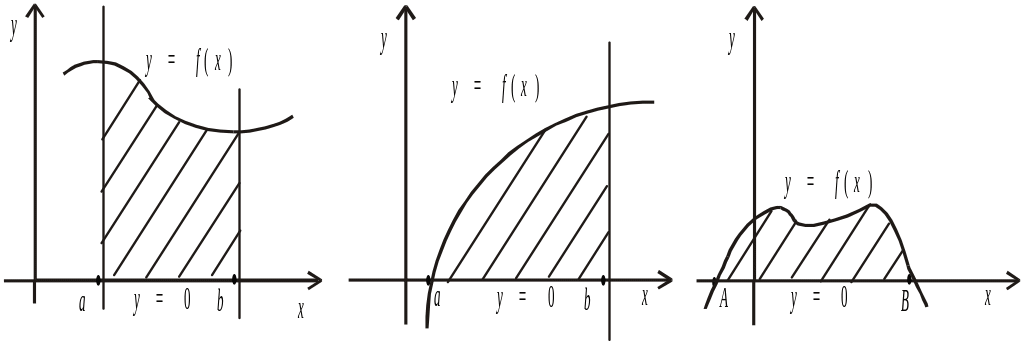
Рис. 1

Задача 1. Обчислити площу криволінійної трапеції аАВв (рис. 2).

Розв’язання. Розіб’ємо проміжок [a; b] на n частин точками так що Виберемо точки так: Побудуємо прямокутники з основою і висотою (рис. 2).

Площа елементарного прямокутника . Площа ступінчастої фігури буде тим менше відрізнятись від площі криволінійної трапеції S_aABb, чим менша довжина , а в граничному випадку ці площі будуть збігатися, тобто

Рис. 2

Задача 2. Обчислити роботу змінної сили що виконується при переміщенні матеріальної точки на проміжку (рис. 3).

Розв’язання. Розіб’ємо проміжок [a; b] на n частин точками На кожному з відрізків вважатимемо, що сила стала і дорівнює , (рис. 3).

Рис. 3

Елементарна робота сили на відрізку буде Робота А сили на відрізку [a; b] може бути знайдена так:

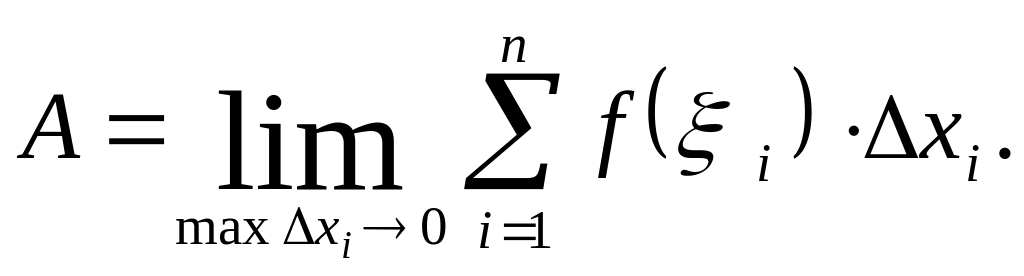
Сума типу називається інтегральною сумою.

Оперувати поняттям інтегральної суми доводиться у процесі розв’язку різних задач. Взагалі інтегральна сума може залежати від способу розбиття проміжка [a; b] на частини , а також від вибору на них точок

Поняття визначеного інтеграла

Нехай — деяка функція, що задана на проміжку [a; b]. Розіб’ємо [a; b] на n частин точками так що

Обчислимо де

Складемо інтегральну суму .

Позначимо .

Якщо існує скінченна границя інтегральних сум S_n при і не залежить ні від способу розбиття [a; b] на частини , ні від вибору точок , то ця границя називається визначеним інтегралом від функції на проміжку [a; b] і позначається:

,

де — знак визначеного інтеграла;

а, b — нижня та верхня межі інтегрування;

f(x) — підінтегральна функція;

f(x) dx — підінтегральний вираз;

dx — диференціал змінної інтегрування.

За означенням, визначений інтеграл — число, яке залежить від типу функції та проміжку [a; b]; він не залежить від того, якою буквою позначена змінна інтегрування:

Функція, для якої на [a; b] існує визначений інтеграл , називається інтегровною на цьому проміжку.

Геометричний зміст визначеного інтеграла

Якщо , то дорівнює площі відповідної криволінійної трапеції