Невизначений інтеграл та його властивості

Функція F(x) + С, що являє собою загальний вигляд всієї множини первісних для функції f(х) на проміжку I, називається невизначеним інтегралом від функції f(x) на проміжку I і позначається

(1)

де — знак невизначеного інтеграла;

f

Рис. 1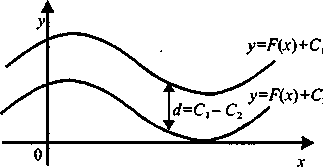

(x) — підінтегральна функція;

f(x)dx — підінтегральний вираз;

dx — диференціал змінної інтегрування.

Геометричний зміст невизначеного інтегралу полягає у тому, що функція у= F(x) + С є рівнянням однопараметричної сім'ї кривих, які одержуються одна з другої шляхом паралельного переносення вздовж осі ординат (рис. 1).

Теорема (Коші). Для існування невизначеного інтегралу для функції f(x) на певному проміжку достатньо, щоб f(x) була неперервною на цьому проміжку.

Зауваження. Виявляється, є такі невизначені інтеграли від елементарних функцій, які через елементарні функції не виражаються, наприклад, інтеграли:

існують у кожному із проміжків області визначення, але записати їх через основні елементарні функції не можна; у такому розумінні їх називають «неінтегрованими».

a) Властивості, що випливають із означення

І. Похідна від невизначеного інтеграла дорівнює підінтегральній функції

II. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.

ІІІ.

б) Властивості, що відображають основні правила інтегрування

IV. Сталий множник, що не дорівнює нулю, можна виносити з-під знака інтеграла, тобто

(2)

V. Невизначений інтеграл від суми функцій дорівнює сумі невизначених інтегралів від цих функцій, якщо вони існують, тобто

(3)

ТАБЛИЦЯ ОСНОВНИХ НЕВИЗНАЧЕНИХ ІНТЕГРАЛІВ

1. 2. 3.

4. 5. 6.

7. 8.

9.

11.

13.

15.

16.

17.

18.

19.

20.

21.

Метод безпосереднього інтегрування

Цей метод базується на властивостях невизначеного інтеграла. Мета методу — розкласти підінтегральну функцію на такі доданки, інтеграли від яких відомі або їх простіше інтегрувати, ніж початкову підінтегральну функцію.

Приклад.

Метод підстановки (заміна змінної інтегрування)

Суть методу підстановки полягає у перетворенні інтегралу в інтеграл , який обчислюється безпосереднім інтегруванням.

Для перетворення підінтегрального виразу потрібно ввести нову функцію . Диференціюючи цю рівність, отримаємо , звідси, 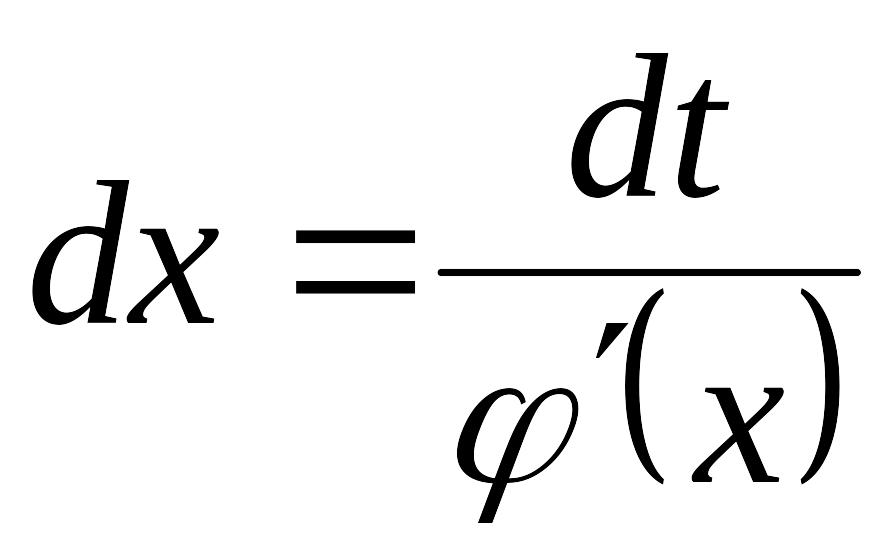. Підставивши в підінтегральний вираз замість та їх значення, одержимо інтеграл від нової змінної .

Проінтегрувавши, необхідно повернутись до заміни, тобто підставити замість функції її вираз. Цей метод доцільно використовувати, коли підінтегральна функція є складною.

Приклад 1. Знайти невизначений інтеграл .

Скористаємось підстановкою ; та формулою інтегрування .

Приклад 2. Знайти невизначений інтеграл .

Скористаємось підстановкою ; та формулою інтегрування степеневої функції х^п при .

Питання для самоперевірки

Дайте означення первісної та невизначеного інтегралу.

Сформулюйте основні властивості невизначеного інтегралу.

Запишіть таблицю основних невизначених інтегралів.

Вкажіть суть методів безпосереднього інтегрування та заміни змінних у невизначеному інтегралі.

Завдання

Знайдіть інтеграли: ; .

Наведіть приклади інтегралів, знайдених:

безпосередньо;

методом підстановки (заміни змінної).

Рекомендована література

1. Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.:ЦУЛ, 2010. – С. 268-277.

2. Васильченко І.П. Вища математика для економістів: Підручник. – К.: Знання – Прес, 2002. – С. 284-288.

3. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер и др. – М.: ЮНИТИ, 1999. – С. 251-256.

4. Бугір М.К. Математика для економістів. – Тернопіль, 1998. – С. 269-271.

5. Математика для економістів: теорія та застосування./ Лавренчук В.П. та ін. - К.: Кондор, 2007. – С. 137 – 140.

6. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навч. посібник. – К.:ЦУЛ, 2005. – С. 222-228.

7. Богомолов М.В. Практичні заняття з математики, 1990. – С. 188-194.

8. Богомолов Н.В., Сергиенко Л.Ю. Сборник дидактических заданий по математике. – М.: Высш.шк., 1987. – С. 99-101.