Застосування функцій багатьох змінних в економічній теорії

Аналогічно поняттю еластичності функції однієї змінної ми можемо ввести поняття частинних еластичностей функції двох змінних.

Припустимо, що функції і виражають попит на товари і , який залежить від ціни на ці товари. Частинні еластичності попиту відносно цін і подаються у вигляді:

, ,

, .

Частинна еластичність попиту на товар відносно ціни товару приблизно означає відсоток підвищення (або зниження) попиту на товар , якщо ціна товару зростає на 1%, а товару залишається незмінною.

Частинна еластичність попиту на товар відносно ціни товару приблизно означає відсоток підвищення (або зниження) попиту на товар , якщо ціна товару зростає на 1%, а товару залишається без змін, і т. ін.

Приклад. Припустимо, що функція попиту на товар є

.

Знайти частинні показники еластичностей.

 Розв’язання. Маємо , .

Для , дістаємо .

Це означає, що коли ціна товару зростає на 1%, а товару залишається без змін, тоді попит на товар знижується на 0,3%. Далі, , тобто якщо ціна товару зростає на 1% при незмінній ціні товару , попит на товар зростає приблизно на 0,05%.

Питання для самоперевірки

Дайте означення границі функції двох змінних, вкажіть основні властивості границь.

Яким чином означується функція двох змінних, неперервна в точці та в області?

Сформулюйте алгоритм знаходження найбільшого і найменшого значення функції двох змінних в замкненій області.

Наведіть приклади застосування функції двох змінних в економічній теорії.

Завдання

Наведіть приклади:

знаходження границі функцій багатьох змінних;

дослідження функції двох змінних на неперервність.

Знайдіть найбільше і найменше значення функції у замкненій області, що обмежена прямими , , .

Знайдіть найбільше і найменше значення функції у колі .

Рекомендована література

Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.:ЦУЛ, 2010. – С. 242-243, 251-252, 257-262.

Бугір М.К. Математика для економістів. – Тернопіль, 1998. – С. 242 – 246; 254 – 257.

Васильченко І.П. Вища математика для економістів: Підручник. – К.: Знання – Прес, 2002. – С. 341-347; 363-369.

Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навч. посібник. – К.:ЦУЛ, 2005. – С. 196-201, 218-220.

Тема 12 - 13. Інтегральне числення: невизначений інтеграл

Питання для самостійної підготовки

Первісна та її властивості.

Невизначений інтеграл та його властивості.

Таблиця основних невизначених інтегралів.

Методи інтегрування: безпосереднє інтегрування, інтегрування методом заміни змінної.

Поняття, терміни та формули, які необхідно знати

Первісна функції.

Невизначений інтеграл та його властивості.

Таблиця невизначених інтегралів.

Безпосереднє інтегрування.

Інтегрування методом підстановки (заміни змінної).

Первісна функції та її властивості

Функція F(x) називається первісною для функції f(x) на проміжку І, якщо на цьому проміжку F'(x) = f(x) або dF(x) = f(x)dx .

Із означення виходить, що первісна F(x) — диференційована, а значить неперервна функція на проміжку І, і її вигляд суттєво залежить від проміжку, на якому вона розглядається.

Приклад: Первісні для функції мають вигляд:

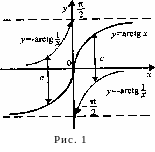
причому, F₁(x), F₂(x) — неперервні R, a F₃(x) у точці х = 0 має розрив (рис. 1). У цьому прикладі первісні F_i(x) і = 1,2,3, знайдені методом підбору із на­ступною перевіркою, використо-вуючи таблицю похідних функцій.

Теорема (про множину первісних). Якщо F(x) — первісна для функції f(х) на проміжку I, то

1) F(x) + C — також первісна для f(x) на проміжку I;

2) будь-яка первісна Ф(х) для f(x) може бути представлена у вигляді Ф(х) = F(x) + С на проміжку I. (Тут С = const називається сталою інтегрування).

Наслідок. Дві будь-які первісні для однієї й тієї самої функції на проміжку I відрізняються між собою на сталу величину (рис. 1).

Операція знаходження первісних для функції f(x) називає­ться інтегруванням f(x).

Задача інтегрування функції на проміжку полягає у тому, щоб знайти всі первісні функції на цьому проміжку, або довести, що функція не має первісних на цьому проміжку.

Для розв'язання задачі інтегрування функції достатньо знайти одну будь-яку первісну на розглядуваному проміжку, наприклад F(x), тоді (за теоремою про множину первісних) F(x) + С — загальний вигляд усієї мно­жини первісних на цьому проміжку.