Неперервність функції двох змінних

Функція називається неперервною в точці , якщо .

Функція називається неперервною в області (замкненій чи відкритій), якщо вона неперервна в кожній точці цієї області.

Приклад 1. Розглянемо функцію двох незалежних змінних

Ця функція має розрив у точці (0; 0), бо в точці для функції границі не існує (див. приклад).

Приклад 2. Точки розриву можуть бути не тільки ізольованими, як у попередньому прикладі, а й заповнювати лінії, поверхні і т. п. Так, функції двох змінних , мають розриви: перша — прямі , друга — окіл .

Для функції трьох змінних , розриви заповнюють у першому випадку гіперболічний параболоїд , а в другому — конус .

Нехай функція визначена на множині Е, а змінні x і y, у свою чергу, залежать від змінних u та v і , , де обидві функції та визначені на множині D. Якщо для будь-якого значення , такі, що (рис. 3), то кажуть, що на множині D визначена складна функція , де , ; x, y — проміжні змінні, u, v — незалежні змінні.

Рис. 3.

Приклад. Функція , де , — складна функція. Вона визначена на координатній площині. Її можна записати у вигляді .

Теорема. Нехай на множині D визначено складну функцію , де , , і нехай функції , неперервні в точці , а функція неперервна в точці , де , . Тоді складна функція неперервна в точці .

Властивості неперервної функції двох змінних

Якщо функція неперервна в точці, то вона обмежена деяким околом цієї точки.

Якщо функції та неперервні в точці , то в цій точці будуть неперервними , , при .

Якщо функція неперервна на замкненій обмеженій множині, то вона обмежена на цій множині.

Якщо функція неперервна на замкненій обмеженій множині, то серед її значень на цій множині є як найменші, так і найбільші.

Нехай функція неперервна на зв’язаній множині D і набуває у двох точках А і В цієї множини значень різних знаків. Тоді у множині D знайдеться така точка, що в ній функція перетворюється на нуль.

Нехай функція неперервна на зв’язаній множині D й у двох будь-яких точках А та В цієї множини набуває нерівних значень та . Тоді на цій множині вона набуває будь-яких значень , яке лежить між і , тобто існує така точка , що .

Найбільше та найменше значення функції двох змінних в замкненій області

Функція, що неперервна на замкненій обмеженій множині , досягає на ній найбільшого та найменшого значень. Цих значень вона може набувати як у внутріш­ніх точках множини (кожна така точка є точкою екстремуму функції, у цій точці перші частинні похідні дорівнюють нулю або не існують), так і на її межі, тобто необхідне спеціальне дослідження межових точок множини .

Приклад. Знайдемо найбільше та найменше значення функції в області, обмеженій прямими , , , .

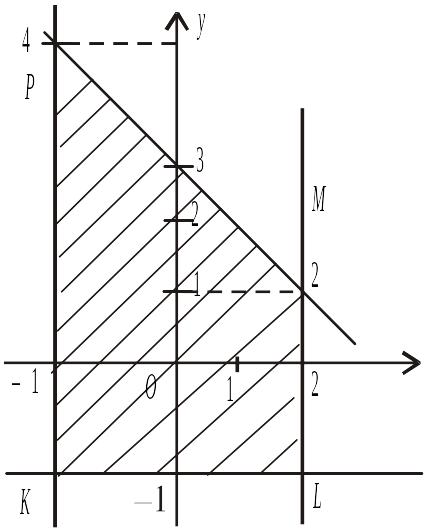
1. Дослідимо поводження функції всередині області KLMP. Знайдемо перші частинні похідні функції : , . Прирівнявши їх до нуля, дістанемо стаціонарні точки та .

2. Дослідимо поводження функції на межі області. Відрізок має рівняння , . Підставивши у задану функцію, дістанемо . Треба знайти найбільше та найменше значення цієї функції на відрізку .

Маємо , отже, функція зростає і тому досягає найбільшого значення на кінцях відрізка, тобто в точках і .

Відрізок має рівняння , . Підставивши у задану функцію, дістанемо функцію z як функцію від змінної у: . Маємо на відрізку .

Отже, функція досягає найбільшого та найменшого значень на кінцях відрізка, тобто в точках і .

Відрізок має рівняння , . Підставивши у задану функцію, дістанемо функцію z як функцію від змінної х: , тобто . Маємо , звідки при . Отже, на відрізку функція може досягати найбільшого та найменшого значень у точках , та .

Відрізок має рівняння , . Підставивши у задану функцію, дістанемо . Маємо , отже, функція досягає найбільшого та найменшого значень на кінцях відрізка, тобто в точках , .

Таким чином, функція може досягти найбільшого та найменшого значень тільки в таких точках: , , , , , , .

Знаходимо , , , , , , . Отже, , і це значення досягається в точці , , і це значення досягається в точці .