Питання для самоперевірки

1. Дайте означення похідної функції.

2. Запишіть правила диференціювання і таблицю похідних елементарних функцій.

3. Сформулюйте геометричний та фізичний зміст похідної. Наведіть приклади застосувань похідної в економіці, геометрії, фізиці, механіці та інших дисциплінах.

4. Сформулюйте означення критичних точок функції.

5. Вкажіть достатні ознаки зростання і спадання функції.

6. Опишіть алгоритм знаходження найбільшого та найменшого значення функції на відрізку.

7. Наведіть приклад розв’язування задачі на максимум (мінімум) прикладного змісту.

Завдання

1. Знайдіть похідні функцій:

1. 

1. 

2. 

3. .

4. 

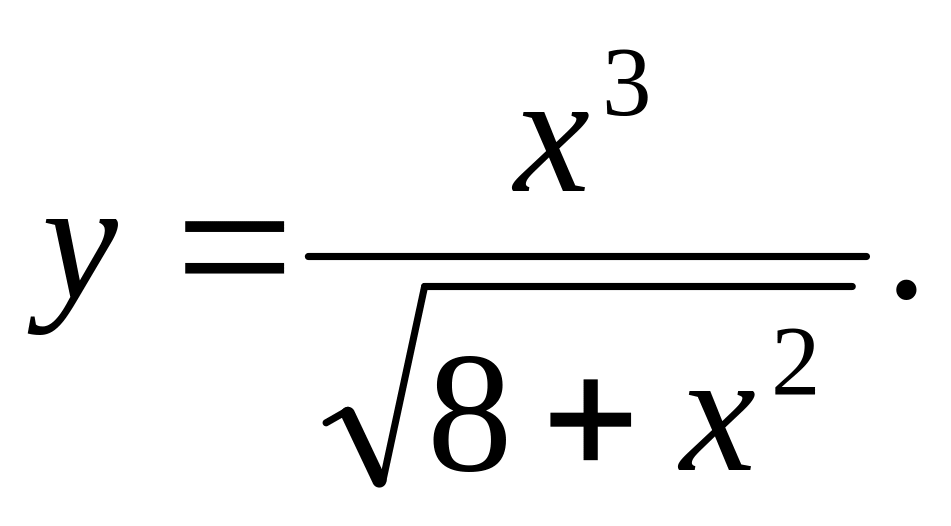
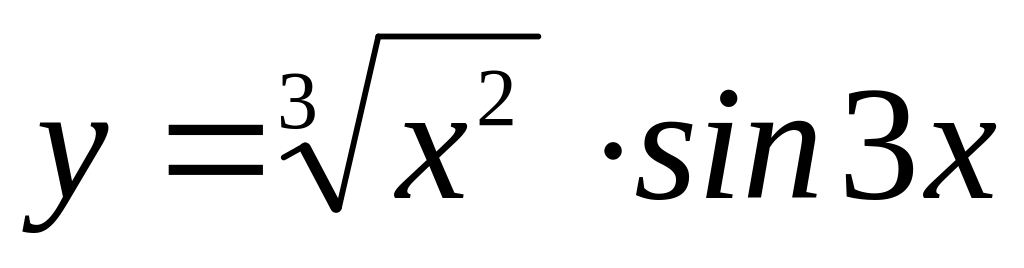2. Дослідіть функцію і побудуйте її графік:

3. Знайдіть найбільше і найменше значення функції на проміжку .

4. Тіло рухається прямолінійно за законом . Визначте швидкість і прискорення руху тіла в момент часу

5. Складіть рівняння дотичної і нормалі до кривої в точці з абсцисою

Рекомендована література

1. Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.:ЦУЛ, 2010. – С. 200-203, 205-225, 233-236.

2. Богомолов М.В. Практичні заняття з математики, 1990. – С. 92 – 107, 111 – 113.

3. Богомолов Н.В., Сергиенко Л.Ю. Сборник дидактических заданий по математике. – М.: Высш.шк., 1987. – С. 88 – 96.

4. Васильченко І.П. Вища математика для економістів: Підручник. – К.: Знання – Прес, 2002. – С. 217 – 228, 234 – 238.

5. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер и др. – М.: ЮНИТИ, 1999 - С. 176 – 192, 202 – 206, 216 -217, 224 - 225.

6. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навч. посібник. – К.:ЦУЛ, 2005. – С. 161-166, 181-186.

7. Математика для економістів: теорія та застосування / Лавренчук В.П. та ін. - К.: Кондор, 2007. – С. 105 – 111, 116 – 120.

Тема 9 -11. Диференціальне числення функції багатьох змінних

Питання для самостійної підготовки

1. Границя та неперервність функції багатьох змінних, їх властивості.

2. Найбільше, найменше значення функції багатьох змінних в замкненій області.

3. Застосування функцій багатьох змінних в економічній теорії.

Поняття, терміни та формули, які необхідно знати

Границя функції двох змінних, властивості границь.

Неперервність функції двох змінних, властивості неперервних функцій.

Найбільше, найменше значення функції багатьох змінних в        замкненій області.

Застосування функцій багатьох змінних в економічній теорії

Границя функції двох змінних

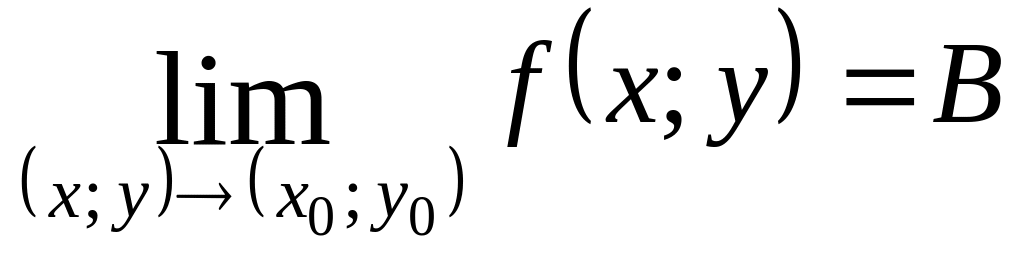Число B називається границею функції при , , якщо для будь-якого існує число таке, що при виконанні нерівності виконується нерівність і позначається або .

Зауваження. Для функції багатьох змінних справедливі теореми про границю суми, добутку та частки, які анало- гічні відповідним теоремам для функції однієї незалежної змінної.

Наведемо формулювання відповідних теорем.

Теорема 1. Якщо функція має границю при , то ця границя єдина.

Теорема 2. Якщо функція має границю при , то ця функція обмежена в деякому околі точки .

Теорема 3. Якщо , і в деякому околі точки виконується нерівність , то .

Теорема 4. Нехай , . Тоді:

1)  ;

2)  ;

3)  .

Приклад. Обчислити .

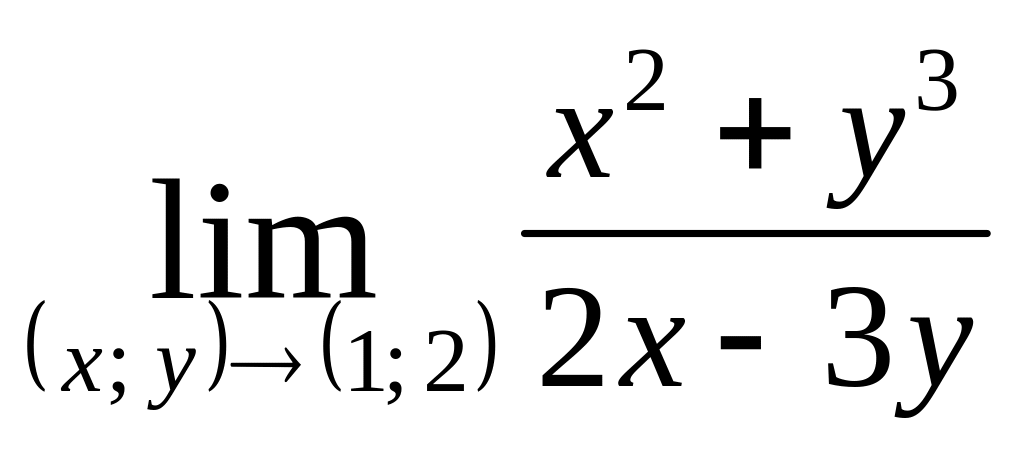 Розв’язання. Згідно з теоремами про арифметичні операції з грани- цями, а також те, що границя сталої дорівнює сталій, тобто , , маємо .

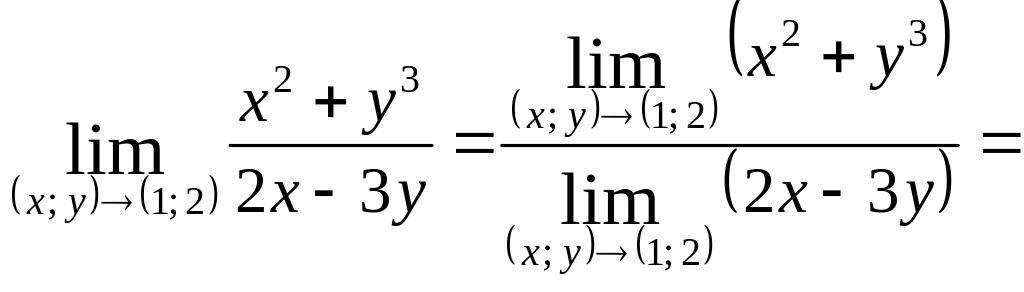
Зауваження. Між поняттями границі в точці для функції однієї змінної та функції багатьох змінних є багато спільного, але є й принципова відмінність, яка робить поняття границі функції кількох змінних суттєво більш обмеженим, ніж поняття границі функції однієї змінної.

Річ у тім, що коли ( — функція однієї змінної), то це означає, що і лівостороння і правостороння границі дорівнюють b. Правильним є й обернене: з існування та збігу двох односторонніх границь випливає існування границі функції в точці.

Для функції двох змінних наближатися до точки можна нескінченною множиною способів: і справа, і зліва, і зверху, і знизу, і під кутом 30 до осі Ох тощо (рис. 1).

Рис. 1 Рис. 2

Більше того, до точки можна наближатися не тільки по прямій, а й по більш складних траєкторіях (рис. 2).

Очевидно, що рівність 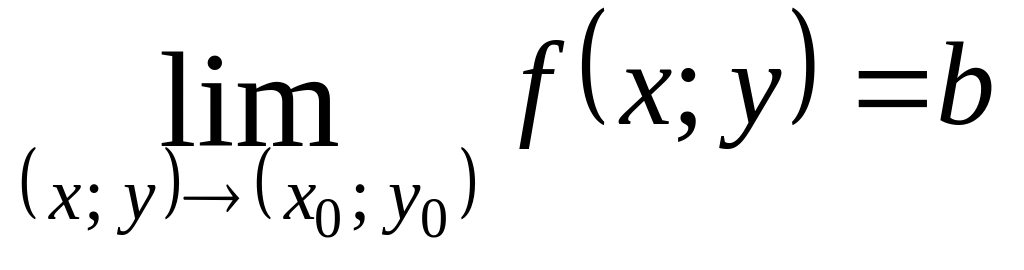правильна тоді й тільки тоді, коли границя дорівнює b при наближенні до точки по будь-якій траєкторії. Це суттєво більш обмежене, ніж збіг двох односторонніх границь у випадку функції однієї змінної.

Приклад. Довести, що не існує.

Будемо наближатися до точки (0; 0) по прямій . Якщо , тоді .

Зауважимо, що значення границі залежить від кутового коефіцієнта прямої, наприклад:

при границя дорівнює ; при границя дорівнює і т. п.

Таким чином, якщо наближатися до точки (0; 0) з різ- них напрямків, то дістанемо різні значення, тобто границя не існує.