Застосування похідної функції для знаходження рівняння дотичної і нормалі

Нехай маємо функцію , диференційовану в точці , задану графічно (рис. 3).

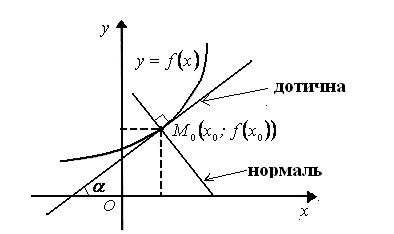
Рис. 3.

Дотична до графіка функції в точці М₀ є граничним положенням січної М₀М, коли точка М необмежено наближається до М₀, рухаючись вздовж графіка функції:

(2)

Відповідно до геометричного змісту похідної: f’(x₀)=k – кутовий коефіцієнт дотичної, який дорівнює значенню похідної в точці х₀, тобто тангенс кута нахилу дотичної до доданого напрямку осі абсцис.

Нормаль до графіка функції в точці М₀ – це пряма, що проходить через точку М₀ і перпендикулярна до дотичної, проведеної в цій точці:

(3)

Кутовий коефіцієнт нормалі при цьому . Формула (5) має місце, якщо f’(x₀) 0 тобто дотична не паралельна осі Ох. В іншому випадку нормаль паралельна осі Оу, і тоді рівняння нормалі:

х-х₀=0 (4)

Приклад 1. Знайти рівняння дотичної і нормалі до графіка функції у точці з абсцисою х₀=3.

Розв’язання. Знайдемо похідну функції, значення функції та її похідної в точці х₀:

.

Скориставшись рівнянням дотичної (2), матимемо , звідси - шукане рівняння дотичної.

Запишемо тепер рівняння нормалі, відповідно до формули (3): , звідси - шукане рівняння нормалі.

Відповідь: - рівняння дотичної; - рівняння нормалі.

Приклад 2. Який кут з віссю абсцис утворює дотична до параболи y=x²-4x+8 у точці (3;5)?

Розв’язання. Безпосередньо підстановкою координат заданої точки в рівняння параболи переконуємося, що вона їй належить.

Знайдемо похідну функції, що задає параболу y=2x-4.

Тоді, згідно з геометричним змістом похідної: . Звідси, , а отже, шуканий кут .

Відповідь: .

Приклад 3. Дотична до графіка функції нахилена до осі абсцис під кутом . Знайти координати точки дотику.

Розв’язання. Знайдемо похідну функції: . За умовою y(x₀)=tg =1. Підставивши значення похідної в точці, знайдемо абсцису точки дотику: , звідси, . Знайдемо ординату точки дотику, підставивши у формулу, що задає функцію: .

Отже, дотична до параболи проведена в точці (2;2).

Відповідь: (2;2).

Фізичні та механічні застосування похідної

Нехай матеріальна точка рухається прямолінійно, а закон її руху задано деякою функцією: S=S(t). Поставимо задачу: знайти швидкість точки у момент часу t. Враховуючи, що миттєва швидкість є границею середньої швидкості за достатньо малий проміжок часу t, одержимо:

.

Таким чином, похідною від пройденого шляху за часом є миттєва швидкість:

(5)

Аналогічно, шукаючи миттєве прискорення, як швидкість зміни швидкості v=v(t) у момент часу t, матимемо формулу:

.

Звідси, похідною від швидкості за часом є миттєве прискорення:

(6)

Похідна дає можливість знайти силу, що діє на тіло у певний момент часу за другим законом Ньютона:

(7)

У формулі (9) миттєве прискорення є другою похідною від шляху за часом, у цьому полягає фізичний зміст другої похідної.

Для знаходження кінетичної енергії тіла у певний момент часу може бути використана формула: , причому швидкість знаходиться за формулою (7).

Оскільки похідна виступає, як швидкість зміни деякої функції, її використовують, наприклад, для знаходження сили змінного струму, який проходить через поперечний переріз провідника у момент часу t:

(8)

У формулі (10) - величина заряду, що проходить через поперечний переріз провідника у момент часу t.

Приклад 1. Матеріальна точка рухається прямолінійно за законом (м). Знайти швидкість і прискорення матеріальної точки у момент часу с.

Розв’язання.

За формулою (5) знайдемо миттєву швидкість матеріальної точки: , звідси (м/с).

Для знаходження миттєвого прискорення скористаємось формулою (6): , звідси, (м/с²).

Відповідь: 104 м/с; 50 м/с².

Приклад 2. Тіло масою 100 кг рухається прямолінійно за законом (м). Знайти кінетичну енергію тіла через 2 с після початку руху.

Розв’язання. Знайдемо миттєву швидкість тіла за формулою (5): , звідси, (м/с). Підставивши знайдену швидкість у формулу кінетичної енергії , одержимо: Дж, або кДж.

Відповідь: 20 кДж.

Приклад 3. Заряд, що проходить через поперечний переріз провідника у момент часу t (c), змінюється за законом (Кл). Знайти силу струму у момент часу с.

Розв’язання. Використавши формулу (8), матимемо значення змінної сили струму: , звідси (А).

Відповідь: А.

Приклад 4. Тіло масою (кг) рухається прямолінійно за законом (м), де - сталі. Довести, що сила, яка діє на тіло, стала.

Розв’язання. Використавши формулу (7), покажемо, що . Для цього знайдемо миттєве прискорення тіла: ; . Таким чином, . Тоді , тобто рух тіла відбувається під дією сталої сили, що й потрібно було довести.