Найбільше і найменше значення функції

НА ВІДРІЗКУ

Нехай дано функцію , яка неперервна на відрізку [a;b], диференційована в інтервалі (a;b), за винятком, можливо, скінченого числа точок, де вона не існує. Необхідно ж знайти найбільше та найменше значення функції на цьому відрізку. Як відомо з математичного аналізу, функція, яка неперервна на відрізку, набуває на ньому свого найбільшого і найменшого значення.

Чим викликана необхідність знаходження найбільшого і найменшого значення функції на відрізку?

Справа в тому, що в практичних задачах, де процес, явище, закон, величина описуються певною функцією, зміст самої задачі накладає певні обмеження на аргумент, тобто аргумент має певні межі.

Так, наприклад, кут трикутника може змінюватися лише від 0 до , швидкість тіла доводиться розглядати в проміжку часу від t₀ до t₁ тощо. Тому й необхідно досліджувати поведінку функції на конкретному проміжку [a;b].

Щоб знайти найбільше і найменше значення функції на відрізку [a;b], необхідно виконати такі кроки:

1. Знайти критичні точки функції ; для цього знайти похідну функції і прирівняти її до нуля (а також вказати внутрішні точки області визначення, в яких похідна не існує).

2. Знайти значення функції у тих критичних точках, які належать інтервалу (a;b), а також на кінцях відрізка, тобто .

3. Серед усіх значень вибрати найбільше і найменше значення, позначивши їх відповідно та .

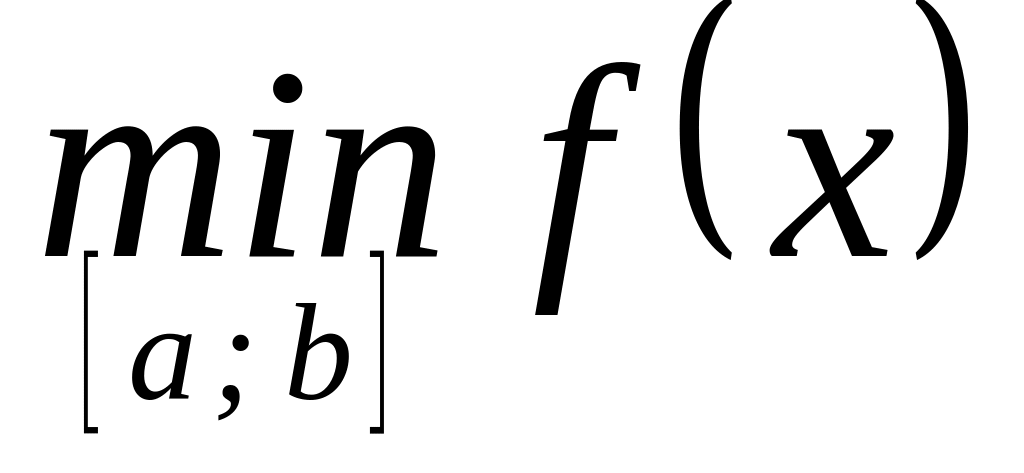У випадку, коли функція монотонна на відрізку [a;b], то найбільшого і найменшого значення вона досягає на кінцях відрізка. У цьому випадку слід обмежитись обчисленням значень .

Приклад 1. Знайти найбільше та найменше значення функції на відрізку [-2;2].

Розв’язання. На даному відрізку функція визначена і неперервна, диференційована в інтервалі (-2;2).

Знайдемо похідну функції та її критичні точки:

.

Похідна функції визначена в усіх точках заданого інтервалу, оскільки і . З рівняння маємо, що , звідси х=0.

Знайдемо значення функції в критичній точці і на кінцях відрізка: .

Порівнюючи одержані значення, знаходимо найбільше і значення функції на відрізку: ; .

Відповідь: ; .

Приклад 2. Знайти найбільше та найменше значення функції на відрізку [-1;1].

Розв’язання. Функція визначена і неперервна на відрізку , диференційована в інтервалі (-1;1). Тому вона набуває на даному відрізку найбільшого і найменшого значення. Знайдемо критичні точки даної функції. Для цього знайдемо похідну і прирівняємо її до нуля. З рівняння х⁴+8х=0; або маємо: х=0; х=-2.

Так як ; , то на інтервалі (-1;1) функція має лише одну критичну точку. Знайдемо значення функції в цій точці: .

Обчислимо значення функції на кінцях відрізка: , .

Порівнюючи одержані значення, знаходимо найбільше і значення функції на відрізку: ; .

Відповідь: ; .

Застосування похідної в економічній теорії

Розглянемо задачу про продуктивність праці. Нехай функція и = и(t) відображає кількість виробленої продукції u за час t i необхідно знайти продуктивність праці в момент t₀.

За період часу від t₀ до t₀ + t кількість виробленої продукції зміниться від значення u₀=u(t₀) до значення u₀+ u=u(t₀+ t); тоді середня продуктивність праці за цей період часу z_сер= . Очевидно, що продуктивність праці в момент t₀ можна визначити, як граничне значення середньої проду­ктивності за період часу від t₀ до t₀ + t при , тобто

Таким чином, продуктивність праці є похідна від обсягу виробленої продукції по часу.

Розглянемо ще одне поняття, яке ілюструє економічний зміст похідної.

Витрати виробництва y будемо розглядати як функцію кількості проду­кції х, що виробляється. Нехай х — приріст продукції, тоді y — приріст витрат виробництва і - середній приріст витрат виробництва продукції на одиницю продукції.

Похідна у' = — виражає граничні витрати виробництва і характеризує наближено додаткові затрати на виро­бництво одиниці додаткової продукції.

Граничні витрати залежать від рівня виробництва (кількість продукції, що випускається) х і визначаються не постійними виробничими затратами, а лише змінними (на сировину, паливо та ін.). Аналогічним чином можуть бути визначені гранична виручка, граничний доход, граничний продукт, гранична корисність, гранична продуктивність та інші граничні величини.

Для дослідження економічних процесів та розв’язання інших прикладних задач використовується поняття еластичності функції.

Еластичністю функції Е_x(y) називається границя відношення відносного приросту функції у до відносного приросту змінної х при х 0:

(1)

Еластичність функції наближено відображає, на скільки відсотків змі­ниться функція у = f (х) при зміні незалежної змінної х на 1%.

Визначимо геометричний зміст еластичності функції. За означенням , де — тангенс кута нахилу дотичної в точці М (x, у) (рис. 1, 2).

Враховуючи, що з трикутника MBN MN = х , MC = y, а з подібності трикутників MBN та АМС , тобто еластичність функції (за абсолютною величиною) дорівнює відношенню відстаней по дотичній від даної точки графіка функції до точок її перетину з осями Ох та Оу. Якщо точки перетину дотичної до гра­фіка функції А і В знаходяться по одну сторону від точки М, то еластич­ність Е_х (у) додатна (рис. 1), якщо по різні сторони, то Е_х(у) від’ємна (рис. 2).

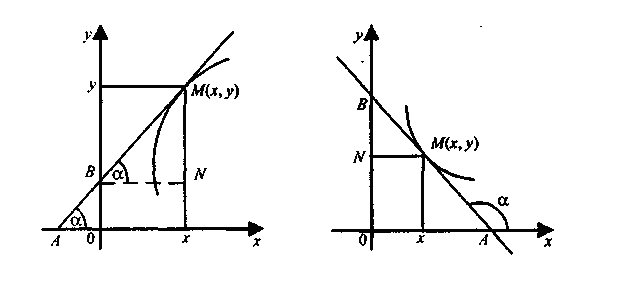
Рис.1. Рис.2.

Еластичність функції застосовується при аналізі попиту та пропозиції. Наприклад, еластичність попиту у відносно ціни х (або доходу х) — коефі­цієнт, що визначається за формулою (1) і наближено відображає, на скільки відсотків зміниться попит (обсяг пропозиції) при зміні ціни (або доходу) на 1%.

Якщо еластичність попиту (за абсолютною величиною) , то попит вважають еластичним, якщо — нееластичним відносно ці­ни (або доходу). Якщо , то мова йде про попит з одиничною еластичністю.

Приклад 1. Залежність між витратами виробництва у і обсягом продукції х, що випускається, визначається функцією у = 50х - 0,05х³ (грош. од.). Визначити середні та граничні витрати за умови, що обсяг продукції 10 одиниць.

Розв'язання. Функція середніх витрат (на одиницю продукції) виражаєть­ся відношенням при х = 10 середні витрати (на одиницю продукції) дорівнюють (грош. од.). Функ­ція граничних витрат виражається похідною у'(x) = 50-0,15x² ; при х = 10 граничні витрати складають у'(10) = 50-0,15·10² =35 (грош. од.). Отже, як­що середні витрати на виробництво одиниці продукції складають 45 грош. од., то граничні витрати, тобто додаткові затрати на виробництво додатко­вої одиниці продукції за умови даного рівня виробництва (обсягу продук­ції, що випускається 10 од.), складають 35 грош. од.

Приклад 2. Залежність між собівартістю одиниці продукції у (тис. грош. од.) та випуском продукції х (млрд. грош. од.) виражається функцією у=0,5х+80. Знайти еластичність собівартості за умови випуску продукції в розмірі 60 млрд. грош. од.

Розв’язання. За формулою (1) еластичність собівартості

При х = 60 , тобто при виробництві продукції в розмірі 60 млрд. грош. од., збільшення її на 1% викличе зменшення собівартості на 0,6%.

Приклад 3. Експериментально були встановлені функції попиту та пропозиції , де q та s — кількість товарів, що відповідно купується і пропонується для продажу за одиницю часу, р — ціна това­ру. Знайти: а) рівноважну ціну, тобто ціну, за якої попит та пропозиція врі­вноважуються; б) еластичність попиту та пропозиції для цієї ціни; в) зміну доходу при збільшенні ціни на 5% від рівноважної.

Розв'язання. а) Рівноважна ціна визначається з умови q = s, , звідки р = 2, тобто рівноважна ціна дорівнює 2 грош. од.

б) Знайдемо еластичності попиту та пропозиції за формулою (1):

Для рівноважної ціни р = 2 маємо Е_р(q)=-0,3, E_p(s) = 0,8.

Так як отримані значення еластичності за абсолютною величиною ме­нші 1, то попит і пропозиція даного товару за рівноважної (ринкової) ціни нееластичні відносно ціни. Це означає, що зміна ціни не приведе до різкої зміни попиту та пропозиції. Так, при збільшенні ціни p на 1% попит змен­шиться на 0,3%, а пропозиція збільшиться на 0,8%.

в) При збільшенні ціни р на 5% від рівноважної попит зменшиться на величину 50,3 = 1,5%, тобто прибу­ток зросте на 3,5%.