
- •Спеціальності:
- •5.03050901 “Бухгалтерський облік”
- •Тема 1. Елементи лінійної алгебри
- •Системи т рівнянь з п невідомими
- •Ранг матриці
- •Критерій сумісності системи лінійних рівнянь – теорема кронекера-капеллі
- •Прикладні задачі курсів спецдисциплін, які приводять до систем лінійних рівнянь та їх розв’язування
- •Тема 2. Елементи векторної алгебри
- •Основні поняття, лінійні операції над векторами
- •Додавання векторів
- •Множення вектора на число
- •Розкладання вектора за базисом
- •Прямокутна декартова система координат
- •Проекція вектора на вісь координати вектора на площині та в просторі
- •Векторний добуток векторів
- •Властивості векторного добутку
- •Застосування векторного добутку
- •Мішаний добуток векторів
- •Знаходження мішаного добутку в координатній формі
- •Властивості мішаного добутку
- •Кут між векторами умови колінеарності та компланарності векторів Кут між векторами
- •Умова колінеарності векторів
- •Умова компланарності векторів
- •Питання для самоперевірки
- •Тема 3. Аналітична геометрія: Пряма і площина в просторі
- •Пряма в просторі
- •Співвідношення між прямими і площинами
- •Питання для самоперевірки
- •Теми 4-5. Вступ до математичного аналізу: функція, границя і неперервність функції
- •Поняття функції, область визначення, способи задання
- •Основні елементарні функції, їх властивості і графіки
- •Перетворення графіків функцій
- •Застосування функцій в економіці
- •Неперервність функції в точці та на відрізку
- •Точки розриву функції, їх класифікація
- •Основні теореми про неперервні функції
- •Питання для самоперевірки
- •Тема 6 - 8. Диференціальне числення функції однієї змінної: похідна та її застосування
- •Поняття похідної функції в точці, її фізичний та геометричний зміст
- •Правила диференціювання
- •Похідна складеної функції
- •Похідні вищих порядків
- •Зростання, спадання функції достатня умова монотонності
- •Екстремум функції. Необхідна та достатня умови існування екстремуму функції. Поняття критичних точок та точок екстремуму функції
- •Необхідна та достатня умова екстремуму
- •Найбільше і найменше значення функції
- •Застосування похідної в економічній теорії
- •Застосування похідної функції для знаходження рівняння дотичної і нормалі
- •Фізичні та механічні застосування похідної
- •Питання для самоперевірки
- •Тема 9 -11. Диференціальне числення функції багатьох змінних
- •Границя функції двох змінних
- •Неперервність функції двох змінних
- •Властивості неперервної функції двох змінних
- •Найбільше та найменше значення функції двох змінних в замкненій області
- •Застосування функцій багатьох змінних в економічній теорії
- •Питання для самоперевірки
- •Тема 12 - 13. Інтегральне числення: невизначений інтеграл
- •Первісна функції та її властивості
- •Невизначений інтеграл та його властивості
- •І. Похідна від невизначеного інтеграла дорівнює підінтегральній функції
- •Метод безпосереднього інтегрування
- •Метод підстановки (заміна змінної інтегрування)
- •Питання для самоперевірки
- •Тема 14 - 15. Інтегральне числення: визначений інтеграл та його застосування
- •Визначений інтеграл та його властивості формула ньютона-лейбніца Задачі, що приводять до поняття визначеного інтеграла
- •Поняття визначеного інтеграла
- •Геометричний зміст визначеного інтеграла
- •Формула Ньютона—Лейбніца
- •Властивості визначеного інтеграла
- •Застосування визначеного інтегралу для обчислення об’ємів, шляху Обчислення об’єму тіла за площами його поперечних перерізів
- •Обчислення об’єму та площі поверхні тіла обертання
- •Обчислення пройденого шляху
- •Використання визначеного інтегралу в економіці
- •Питання для самоперевірки
- •Богомолов н.В., Сергиенко л.Ю. Сборник дидактических заданий по математике. – м.: Высш.Шк., 1987. – с. 107-109.
- •Тема 16 -18. Диференціальні рівняння
- •Диференціальні рівняння у повних диференціалах
- •Диференціальні рівняння, що допускають зниження порядку
- •Задачі на складання диференціальних рівнянь економічного змісту
- •Питання для самоперевірки
Правила диференціювання
Теорема (похідна суми та різниці диференційованих функцій): Якщо функції u=u(x) і v=n(x) мають похідні у всіх точках інтервалу (a; b), то (u(x)±v(x))´= u´(x)±n´(x) для будь-якого х є (a; b).
Приклад
а)
![]()
б)
![]()
в)
![]()
Зауваження. Методом математичної індукції доводиться справедливість формули похідної алгебраїчної суми для скінченного числа складових.
Теорема
(похідна добутку диференційованих
функцій).
Якщо
функції u(x) і n(x)
мають похідні у всіх точках інтервалу
(a; b), то
![]() для
будь-якого х є (a; b).
для
будь-якого х є (a; b).
Приклад
а)
![]()
![]()
б)
![]()
в)
![]()
Наслідок. Сталий множник можна виносити за знак похідної:
![]()
Доведення.
Застосувавши теорему про похідну
добутку, де
![]() ,
отримаємо
,
отримаємо
![]()
Приклад
а)
![]()
б)
![]()
Теорема
(похідна
частки диференційованих функцій).
Якщо
функції
![]() і
і
![]() мають похідні у всіх точках інтервалу
(a; b), причому
мають похідні у всіх точках інтервалу
(a; b), причому
![]() для будь-якого х є (a; b), то
для будь-якого х є (a; b), то
![]() .
.
Приклад
а)
![]()
б)
![]()
Похідна складеної функції
Нехай
у
= f(u),
де
![]() ,
тобто
,
тобто
![]() .
Функція f
(u)
називається зовнішньою,
а функція
.
Функція f
(u)
називається зовнішньою,
а функція
![]() -
внутрішньою,
або проміжним
аргументом.
-
внутрішньою,
або проміжним
аргументом.
Теорема.
Якщо
у=f(u) та
![]() – диференційовні функції своїх
аргументів, то похідна складної функції
існує і дорівнює
– диференційовні функції своїх
аргументів, то похідна складної функції
існує і дорівнює
![]() .
.
Таким чином, похідна складної функції дорівнює добутку похідної зовнішньої функції за проміжним аргументом на похідну проміжного аргументу за незалежною змінною.
Приклад
1.
Знайдемо похідну функції
![]() .
.
Розв’язання.
Нехай
![]() ,
одержимо
,
одержимо
![]() .
.
Тоді
![]() .
.
Приклад
2.
Знайдемо похідну функції
![]() .
.
Розв’язання.
Нехай
![]() ,
одержимо
,
одержимо
![]() .
.
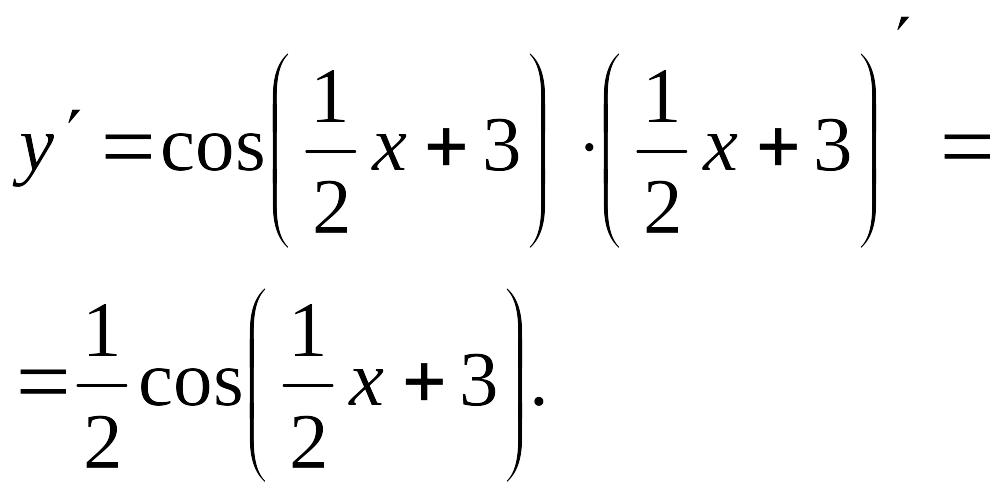
Похідні вищих порядків
Похідна
![]() від функції
від функції
![]() називається похідною
першого порядку
і
являє собою деяку нову функцію. Можливі
випадки, коли ця функція сама має похідну.
Тоді похідна від похідної першого
порядку
називається похідною
першого порядку
і
являє собою деяку нову функцію. Можливі
випадки, коли ця функція сама має похідну.
Тоді похідна від похідної першого
порядку
![]() називається похідною
другого
порядку
від
функції
і позначається
називається похідною
другого
порядку
від
функції
і позначається
![]()
![]() .
.
Похідна
від похідної другого порядку
![]() називається похідною
третього порядку і
позначається
називається похідною
третього порядку і
позначається
![]() ,
,
![]() .
.
Похідна
від похідної (n–1)-го
порядку
![]() називається похідною
n-го порядку
і
позначається
називається похідною
n-го порядку
і
позначається
![]() .
.
Таким
чином,
![]()
Приклад
1.
Нехай
задано
функцію
![]() .
Знайдемо
.
Знайдемо
![]()
Розв’язання.
Маємо:
![]() ,
,
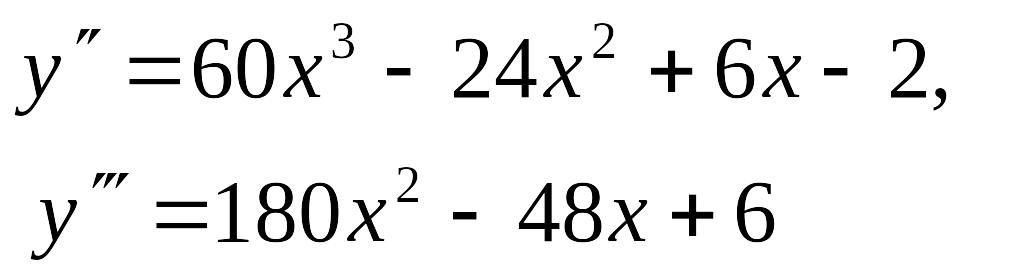
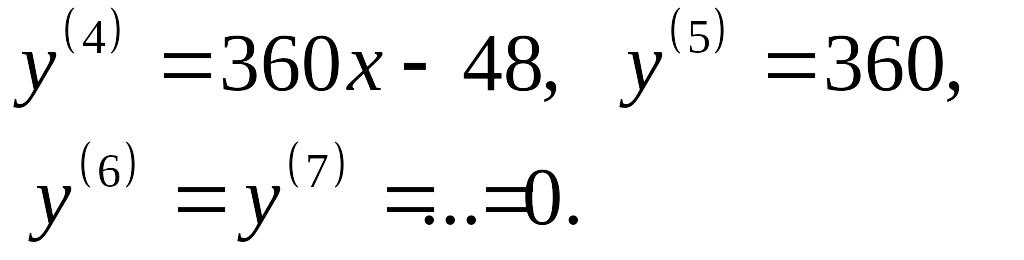
Приклад
2.
Знайдемо
похідну третього порядку для функції
![]() .
.
Розв’язання. Маємо:
![]()
Зростання, спадання функції достатня умова монотонності
Дослідження функції на зростання та спадання ґрунтується на теоремі математичного аналізу.
Теорема
1.
Нехай
функція
![]() неперервна на проміжку
неперервна на проміжку
![]() і
диференційована в інтервалі
і
диференційована в інтервалі
![]() .
Для того, щоб функція була зростаючою
(спадною) на проміжку
,
необхідно і достатньо виконання двох
умов:
.
Для того, щоб функція була зростаючою
(спадною) на проміжку
,
необхідно і достатньо виконання двох
умов:
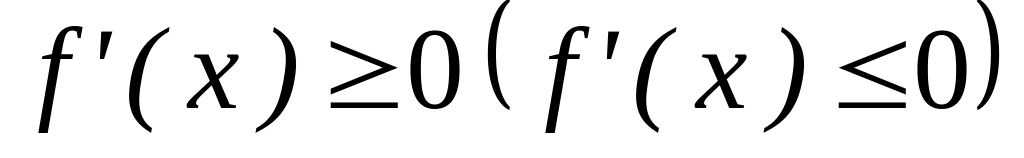 для
всіх
для
всіх
 ;
;рівність
 не повинна виконуватися в жодному
інтервалі, що міститься в
.
не повинна виконуватися в жодному
інтервалі, що міститься в
.
Як наслідок цієї теореми, можна використовувати таку теорему (достатня ознака строгої монотонності):
Теорема
2.
Нехай
функція
неперервна на проміжку
і диференційована в інтервалі
.
Якщо для всіх
![]() виконується
умова
виконується
умова
![]() (
(![]() ),
то функція зростає (спадає) на проміжку
.
),
то функція зростає (спадає) на проміжку
.
Таким чином, щоб дослідити функцію на зростання і спадання, необхідно виконати такі кроки:
Знайти область визначення функції.
Знайти критичні точки, для цього знайти похідну функції і прирівняти її до нуля (а також вказати внутрішні точки області визначення, в яких похідна не існує).
Знайдені точки розбивають область визначення функції на інтервали, необхідно визначити знак похідної функції на кожному інтервалі (взяти довільну точку інтервалу і підставити її у вираз для знаходження похідної).
Скористатись достатніми ознаками зростання і спадання функції: якщо похідна додатна на деякому інтервалі, то функція зростає на цьому інтервалі, якщо ж похідні від’ємна на деякому інтервалі, то функція спадає на цьому інтервалі.
Якщо функція неперервна в кінцевих точках проміжку, їх можна приєднати до проміжків зростання чи спадання.
Розглянемо тепер дослідження функції на зростання чи спадання на конкретних прикладах.
Приклад.
Знайти
проміжки зростання та спадання функції
![]() .
.
Розв’язання.
Функція
визначена і диференційована на множині
R. Знайдемо її похідну
![]() .
.
Нулями
похідної є критичні точки х1=1,
х2=![]() ,
які розбивають область визначення
функції на три інтервали (рис. 1).
,
які розбивають область визначення
функції на три інтервали (рис. 1).
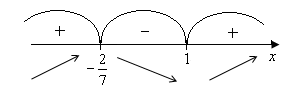
Рис. 1.
Оскільки
похідна задана квадратним тричленом з
додатним коефіцієнтом при х2,
то вона набуває додатних значень поза
коренями, тобто
![]() на інтервалах
на інтервалах
![]() ,
і від’ємних між коренями, тобто
,
і від’ємних між коренями, тобто
![]() на інтервалі
на інтервалі
![]() .
.
Отже,
на інтервалах
функція зростає, а на інтервалі
–
спадає. Запишемо проміжки зростання та
спадання функції з урахуванням
неперервності функції на кінцях проміжку:
функція зростає при
![]() ,
функція спадає при
,
функція спадає при
![]() .
.
