МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ

ТА продовольства УКРАЇНИ

ЛУБЕНСЬКИЙ ФІНАНСОВО-ЕКОНОМІЧНИЙ КОЛЕДЖ ПДАА

Матеріали для самостійного вивчення

з дисципліни «Вища математика»

для студентів 2 курсу

Спеціальності:

5.03050901 “Бухгалтерський облік”

5.03050801 “Фінанси і кредит”

5.03050401 “Економіка підприємства”

5.03050702 “Комерційна діяльність”

Розглянуто і схвалено на засіданні

циклової комісії природничо-математичних дисциплін

Протокол № ___ від «__» _____________ 20__ р.

Голова циклової комісії _______________ Л.І. Крят

Тема 1. Елементи лінійної алгебри

Питання для самостійної підготовки

1. Системи т рівнянь з п невідомими.

2. Ранг матриці.

3. Теорема про сумісність систем рівнянь першого степеня (теорема Кронекера-Капеллі)..

Поняття, терміни та формули, які необхідно знати

Системи лінійних рівнянь, їх класифікація за кількістю розв’язків.

Поняття рангу матриці, його знаходження

Теорема Кронекера – Капеллі.

Системи т рівнянь з п невідомими

Нехай маємо систему лінійних рівнянь з невідомими:

Упорядкований набір чисел називається розв’язком системи, якщо при підстановці їх у кожне рівняння системи отримується правильна рівність.

Розглянемо класифікацію систем лінійних рівнянь залежно від кількості розв’язків:

Нехай А – основна матриця системи (складена з коефіцієнтів при невідомих), А|В – розширена матриця (утворена з основної приєднанням стовпця вільних членів). Застосовуючи метод Гаусса, можна звести розширену матрицю системи до ступінчастого вигляду, що дає можливість визначити ранг (кількість лінійно незалежних рівнянь системи) за кількістю ненульових рядків.

Ранг матриці

Розглянемо матрицю А розміром

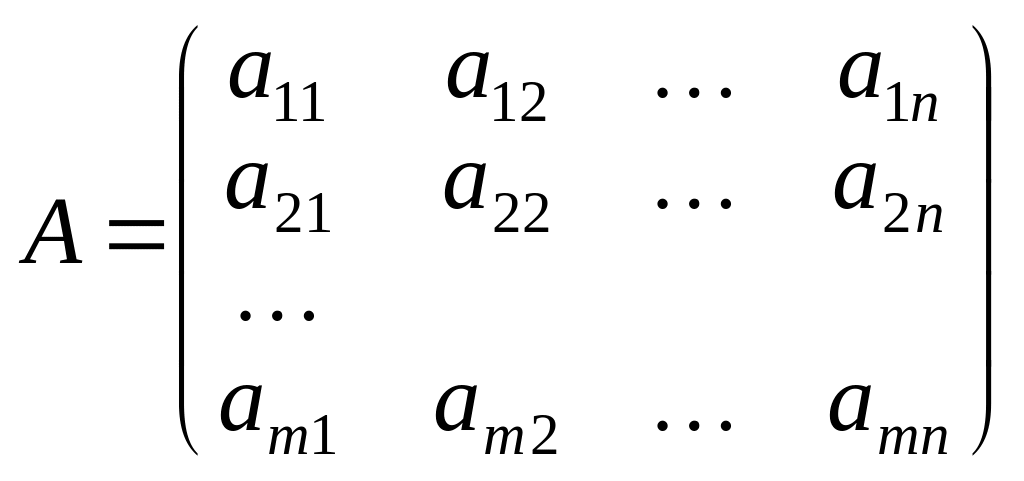
і введемо ще одне важливе поняття.

Рангом матриці А розміром називається найвищий порядок відмінного від нуля мінора, утвореного з елементів цієї матриці. Зрозуміло, що , а найбільший можливий ранг матриці може дорівнювати меншому з чисел m і n.

Розглянемо також поняття обвідного мінора k-го порядку. Це буде такий мінор -го порядку, який повністю містить у собі мінор k-го порядку.

Обчислюючи ранг матриці, потрібно переходити від мінорів менших порядків, відмінних від нуля, до мінорів більших порядків. Якщо вже знайдено відмінний від нуля мінор М k-го порядку, то достатньо обчислити лише мінори -го порядку, що обводять мінор М. Якщо всі вони дорівнюють нулю, то ранг матриці дорівнює k. Якщо серед них знайдеться такий, що відмінний від нуля, то далі для нього будуються обвідні мінори -го порядку і т. д.

Елементарними перетвореннями матриці А називаються такі її перетворення:

1. заміна місцями двох рядків або двох стовпців матриці;

2. множення рядка або стовпця матриці на довільне відмінне від нуля число;

3. додавання елементів одного рядка або стовпця до відповідних елементів іншого рядка або стовпця, попередньо помноженого на деяке число.

Теорема. Елементарні перетворення не змінюють рангу матриці.

Далі матриці, які мають рівні ранги, називатимемо еквівалентними матрицями. Еквівалентні матриці об’єднуватимемо знаком «~» («тильда»).

Знайти ранг матриці А методом обвідних мінорів, якщо

.

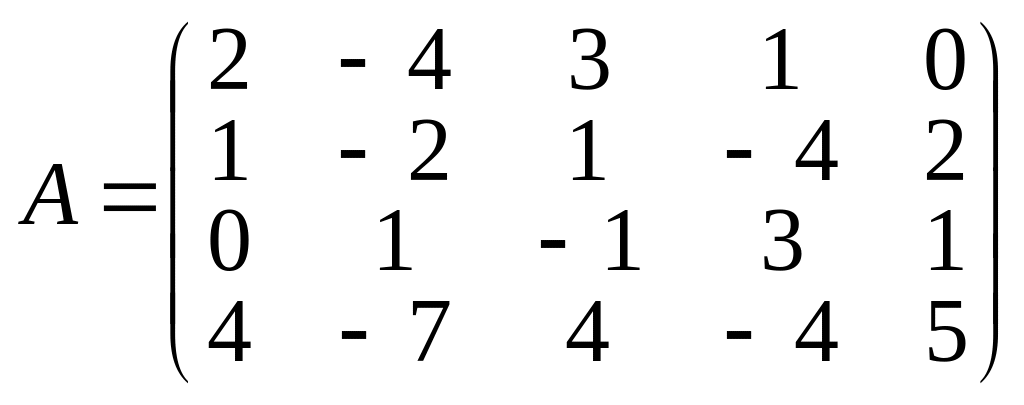Мінор другого порядку, який міститься в лівому верхньому куті цієї матриці, дорівнює нулю: . Проте матриця А має й відмінні від нуля мінори другого порядку, наприклад . Далі запишемо мінор третього порядку, який обводить відмінний від нуля мінор другого порядку:

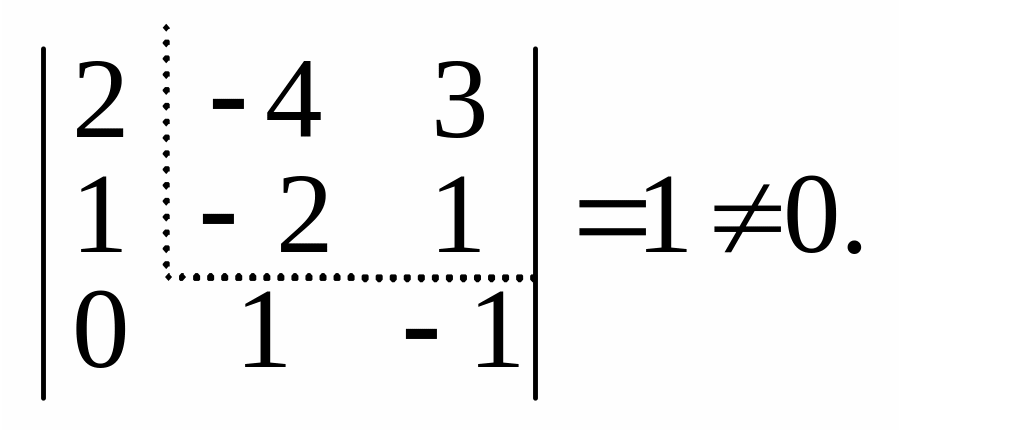
Утворимо тепер обвідні мінори четвертого порядку для мінора третього порядку. Їх існує лише два:

Обидва вони дорівнюють нулю, а це означає, що ранг початкової матриці дорівнює трьом.