Тема 10.

1. Используйте метод синдромного декодирования линейного группового кода (Тема №8, п.1) для контроля над ошибками, если получены слова:

Решение:

Используйте метод синдромного декодирования линейного группового кода (п.6.б) для контроля над ошибками, если получены слова:

комбинация 01 соответствует третьей строке транспонированной проверочной матрицы, что означает, что ошибка произошла во втором информационном разряде.

комбинация 10 соответствует четвертой строке транспонированной проверочной матрицы, что означает, что ошибка произошла во втором информационном разряде.

2. Используйте метод синдромного декодирования линейного группового кода (п.8.4) для контроля над ошибками, если получены слова:

Решение:

Получено слово .

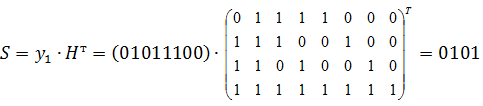
комбинация 0101 соответствует шестой строке транспонированной проверочной матрицы, что означает, что ошибка произошла во втором информационном разряде.

Получено слово .

–

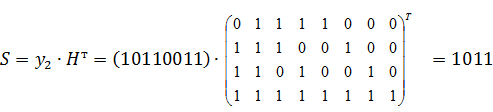комбинация 1011 соответствует четвертой строке транспонированной проверочной матрицы, что означает, что ошибка произошла во втором информационном разряде.

3. Используйте метод синдромного декодирования линейного группового кода (п.6.б) для контроля над ошибками, если получены слова:

Решение:

⇒ комбинация 01 соответствует первой строке транспонированной проверочной матрицы, что означает, что ошибка произошла во втором информационном разряде.

⇒ комбинация 10 соответствует третьей строкам транспонированной проверочной матрицы, что означает, что одиночная ошибка произошла в третьем информационном разряде.

Тема 11. 1. Источник имеет следующие символы алфавита с их частотами появления:

символ	а	б	с	д	е	я
частота	8	6	3	4	5	2

Постройте кодовое дерево Хаффмана. Постройте кодовое дерево Хаффмана.

Решение:

Алгоритм Хаффмана изящно реализует общую идею статистического кодирования с использованием префиксных множеств и работает следующим образом:

1. Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте.

2. Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагаем равной сумме вероятностей составляющих его символов. В конце концов построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него.

3. Прослеживаем путь к каждому листу дерева, помечая направление к каждому узлу (например, направо - 1, налево - 0) . Полученная последовательность дает кодовое слово, соответствующее каждому символу.

Построим кодовое дерево для сообщения со следующим алфавитом:

символ	а	б	с	д	е	я
частота	8	6	3	4	5	2
	а	б	е	д	с	я
	8	6	5	4	3	2
	а	б	е	ся	д
	8	6	5	5	4
	дся	а	б	е
	9	8	6	5
	бе	дся	а
	11	9	8
	адся	бе
	17	11
	адсябе
	28

0

1

1

0

0

1

с

е

1

0

0

1

б

д

1

0

я

а

Запишите код Хаффмана.

буква	код
с	01
д	001
а	0001
е	10
б	110
я	1110

2. Источник имеет следующие символы алфавита с их частотами появления:

символ	а	щ	н	х	з	к	и
частота	8	2	12	1	4	7	6

Постройте кодовое дерево Хаффмана.

Решение:

Алгоритм Хаффмана изящно реализует общую идею статистического кодирования с использованием префиксных множеств и работает следующим образом:

1. Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте.

2. Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагаем равной сумме вероятностей составляющих его символов. В конце концов построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него.

3. Прослеживаем путь к каждому листу дерева, помечая направление к каждому узлу (например, направо - 1, налево - 0) . Полученная последовательность дает кодовое слово, соответствующее каждому символу.

Построим кодовое дерево для сообщения со следующим алфавитом:

символ	а	щ	н	х	з	к	и
частота	8	2	12	1	4	7	6
	н	а	к	и	з	щ	х
	12	8	7	6	4	2	1
	н	а	к	и	з	щх
	12	8	7	6	4	3
	н	а	к	щхз	и
	12	8	7	7	6
	щхзи	н	а	к
	13	12	8	7
	ак	щхзи	н
	15	13	12
	щхзин	ак
	25	15
	щхзинак
	40

0

1

1

0

0

1

щ

н

1

0

0

1

а

х

1

0

0

к

з

и

Запишите код Хаффмана.

буква	код
щ	01
х	001
з	0001
и	0000
н	10
а	110
к	1110

3. Источник имеет следующие символы алфавита с их частотами появления:

символ	а	н	т	я	е	в	к	р	т
частота	7	12	3	2	9	4	5	8	1

Постройте кодовое дерево Хаффмана. Постройте кодовое дерево Хаффмана.

Решение:

Алгоритм Хаффмана изящно реализует общую идею статистического кодирования с использованием префиксных множеств и работает следующим образом:

1. Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте.

2. Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагаем равной сумме вероятностей составляющих его символов. В конце концов построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него.

3. Прослеживаем путь к каждому листу дерева, помечая направление к каждому узлу (например, направо - 1, налево - 0) . Полученная последовательность дает кодовое слово, соответствующее каждому символу.

Построим кодовое дерево для сообщения со следующим алфавитом:

символ	а	н	т	я	е	в	к	р	т
частота	7	12	3	2	9	4	5	8	1
	н	е	р	а	к	в	т	я	т
	12	9	8	7	5	4	3	2	1
	н	е	р	а	к	в	т	ят
	12	9	8	7	5	4	3	3
	н	е	р	тк	ятв	а
	12	9	8	8	7	7
	рятв	тка	н	е
	15	15	12	9
	рятвн	ткае
	27	24
	рятвнткае

0

1

1

0

0

1

н

е

1

0

0

1

а

в

1

0

1

0

т

т

к

я

Запишите код Хаффмана.

буква	код
н	01
в	001
т	0001
я	0000
е	10
а	110
т	1110
к	1111

Тема 12. 1. Записать матричное соотношение расчета апериодической (линейной) дискретной функции взаимной корреляции последовательностей Вычислить коэффициенты корреляции, построить график корреляционной функции.

Решение:

Апериодическая взаимокорреляционная функция для последовательностей и длины N и M определяется как

.

Это выражение можно записать в матричной форме.

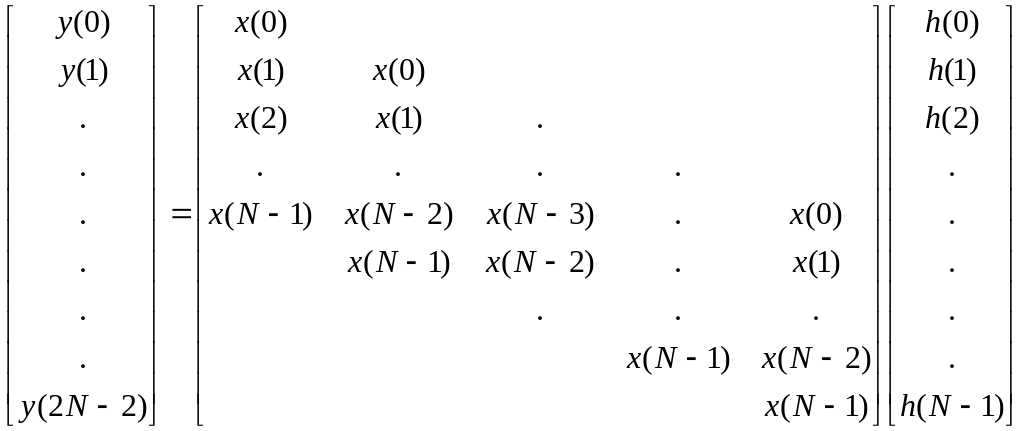
11

10

9

8

7

6

5

4

3

2

1

1 2 3 4 5 6 7 8 9

2. Записать матричное соотношение расчета апериодической (линейной) дискретной функции взаимной корреляции последовательностей Вычислить коэффициенты корреляции, построить график корреляционной функции.

Решение:

Апериодическая взаимокорреляционная функция для последовательностей и длины N и M определяется как

.

Это выражение можно записать в матричной форме.

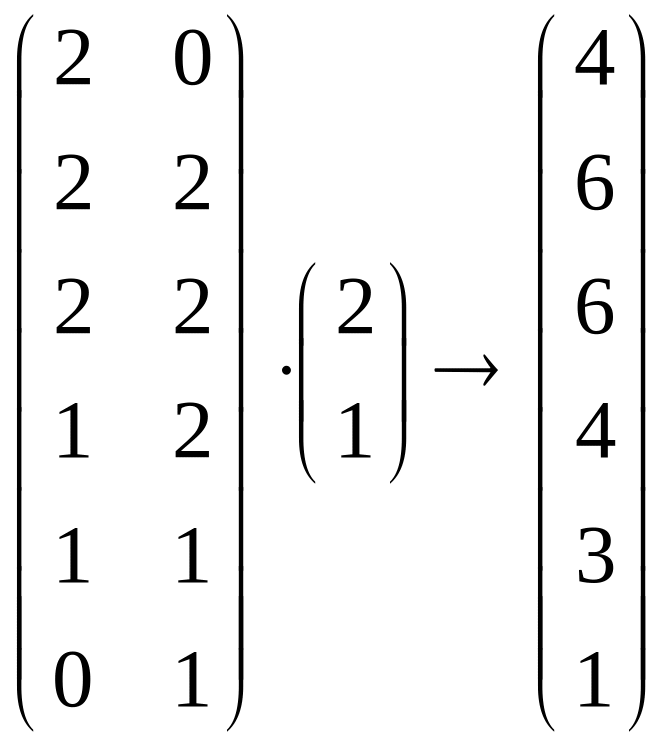
11

10

9

8

7

6

5

4

3

2

1

1 2 3 4 5 6 7 8 9

3. Записать матричное соотношение расчета апериодической (линейной) дискретной функции взаимной корреляции последовательностей

Вычислить коэффициенты корреляции, построить график корреляционной функции.

Решение:

Апериодическая взаимокорреляционная функция для последовательностей и длины N и M определяется как

.

Это выражение можно записать в матричной форме.

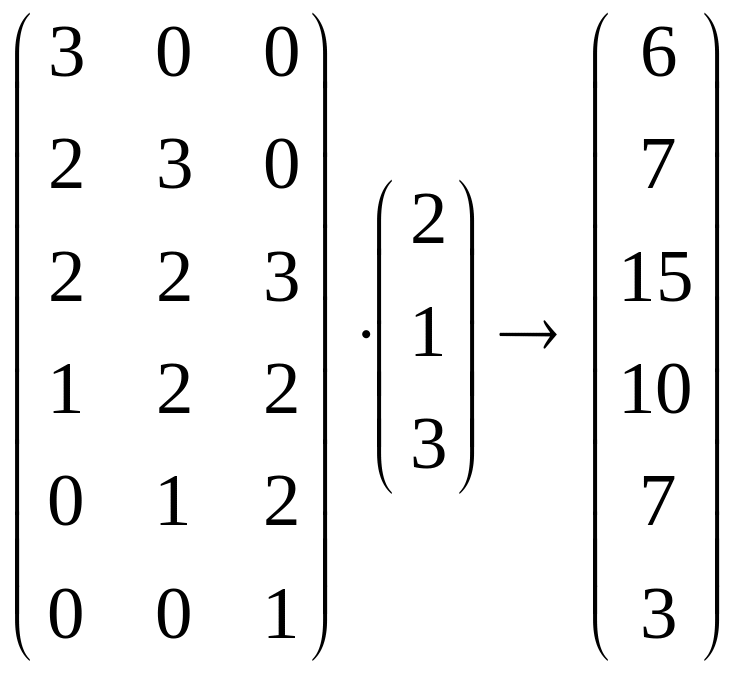
15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

1 2 3 4 5 6 7 8 9