Тема 8.

1. Построить порождающую 𝐺 и проверочную матрицы линейного группового кода с проверкой на четность с параметрами [𝑛; 𝑛 ‒1; 2], 𝑘 = 3.

Решение:

Порождающая матрица:

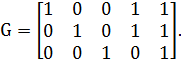
Проверочная матрица:

.

k = 3 – кол-во информационных символов, r = 2 – кол-во проверочных символов в кодовом слове, n = 5 – длина кодового слова.

2. Построить порождающую 𝐺 и проверочную матрицы линейного группового кода с повторением с параметрами [𝑛; 1; 𝑛], 𝑛 = 5.

Решение:

Порождающая матрица состоит из одной строки, так что код с повторением имеет всего два слова: одно содержит только нули, второе – только единицы. Понятно, что кодовое расстояние равно n.

G=(1,1,1,1,1)

Проверочная матрица кода имеет (n-1) строк и n столбцов и указывает, что сумма первого и любого другого символов кодового слова должна равняться 0. Число избыточных символов в коде достигает нижней границы, следовательно, коды нечетной длины с повторением относятся к совершенным.

Длина кодового слова n = 5, кол-во информационных символов k = 1, кодовое расстояние dmin= 5, кол-во проверочных символов r = n – k = 4.

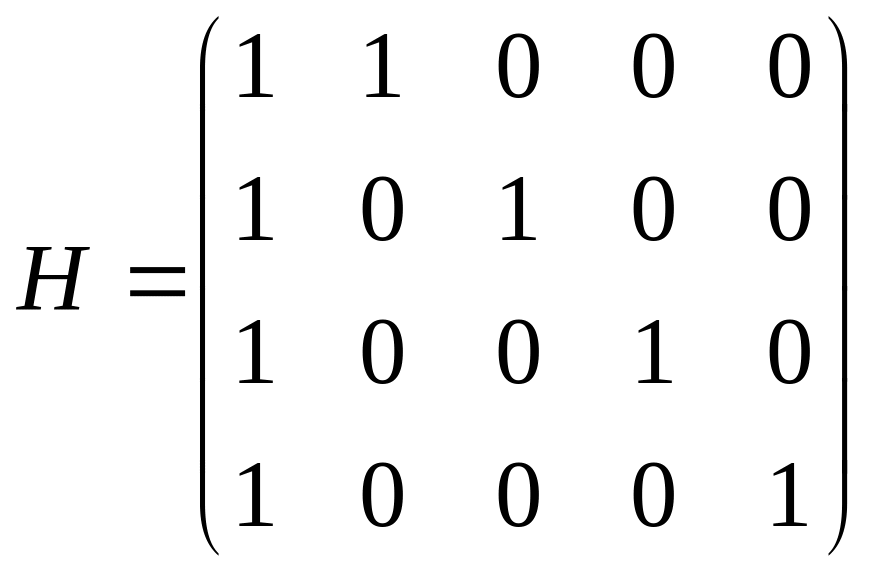
3. Построить порождающую 𝐺 и проверочную матрицы линейного группового кода Хэмминга с параметрами [7; 4; 3].

Решение:

Порождающая матрица линейного группового кода Хэмминга с параметрами [7; 4; 3]:

Для построенного (7, 4)-кода проверочная матрица имеет вид:

4. Построить порождающую 𝐺 и проверочную матрицы линейного группового расширенного кода Хэмминга с параметрами [8; 4; 4].

Решение:

Порождающая матрица кода повторения есть (1,1,1,1,1,1,1,1).

Порождающая матрица расширенного кода Хэмминга с параметрами [8; 4; 4]:

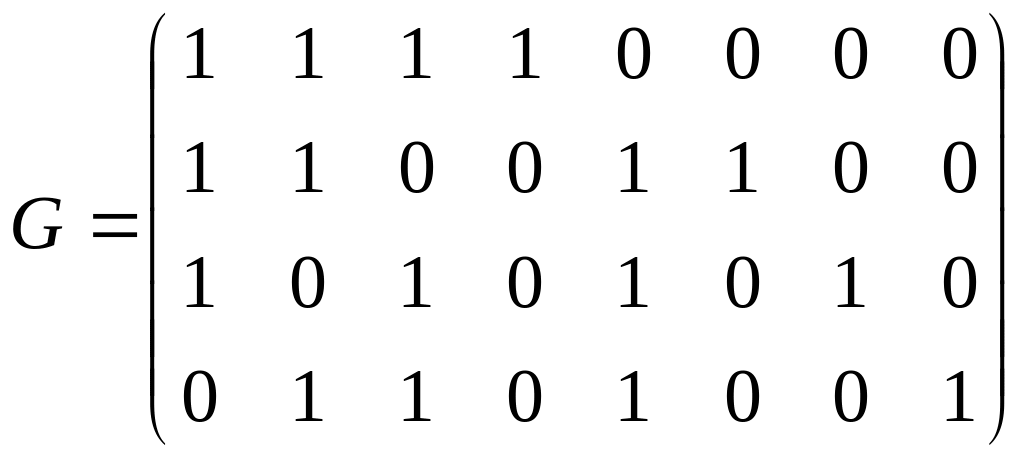
Проверочная матрица:

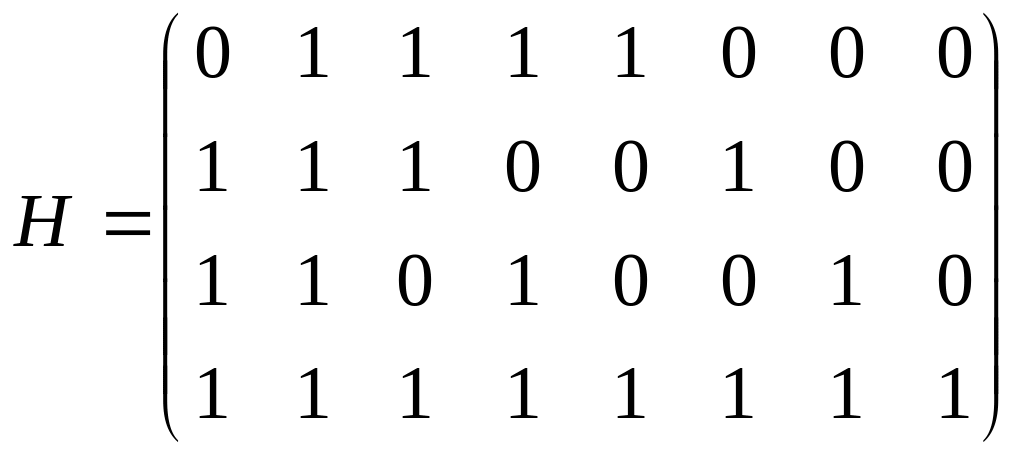
5. Задана порождающая матрица 𝐺 линейного группового кода

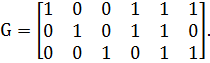
Найти проверочную матрицу кода.

Тема 9.

1. Используйте таблицу смежных классов кода (п.8.1) для контроля над ошибками (обнаружения или исправления ошибок), если получены слова:

Решение:

Таблица смежных классов:

00000	00101	01011	01110	10011	10110	11000	11101
10000	10101	11011	11110	00011	00110	01000	01101
00100	00001	01111	01010	10111	10010	11100	11001
00010	00111	01001	01100	10001	10100	11010	11111

Получено слово . Используя таблицу смежных классов, получим, что кодовое слово принято без ошибки.

Получено слово . Используя таблицу смежных классов, получим, что кодовое слово принято без ошибки.

2. Используйте таблицу смежных классов кода (Тема №8, п.2) для контроля над ошибками (обнаружения или исправления ошибок), если получены слова:

Решение:

Таблица смежных классов:

00000	10110	01101	11011
00001	10111	01100	11010
00010	10100	01111	11001
00100	10010	01001	11111
01000	11110	00101	10011
10000	00110	11101	01011
00011	10101	01110	11000
01010	11100	00111	10001

Процедура исправления ошибок следующая. Принятое кодовое слово анализируют и определяют, в каком столбце таблицы смежных классов оно находится, а затем в качестве исправленного кодового слова берут слово, находящееся в верхней строке. 

3. Используйте таблицу смежных классов кода (п.8.3) для контроля над ошибками (обнаружения или исправления ошибок), если получены слова:

Решение:

Процедура исправления ошибок следующая. Принятое кодовое слово анализируют и определяют, в каком столбце таблицы смежных классов оно находится, а затем в качестве исправленного кодового слова берут слово, находящееся в верхней строке.