Глава 3

ТЕЛЕВИЗИОННЫЕ СИГНАЛЫ, ПЕРЕДАВАЕМЫЕ ПО СПУТНИКОВЫМ КАНАЛАМ

Способы модуляции при передаче телевизионной информации по спутниковым каналам

Чтобы передавать телевизионную информацию со спутника, нужно изменять или амплитуду, или частоту, или фазу несущей электромагнитной волны, то есть модулировать любые (один или два) ее параметры в соответствии с передаваемой информацией. Для этого применяются амплитудная, частотная, фазовая, импульсно-кодовая и другие виды модуляции.

Амплитудная модуляция. Амплитудная модуляция с одной бо­ковой полосой (AM ОБП - DSB), используемая в наземных переда­чах и для передач со спутников была бы наиболее приемлемой, так как здесь относительно экономно используется полоса частот. Од­нако работа с AM крайне невыгодна энергетически, - при этом только 5% мощности используется на передачу информации, а ос­тальные 95% тратятся на передачу бесполезной несущей волны. При работе с AM ОБП энергетические соотношения несколько улучшаются, так как на передачу информации используется около 35% всей излучаемой мощности.

На орбите, как известно, самым трудным и дорогостоящим яв­ляется получение необходимой излучаемой мощности от бортового передатчика спутника. Главное препятствие здесь - это ограничен­ные возможности источника электроэнергии, в качестве которого используются солнечные батареи, отдающие от 1,5 до 10 кВт элек­трической мощности, которая расходуется еще на обеспечение "живучести" систем спутника в целом. В силу этого мощность пере­датчика спутника нельзя сделать как угодно большой, а из-за по­терь на рассеяние при прохождении огромного расстояния между спутником и наземными приемными устройствами, а также из-за потерь в атмосфере Земли, электромагнитная волна со спутника настолько ослабевает, что у земной поверхности ее уровень становится ниже естественного уровня помех и шумов. Эти ослабления велики в диапазоне частот 10,7...2,7 ГГц и использование AM ОБП энергетически невыгодно.

Частотная модуляция. В системах спутникового телевизионно­го вещания при передаче аналоговым способом применяется час­тотная модуляция (ЧМ), то есть при передаче информации изменя­ется частота несущей электромагнитной волны, а амплитуда ее ос­тается постоянной и мощность передатчика при излучении не из­меняется. Она всегда равна пиковой, тогда как при амплитудной модуляции мощность максимальная при излучении немодулированной (бесполезной) несущей волны, а при передаче информации (при модуляции несущей) уменьшается в 3...4 раза. Поэтому, чтобы получить требуемую полезную эквивалентную мощность при пере­даче информации, мощность передатчика при излучении электро­магнитной волны с AM должна быть в четыре раза выше, чем при ЧМ. При частотной модуляции:

□ при передачах на большие расстояния нужна значительно меньшая мощность, что очень важно для бортовых передатчиков спутника;

□ подводимый для передачи сигнал имеет постоянную амплиту­ду, поэтому требования по обеспечению линейности режима рабо­ты выходного каскада выполняются всегда. Более того, примене­ние ЧМ позволяет работать выходному каскаду в режиме ограниче­ния, что повышает его коэффициент полезного действия и, тем са­мым, в целом к.п.д. всего ретранслятора (транспондера);

□ излучаемая передатчиком мощность в процессе передачи ин­формации постоянна, не изменяется во времени, поэтому в местах приема сохраняется стабильный уровень сигнала, что очень важно для ведения приема со спутников;

□ обеспечивается меньшая чувствительность к помехам и шу­мам за счет применения при передачах коррекции как высокочас­тотной, так и низкочастотной (предыскажений) и обратной коррек­ции при приеме;

□ обеспечивается значительный выигрыш по отношению к шу­мам, благодаря применению на приемной стороне частотного де­модулятора с его S-образной передаточной характеристикой и фильтров низших частот.

И еще, частотная модуляция обладает высокой помехоустойчи­востью, так как помехи, возникающие в канале связи, воздействуют в основном на амплитуду сигнала, а не на частоту, что позволяет осуществлять связь при невысоком отношении сигнал/шум.

Как недостаток, следует отметить, что при ЧМ несущей требу­ется довольно широкая частотная полоса, Однако для спутнико­вых каналов при ширине частотной полосы =2 7 (36) МГц и несущих, превышающих 10 ГГц, этот недостаток становится не­существенным.

Частотная модуляция была открыта американским ученым Э.М.Амстронгом в 1936 - 1939 гг. В научных статьях по этому пово­ду писалось, что она имеет крупные недостатки, так как занимает более широкую полосу частот, чем AM. По этой причине ЧМ не на­ходила применения несколько десятилетий. Однако позже было установлено, что при применении частотной коррекции при прие­ме/передаче и занятию широкой полосы частот, при ЧМ можно до­биться значительного снижения шумов и помех. В настоящее вре­мя, благодаря своим преимуществам, ЧМ широко используется:

□ в наземных высококачественных стереосистемах звука;

□ во многих системах спутникового телевизионного вещания.

Фазовая модуляция (ФМ) - это изменение фазы несущей

электромагнитной волны согласно передаваемой информации. При изменении фазы изменяется и частота. Так как частота опре­деляется скоростью изменения фазы во времени, то ЧМ и ФМ очень похожи и отличаются только спектром модулированного сигнала. При модуляции чистым (синусоидальным) сигналом ФМ и ЧМ не различимы. Отличие состоит в индексе модуляции, кото­рый при фазовой модуляции постоянен при любой модулирующей частоте, а при ЧМ, как известно, он принимает разные, мгновен­ные значения, зависящие от частоты модулирующего сигнала. Поэтому все рассмотренные преимущества ЧМ при применении фазовой модуляции сохраняются.

Следует различать часто встречаемые понятия "фазовая моду­ляция" и "фазовая манипуляция". Как видно из предыдущего под модуляцией понимается взаимодействие двух видов колебаний, в результате которого происходит информационное или энергетиче­ское преобразование сигнала. При этом осуществляется любое воздействие на сигнал (линейное, или нелинейное), в том числе и дискретное

Частным случаем модуляции является манипуляция. Понятие "манипуляция" охватывает те случаи воздействия на исходное ко­лебание, при которых фаза получает строго определенное дис­кретное изменение. Как правило, модулятор может всегда выпол­нять функции манипулятора, а манипулятор - не всегда

пряжения, отражающими этот процесс. Он имеет непрерывную ам­плитуду и на оси времени задается множеством точек. Примерами аналоговых сигналов служат сигналы от микрофона, видеосигналы, подводимые к кинескопу телевизора, видеосигналы от телекамеры, сигналы от датчиков температуры воздуха и т.п.

Дискретный сигнал имеет также непрерывный вид, но на оси времени представлен дискретно. Дискретными сигналами считают­ся сигналы от приборов с зарядовой связью, уровни сигнала миниа­тюрного элемента яркости телевизионного изображения и подоб­ные. Дискретные сигналы имеют ограниченное распространение и занимают промежуточное положение между аналоговыми и цифровыми сигналами.

Цифровые сигналы представляются на оси времени в виде дво­ичных импульсных последовательностей, т.е. не имеют непрерыв­ного вида. Цифровыми сигналами оперируют микропроцессорные устройства, запоминающие устройства, регистры, логические эле­менты и т.п.

Преобразование аналогового сигнала в цифровой

В природе и технике в основном все процессы в какой-то момент времени протекают непрерывно и могут быть представлены анало­говыми сигналами. С другой стороны, цифровые сигналы более удобны для обработки и широко распространены в технике.

Любой аналоговый сигнал может быть преобразован в цифро­вой. Это реализуется последовательным выполнением следующих операций: дискретизацией аналогового сигнала -» квантованием (распределением) его дискретных значений по уровням (кодам) -» образованием из кодовых значений цифровых слов—» формирова­нием цифрового кода из совокупности цифровых слов.

Дискретизация. Для преобразования аналогового сигнала в цифровую форму через дискретные промежутки (временные, про­странственные и т.п.) проводят отсчет его значений и получают со­вокупность последовательных дискретных числовых значений, на­пример таких: 0; 0,23; 0,42; 0,57; 0,80; 1,05; 3,0, называемых отсчетами или выборками (рис. 3.1).

Процесс получения последовательных числовых дискретных значений аналогового сигнала через определенные дискретные временные или пространственные промежутки называется дис­кретизацией.

Так как значения отсчетов выражаются цифрами, то процесс часто называют оцифровкой аналогового сигнала

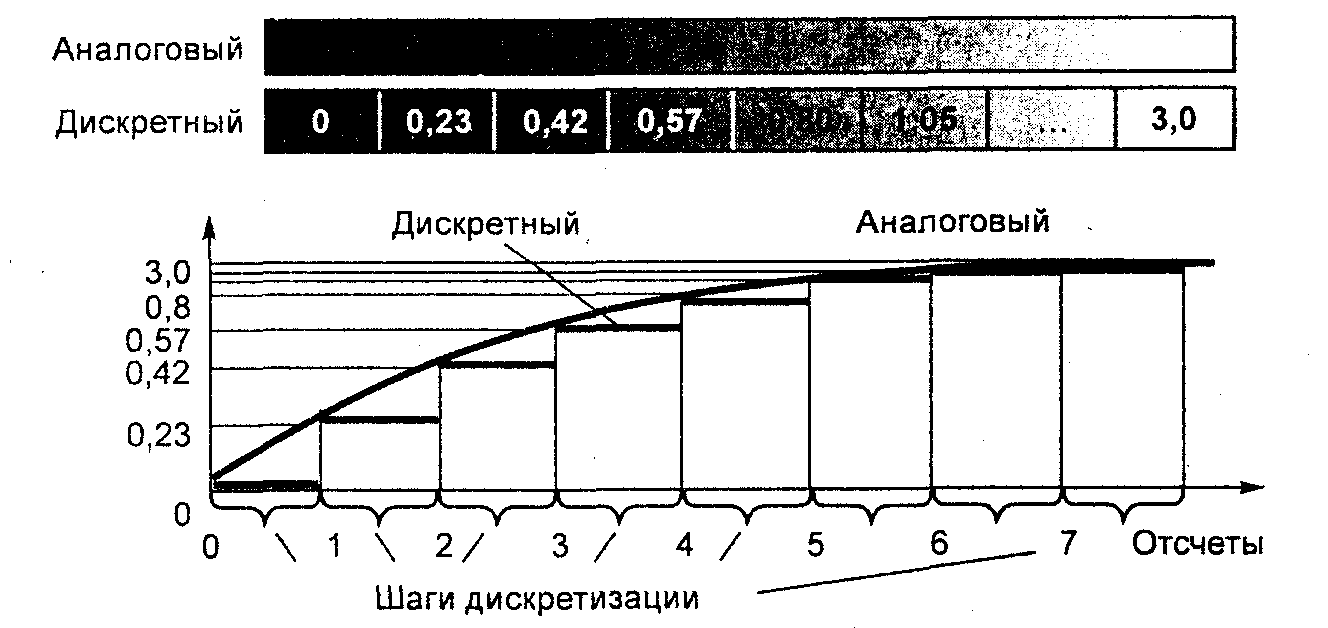
Рис. 3.1. Аналоговый и дискретный сигналы полосы возрастающей яркости и их представление на пространственной оси через отсчеты

Очевидно, чем меньшие промежутки между отсчетами, т.е. чем меньший шаг дискретизации, тем точнее оцифровка аналогового сигнала.

Квантование (от латинского quantum - сколько). Квантование аналогового сигнала широко используется в вычислительной технике и технике связи. Квантуются сигналы, процессы и т.п. по уровням энергии, направлению и скорости движения (вектора дви­жения). Различают амплитудно-пространственное и амплитудно-временное квантование, квантование спектра частот сигнала по амплитуде и т.п. В общем случае процесс квантования понимается как представление аналогового сигнала определенными кодами. Количество кодов отражает количество уровней квантования. Кван­тование аналогового сигнала неразрывно связано с его дискрети­зацией, так как по уровням квантования распределяются числовые значения отсчетов, полученные в процессе дискретизации. При дискретизации аналогового сигнала числовые значения отсчетов могут получаться как целыми, так и дробными. Перевод их на фик­сированные уровни, называемые уровнями квантования, связан с потерей некоторой точности. Реальные числовые значения отсче­тов не всегда совпадают с числовыми значениями уровней кванто­вания, что приводит к заранее допускаемым систематическим ошибкам, так называемым ошибкам квантования.

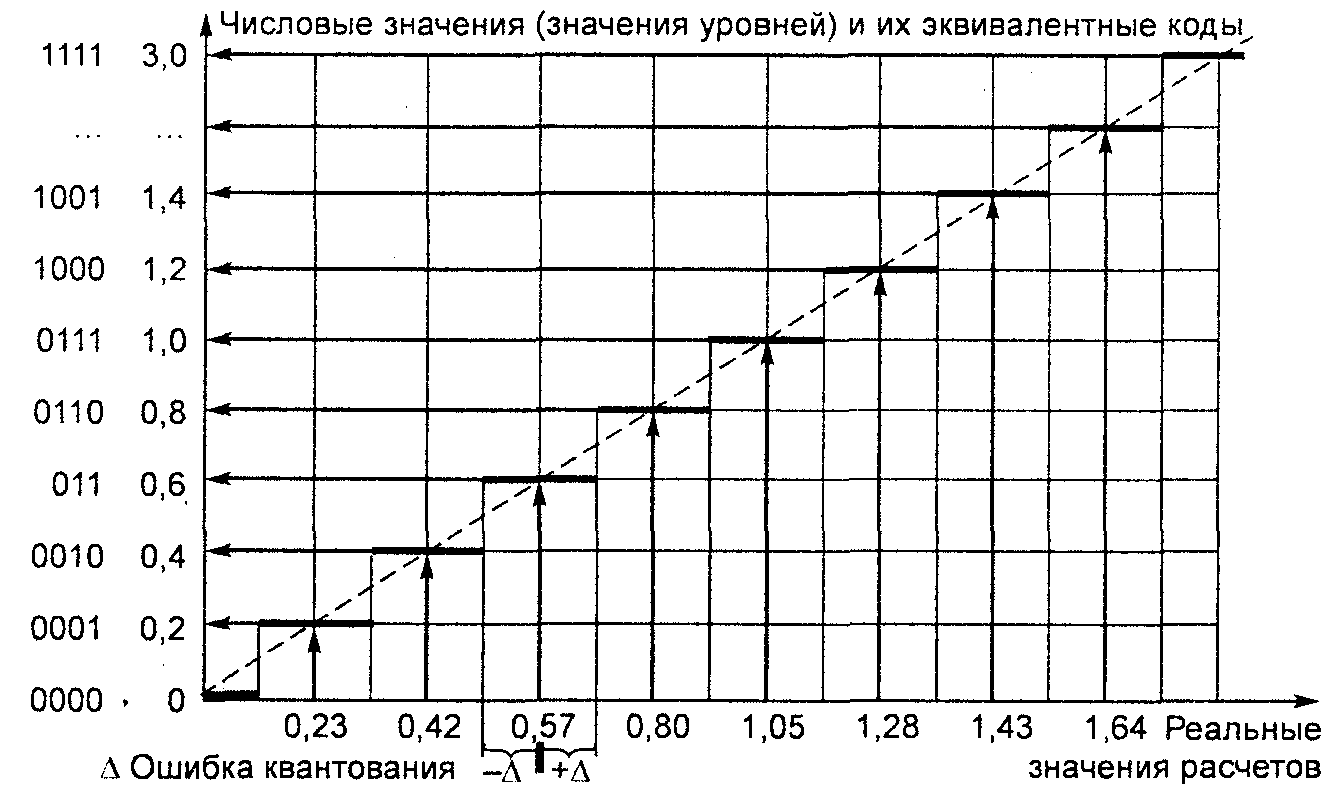
Рис. 3. 2. Процесс квантования аналоговой величины (сигнала)

Например, полученные в результате дискретизации значения отсчетов 0,42 и 0,57 могут представляться при квантовании на уровни, имеющие соответственно значения 0,4 и 0,6. Неточность или ошибка очевидна. Ошибка квантования - это диапазон измене­ния числовых значений отсчета, при котором его кодовая комбина­ция еще не принимает другое значение, а остается постоянной.

Процесс квантования представлен на рис. 3.2. На горизонталь­ной оси отложены числовые, реальные значения отсчетов, которые затем переводятся в числовые значения уровней, и которым при­своены определенные коды. Для уменьшения ошибки квантования передаточная характеристика смещается на - 0,5 цены младшего разряда.

Из рисунка видно, что диапазон ошибки квантования составляет ±0,5 шага дискретизации. Поэтому для получения высокой точности преобразования задают малые (или частые) шаги дискретизации и малые (частые) уровни квантования. Например, если раньше счи­талось достаточным квантовать видеосигнал на 256 уровней, то в настоящее время в студийных передачах для повышения четкости он квантуется на 1024 уровня (или преобразовывается в 1024 кодо­вые комбинации).

Аналоговый сигнал после квантования представляет собой со­вокупность кодов, количество которых соответствует количеству уровней квантования и определяется выражением:

n = 2^N, (3.2)

где N - число уровней (разрядов) кода.

Для передачи код считывается тактовым импульсом и образует определенную последовательность импульсов на временной оси, которая называется цифровым словом (ее еще называют кодовым

словом).

Процесс считывания кодов и формирования кодовых (цифро­вых) слов называется импульсно-кодовой модуляцией (ИКМ).

Двоичный код. Кодовые комбинации уровней (коды) задаются в основном в двоичной системе счисления (системе счисления с основанием 2), т.е. в системе, в которой используются только два равновероятных и возможных состояния - 1 или 0, что в электриче­ских цепях соответствует состоянию включено или выключено. По­этому, электронные логические схемы, работающие по принципу включено/выключено, наилучшим образом подходят для отражения операций, выполняемых в двоичной системе счисления.

Возможность появления одного из двух равновероятных со­стояний, т.е. когда событие может произойти или его, не может быть (1 или 0) носит название единицы информации - бит

Бит - это минимальное количество информации, которое разли­чается и воспринимается цифровой системой. Бит является фун­даментальной единицей в теории информации. Чтобы обеспечить возможность быстрого рационального кодирования таких данных как числа и буквы, используется более крупная единица - байт, со­стоящая из 8 бит (2⁸). Очевидно, что с помощью одного байта мож­но отобразить 256 уровней сигнала яркости или 256 знаков буквен­ного шрифта. Один килобайт это 1024 байта, один мегабайт -1048576 байт.

На практике осуществляют дискретизацию и квантование одно­временно. В большинстве случаев для этого используется аналогово-цифровой преобразователь (АЦП) последовательных прибли­жений, как наиболее популярный, имеющий высокую точность и высокую скорость преобразования. На рис. 3.3 показана его струк­турная схема. В ней в цепь обратной связи включен ЦАП - цифро-аналоговый преобразователь. На входы компаратора подаются два напряжения: обрабатываемого аналогового сигнала и аналоговое линейно изменяющееся напряжение от ЦАП. Компаратор сравнивает величину напряжения цифро-аналогового преобразователя с напря­жением аналогового сигнала, подаваемого на вход компаратора. Если аналоговое напряжение превышает напряжение ЦАП, то на вы­ходе компаратора появляется 1 и схема И разрешает прохождение

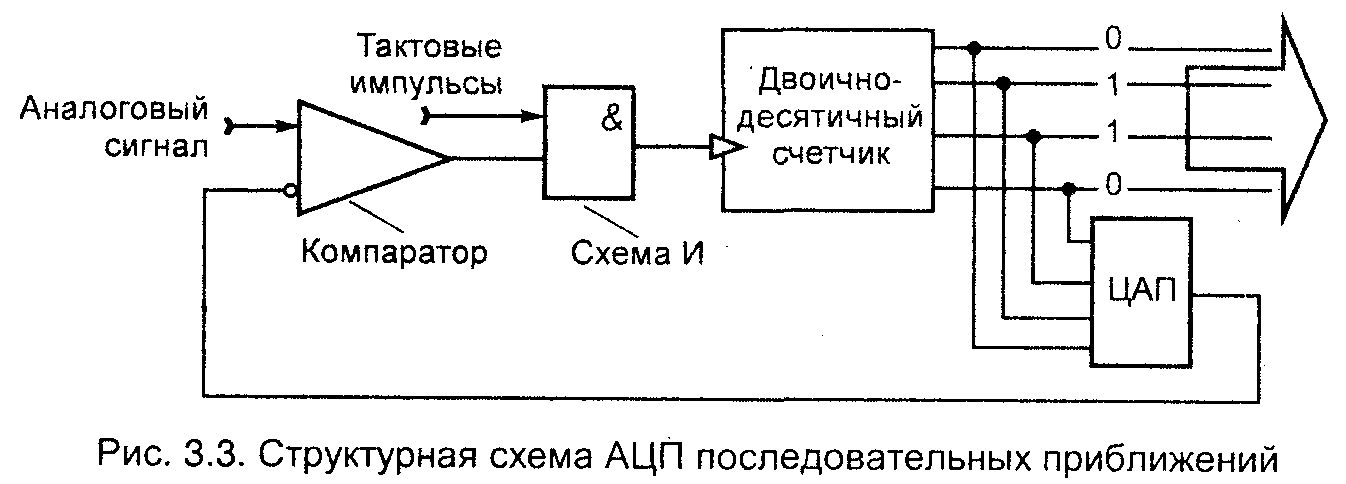
тактовых импульсов на вход двоично-десятичного счетчика. Счет­чик подсчитывает импульсы и постепенно увеличивает двоичное число на выходе.

Счет и увеличение двоичного числа продолжается до тех пор пока напряжение обратной связи (напряжение с ЦАП) не превысит напряжение на входе компаратора. Тогда на выходе компаратора появляется 0 и счет останавливается. На выходе счетчика устанав­ливается выходной код, значение которого соответствует числово­му значению отсчета. Такой АЦП преобразовывает аналоговый сигнал в цифровые слова непосредственно. В этой схеме выделить отдельно дискретизатор невозможно.

Работа дискретизатора на накопительном конденсаторе рас­смотрена на рис. 3.4. В нем для получения многоразрядного кода дискретизацию выполняют, как правило, в два этапа. Вначале при дискретизации производятся отсчеты числовых значений сигнала. Затем полученные значения отсчетов квантуются по уровню. При подаче тактового импульса на вход аналогового ключа он открыва­ется и происходит зарядка конденсатора до амплитудного значения входного сигнала. После окончания тактового импульса входной сигнал отключается от конденсатора, на котором фиксируется ам­плитудное напряжение аналогового сигнала в момент окончания действия тактового импульса. К этому времени и относят его значе­ние отсчета и первый этап заканчивается. Затем отсчет подается на квантователь, который определяет его на соответствующий уро­вень. В промежутках между тактовыми импульсами дискретизатор сохраняет значение предыдущего отсчета. С приходом нового так­тового импульса происходит списывание предыдущего отсчета (происходит разрядка конденсатора) и цикл повторяется с каждым тактом импульса синхронизации, а код считывается тактовым им­пульсом в последовательность импульсов, представляющих циф­ровое (кодовое) слово.

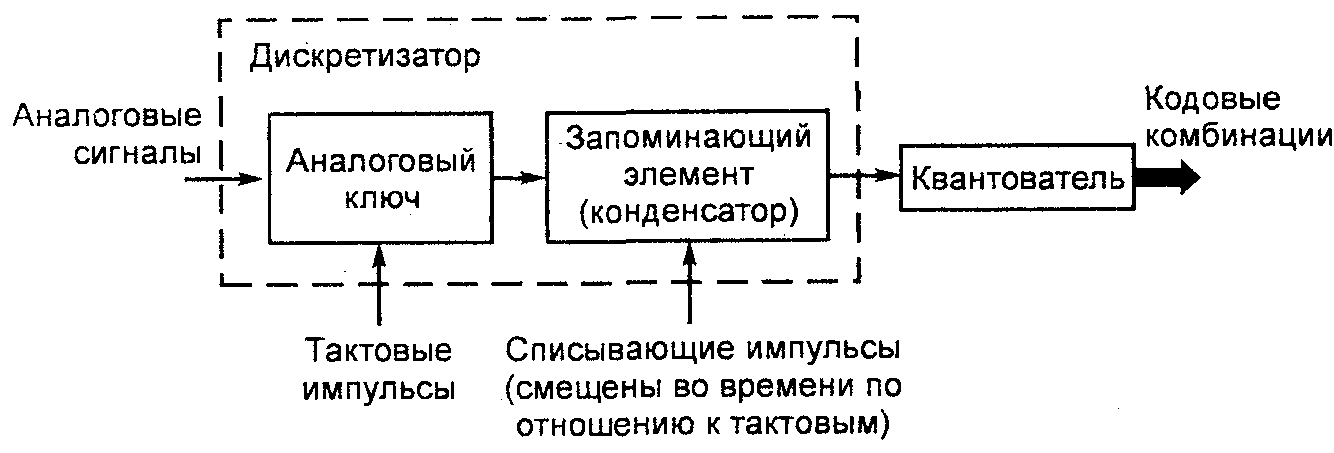
Рис. 3.4. Схема дискретизации аналогового сигнала

Цифровые (кодовые) слова. При считывании тактовым им­пульсом кода, эквивалентного отсчету, получают цифровое слово, которое может передаваться последовательным (рис. 3.5) или па­раллельным (рис. 3.6) способом.

Цифровое слово - это определенная совокупность бит, отра­жающая результат единичного отсчета при дискретизации и представляемая на временной оси определенной последователь­ностью импульсов.

Для передачи цифрового слова последовательным способом в N бит требуется N тактов синхронизации, что снижает скорость передачи информации. Достоинством является то, что для его пе­редачи требуется однопроводная линия и один общий провод. Следует отметить, что цифровая информация по спутниковому ка­налу передается последовательным способом, так же как по одно-проводной линии.

Для получения высокой скорости в компьютерных системах применяется в основном параллельный способ: информация пере­дается битами параллельно, а слова передаются последовательно с каждым тактом синхронизации.

Рис. 3.5. Структура цифрового слова, передаваемого последовательным способом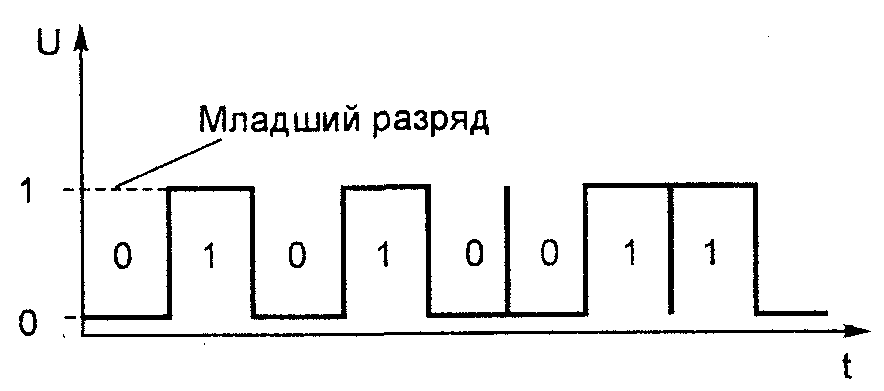

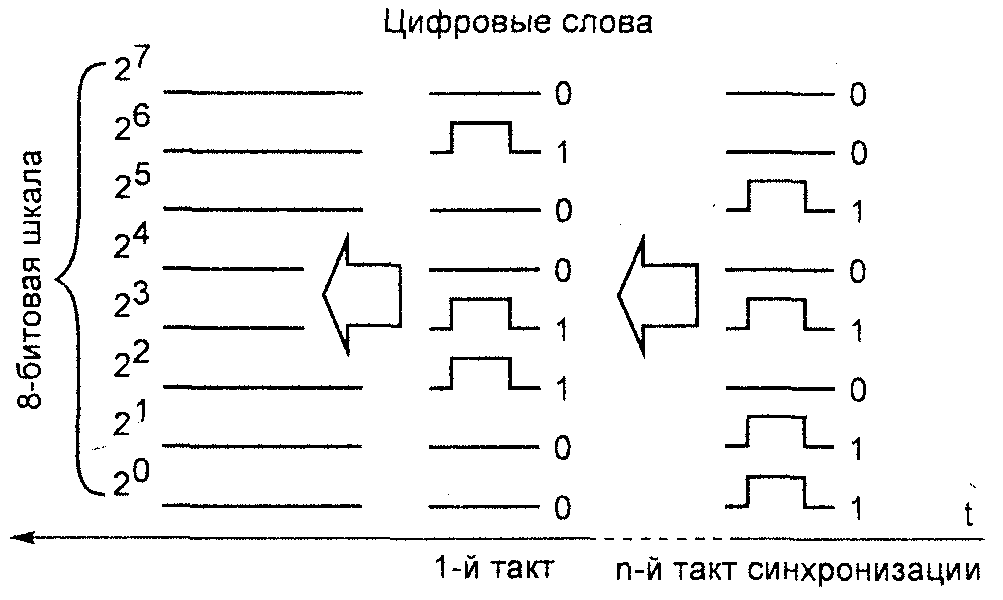
Рис. 3.6. Структура 8-битовых слов передаваемых по параллельной шине-шлейфу при тактах синхронизации

Цифровые слова могут формироваться как 8-и, так и 10-и, 16-и и 32-х битовыми (разрядными) словами. Современные компьютеры оперируют в основном 32 битовыми словами. Передача таких слов параллельным способом осуществляется по 32 каналам (прово­дам) - шине (шлейфу).

Цифровые коды. Одно или множество цифровых слов образу­ют цифровой код, поэтому эти слова называют и кодовыми. Циф­ровой код дает возможность представить аналоговый сигнал в цифровом виде.

Цифровой код - это однозначное отображение суммы множества цифровых слов, сохраняющих неизменными свои основные особенности -структуру, частоту следования и т. п.

Цифровых кодов различных видов используемых для обработки информации множество и каждый имеет свои достоинства и опре­деленное назначение. Это и код Хемминга, и часто встречаемый код Хаффмана, и код Рида-Соломона, сверточные коды и т.п. Они подразделяются на две большие группы: на коды кодирования ис­точника информации и на коды кодирования передаваемых (по каналу связи) данных или просто коды кодирования канала.

Коды кодирования источника информации

Код Хаффмана и некоторые другие коды, например, код LZW, по­зволяют представить обрабатываемую информацию без потерь в цифровом виде меньшим количеством бит. Они направлены на ис­пользование наиболее экономного способа представления в цифро­вом виде аналоговой информации. Эти коды относятся к кодам кодирования источника информации: непосредственно получаемого чи­слового значения отсчета видеосигнала, звукового сигнала и т.п.

Код Хаффмана. При кодировании по Хаффману¹² в первую оче­редь анализируется информация, содержащаяся в сообщении, опре­деляется вероятность появления в нем определенных символов. За­тем все символы располагаются в порядке убывания появления их вероятностей. Символы с большой вероятностью появления кодиру­ются минимальным количеством бит (коротким словом), а символы с малой вероятностью появления - большим количеством бит (длин­ным цифровым словом, если слова меньшей длины уже использова­ны). Основная задача - использовать для передачи сообщения воз­можно меньшее количество бит за счет предоставления наиболее вероятных символов цифровыми словами наименьшей длины, а ме­нее вероятных - цифровыми словами большей длины. Поэтому код Хаффмана представляет собой совокупность цифровых слов пере­менной длины. Например, в текстах на русском языке наиболее час­то встречаются буквы Р, О, И, Е, П. Для увеличения скорости пере­дачи текста (информации) они кодируются очень коротким цифровым словом - одним или двумя битами в 8-битовом слове. Менее встре­чаемые буквы, такие как Ь. Ъ, Ф и т.д. кодируются большим количе­ством бит - более длинным словом. Код Хаффмана обладает свой­ством префексности, т. е. конец одного его слова не является нача­лом следующего цифрового слова, что позволяет обойтись без раз­делителей между словами. Следует отметить, что кодирование по Хаффману не эффективно, если значения элементов в сообщении распределены статистически равномерно, чего при передаче черно-белых изображений практически не бывает.

Метод кодирования по Хаффману предполагает, что в обычных массивах передаваемой информации можно обнаружить много из­быточной или не рационально закодированной информации. Если отдельные знаки, например, буквы, цифры, яркостные элементы изображения, встречаются с различной частотой, тогда они могут быть закодированы очень эффективно по Хаффману.

Коды кодирования данных канала

Полученные при кодировании кодом Хаффмана или другими по­добными кодами сообщения в сжатой экономной цифровой форме очень чувствительны к воздействию помех, которые могут привести к потере целых блоков кодированной информации. Поэтому существуют такие коды, как коды Хемминга, Рида-Соломона, сверточные коды и т.п., позволяющие повысить помехоустойчивость пере­даваемой цифровой информации по каналу приема/передачи, что очень важно. Эти коды относятся к другой большой группе кодов к кодам кодирования данных канала.

Код Хемминга. Кодирование данных канала требует вносить в передаваемые информационные слова некоторое избыточное ко­личество бит, но не случайное, а строго закономерное, теоретиче­ски обоснованное, которое гарантирует требуемую помехоустойчи­вость при передаче. Наиболее просто и эффективно реализуется это способом контроля на четность (или нечетность), при котором обеспечивается постоянная проверка правильности передаваемой информации, и который является основой кода Хемминга.

При рассматриваемом способе контроля цифровое слово содер­жит определенное количество информационных бит, обрабатывае­мых в параллельном виде, а затем для передачи преобразуемых в последовательный вид. Кроме того, формируется информационными битами (возможно и не всеми, а только частью, наиболее важными, в рассматриваемом примере - нечетным количеством) и дополнитель­но вместе с ними передается контрольный бит (паритетный, что зна­чит равнозначный), дополняющий число единиц в передаваемом слове до четного количества. Принцип формирования контрольного бита и схемы контроля на четность показаны на рис. 3.7.

Схема содержит трехвходовый элемент, выполняющий функ­цию ИСКЛЮЧАЮЩЕЕ ИЛИ (не ВКЛЮЧАЮЩЕЕ ИЛИ). Особен­ность этой функции в том, что, если на вход(ы) ее схемы, но не на все, подать нечетное количество логических единиц, то на выходе появится также логическая единица. При четном количе­стве на входах на выходе появится нуль. Состояние на выходе схемы

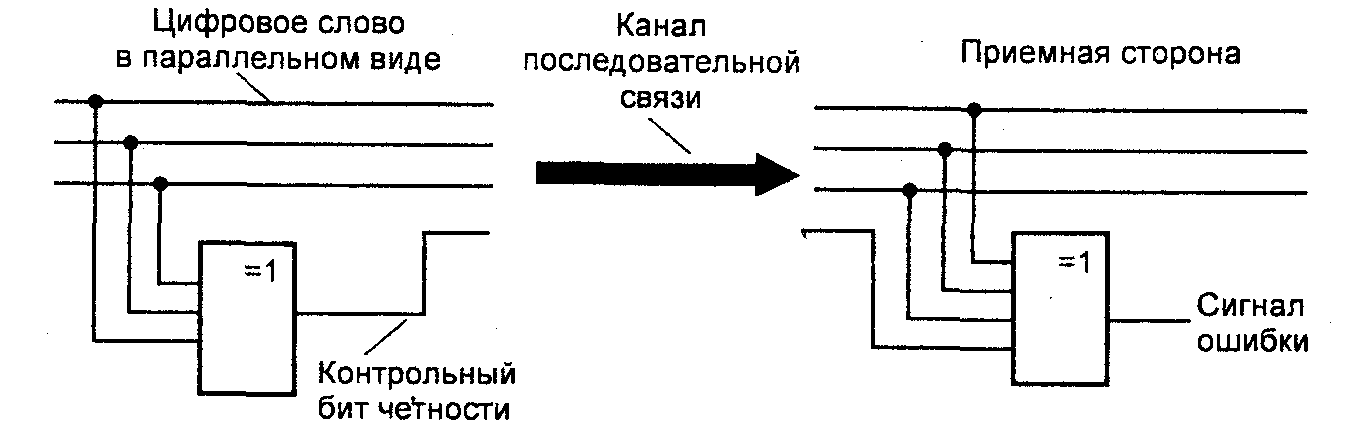
Таблица 3.1

Входы			Выход
Информационные биты			Контрольные биты
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1
Передаваемое цифровое слово при отсутствии ошибки содержит четное число "единиц"

Рис. 3.7. Принцип построения схемы контроля на четность (вариант для трехбитового слова)

Как видно, в каждой строке таблицы, отражающей передаваемое цифровое слово, всегда содержится четное количество единиц: О, 2, 4. Если в передаваемом слове появится ошибка, то оно будет содержать нечетное количество единиц. Это фиксируется детекто­ром ошибок, который находится на приемной стороне и представ­ляет четырехвходовый логический элемент ИСКЛЮЧАЮЩЕЕ ИЛИ. Детектор ошибок обнаруживает нечетное количество принятых единиц и на его выходе появляется единица - сигнал ошибки. Сис­тема с использованием контрольного бита четности обнаруживает ошибку, но не исправляет ее. Исправить ее можно при помощи кода Хемминга, который содержит в цифровом слове несколько допол­нительных бит контроля четности и представляет линейный код с возможностью исправления в слове любой одиночной ошибки. При необходимости исправления нескольких кратных ошибок коды Хемминга обобщаются, что приводит к кодам Боуза-Чоудхури-Хокенгема (БЧХ). Эти коды весьма эффективны и обеспечивают хорошее исправление ошибок, довольно простое аппаратное по­строение (с использованием сдвиговых регистров), кодирование и декодирование. Коды БЧХ при необходимости могут также обоб­щаться и получаются сложные линейные коды Рида-Соломона, дающие возможность исправления блоковых ошибок.