Факторное шкалирование.

Для каждого респондента из выборки можно вычислить значения факторов и, таким образом, заменить исходные п переменных хрх₂,.",х₁₁ на k новых переменных у₁ ,у₂ ,".,yk, причем k зна­чительно меньше п. Эта процедура называется факторным шкалированием. Именно она позво­ляет снизить размерность пространства признаков и сделать статистический анализ более эф­фективным.

Значения факторов, вычисленные с помощью SPSS, обычно лежат в интервале (-4;+4). Отрица­тельные значения фактора размера свидетельстуют о низкой, положительные - о высокой сте­пени его выраженности.

Положительные и отрицательные значения фактора формы противопоставляют две группы респондентов.

Yl

в

А

с

Респондент А - высокие требования к стоимости путевки, умеренные - к глубине и качеству снега;

Респондент В - высокие требования к глубине и качеству снега, умеренные к комфорту (типу подъемника), требований к стоимости путевки нет.

Респондент С - низкие требования к качеству катания, умеренные к стоимости путевки и ка­честву подъемника

Терещенко О .В. Факторный анализ

4

Количественные методы анализа данных в СИ

Пример (домашнее задание). у

____ ----------- ..•...•. ..., .a..a.--.a.'-"'ol..L,Ll.L'-L.l..LY.I. .1.J.IJ""ДlYJ.'-' J. QJ.VJ.
	Первичные з	рактооы	Вращенные Факторы
	Yl	У2	Yl	У2
1. русский язык	0.55	0.43	0.37	0.59
2. английский язык	0.57	0.29	0.43	0.47
3. ИСТОРИЯ	0.39	0.45	0.21	0.56
4. арифметика	0.74	-0.27	0.79	0.00
5. алгебра	0.72	-0.21	0.75	0.05
6. геометрия	0.60	-0.13	0.60	0.08

1. Проинтерпретировать первоначальную факторную структуру.

2. Нарисовать график, на котором изобразить школьников:

А. хорошо успевающего по всем дисциплинам; В. плохо успевающего по всем дисциплинам;

С. хорошо успевающего по гуманитарным дисциплинам, плохо - по математическим; D. хорошо успевающего по математическим дисциплинам, плохо - по гуманитарным.

3. Проинтерпретировать факторную структуру после вращения.

4. Нарисовать график, на котором изобразить школьников:

А. хорошо успевающего по всем дисциплинам; В. плохо успевающего по всем дисциплинам;

С. хорошо успевающего по гуманитарным дисциплинам, плохо - по математическим; D. хорошо успевающего по математическим дисциплинам, плохо - по гуманитарным.

5. Определить, сколько % всей информации об успеваемости сохраняют два фактора.

Выполнение факторного анализа в SPSSWIN

Analyze 1 Data reduction 1 Factor ... / имена анализируемых переменных в окно VariaЫes 1 ОК Функция Descriptives •.. : (Описательные статистики)

univariate descriptives (одномерные описательные статистики) initial solution (первоначальное решение)

correlation matrix: coefficients (матрица корреляций)

Функция Extraction ... : (выделение факторов)

Method: principal components (Метод: главных компонент) Analyze: correlation matrix (Анализировать матрицу корреляций)

Display: unrotated factor solution (Показать невращенное факторное решение) Extract: eigenvalues over ... (Выделить: собственные значения больше ... )

number of factors... (число факторов ... )

Функция Rotation ... : (вращение)

Method: попе (метод: нет- вращение не производится) varimax (ортогональное вращение)

Display: rotated solution (показать вращенное решение)

Функция Scores ••• : (оценки-значения факторов) Save as variaЫes (сохранить как переменные) Method: Regression (метод: регрессия)

Display factor score coefficient matrix (показать матрицу коэффициентов) Функция Options ••• : (параметры)

Missing values: Exclude cases listwise (пропущенные значения: исключить) Exclude cases pairwise (исключить пары)

Replace with mean (заменить средними)

Coefficient display format: (Формат показа коэффициентов)

sorted Ьу size (сортировать по величине)

suppress absolute values less than ... (не показыывать абсолютные зеачения меньше чем ... )

Терещенко О .В. Факторный анализ

5

Количественные методы анализа данных в СИ

Factor Analysis

Communalities

Extraction Method: Principal Component Analysis.

	lnitial	Extraction
LIFEEXPF Average	1.000	.942
female life expectancy
LIFEEXPM Average male	1.000	.933
life expectancy
BABYMORT lnfant		.888
mortality (deaths рег 1000	1.000
live Ьirths)
GDP САР Gross	1.000	.756
dom~tic product / capita
BIRTH_RT Birth rate рег	1.000	.787
1000 people
DEATH_RT Death rate	1.000	.793
рег 1 ООО people
РОР INCR Population	1.000	.795
increase (% per уеаг))

Total Variance Explained

Extraction Method: Principal Component Analysis.

					Extraction Sums of Squared					Rotation Sums of Squared
	lnitial Eiaenvalues					Loadinas						Loadinas
		o/oof					% of						% of
		Varianc	Cumul				Varianc		Cumul				Varianc		Cumul
Comoonent	Total	е	ativeo/o		Total		е		ativeo/o		Total		е		ative %
1	4.073	58.190	58.190		4.073		58.190		58.190		3.744		53.493		53.493
2	1.820	26.005	84.195		1.820		26.005		84.195		2.149		30.702		84.195
3	.451	6.443	90.638
4	.359	5.126	95.764
5	.159	2.274	98.038
6	8.Е-02	1.152	99.190
7	6 Е-02	.810	100.000

Терещенко О .В. Факторный анализ

6

Количественные методы анализа данных в СИ

Component Matri)(l

Extraction Method: Principal Component Analysis. а. 2 components extracted.

	Comoonent
	1	2
LIFEEXPF Average	.952	-.188
female life expectancy
LIFEEXPM Average male	.952	-.163
life expectancy
BABYMORT lnfant	-.849	.408
mortality ( deaths рег 1 ООО
live Ьirths)
GDP САР Gross	.846	-.201
dom;stic product / capita
DEATH_RT Death rate	-.673	-.583
рег 1 ООО people
BIRTH_RT Birth rate рег	7.109Е-02	.884
1000 people
РОР INCR Population	.604	.656
increase (% рег уеаг))

Rotated Component Matrii

Extraction Method: Principal Component Analysis. Rotation Method: Varimax with Kaiser Normalization.

а. Rotation converged in 3 iterations.

	Comronent
	1	2
LIFEEXPF Average	.952	.190
female life expectancy
LIFEEXPM Average male	.942	.213
life expectancy
BABYMORT lnfant		5.246Е-02
mortality (deaths рег 1 ООО	-.941
live Ьirths)
GDP САР Gross	.859	.138
dom;stic product / capita
BIRTH_RT Birth rate рег	-.272	.844
1000 people
РОР INCR Population	.308	.837
increase (% рег уеаг))
DEATH_RT Death rate	-.399	-.796
рег 1 ООО people

Терещенко О .В. Факторный анализ

7

Количественные методы анализа данных в СИ

МНОЖЕСТВЕIПIАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ.

Между двумя переменными существует статистическая связь, если при изменении значения одной пе­еменной меняется распоеделение другой.

Для двух количественных переменных наиболее часто используется модель линейной связи у = Ьх + Ь₀ • Если между двумя переменными существует линейная связь, то при увеличении значения переменной х значение переменной у пропорционально увеличивается (прямая, положительн.ая связь) или

уменьшается (обратная, отрицательнвя связь).

Определить, существует ли связь между переменными и является ли она линейной, прямой или обрат­ной, проще всего по диаграмме рассеяния.

140000---------------~=----1

120000

100000

Линейная связь является полной, если все точки на диаграмме рассеяния лежат на прямой у = Ьх + Ь₀ ; сильной или тесной, если облако точек достаточно прилегает к прямой достаточно близко; слабой, если облако точек по отношению к прямой у = Ьх + Ь₀ широко разбросано.

	80000,							о		о	1
							о			Q
							•	~		в
	60000~			Q			1	о		Q	1		о
						8
						в
е-	400001			в	в	1
"'		1		1
а;					§
сп							§
с:	20000
~
"	о
о
	6	8	10	12	14		16			18			20		22
	Educational Level (years)

Теснота (сила) линейной связи измеряется с помощью коэффициента линейной корреляции Пирсон.а

t(x; -~~;-у) s

r = i=l = ху

I(x; -~rt&i -у}

i=l i=l

где х - среднее арифметическое для переменной х , у - среднее арифметическое для переменной у , s ху - ко вариация переменных х и у ,

s х - среднее квадратическое отклонение для переменной х , s У - среднее квадратическое отклонение для переменной у .

Коэффициент Пирсона обладает следующими свойствами: -I:::;r:::;+I;

r = О , если между переменными нет связи, или если связь не является линейной; r > О, если линейная связь является прямой (положительной);

r < О , если линейная связь является обратной (отрицательной);

при этом чем ближе значение r к + 1 или к -1, тем теснее связь; r = ±1, если связь является полной.

Для сгруппированных переменных коэффициент Пирсона вычисляется по таблице сопряженности.

Терещенко О. В. Множественная линейная регрессия 1

Количественные .методы анализа данных в СИ

Большинство методов многомерной статистики предназначено для анализа структуры связей между не­сколькими переменными. Наиболее полно она описывается матрицей корреляций, в клетках которой указываются значения коэффициентов корреляции для соответствующих переменных. Матрица корре­ляций симметрична относительно главной диагонали, которая полностью состоит из единиц (коэффици­ент корреляции переменной самой с собой равен 1 ).

Correlations

**. Correlation is significant at the 0.01 level (2-tailed).

			Educational	Experience
		Current Salary	Level (vears)	(months)	Female
Current Salary	Pearson Correlation	1.000	.661*'	-.089	-.450*
	Sig. (2-tailed)		.ООО	.053	.ООО
	N	474	474	474	474
Educational Level (years)	Pearson Correlation	.661*'	1.000	-.247*'	-.356*'
	Sig. (2-tailed)	.ООО		.ООО	.ООО
	N	474	474	474	474
Experience (months)	Pearson Correlation	-.089	-.247*'	1.000	-.170*
	Sig. (2-tailed)	.053	.ООО		.ООО
	N	474	474	474	474
Female	Pearson Correlation	-.450*'	-.356*'	-.170*'	1.000
	Sig. (2-tailed)	.ООО	.ООО	.ООО
	N	474	474	474	474

Для коэффициента корреляции r может проверяться гипотеза о статистической значимости. Н₀: r =О

Н, :r-::1;0

Выборочное значение коэффициента является статистически значимым, если по нему можно заключить, что значение коэ<Ьфициента для генеральной совокупности будет отличаться от нvля

Для проверки гипотезы выбранный уровень значимости (а= О.1;0.05;0.01) необходимо сравнить с напечатанным в клетке таблицы значением Sig. (two-tailed).

Если Sig <а, коэффициент корреляции статистически значим (на уровне значимости а); между пере-

менными существует линейная связь.

Если Sig з-а , наличие линейной статистической связи подтвердить не удалось (не исключено, что связь

есть, но она не является линейной).

Различают корреляционные и причинные статистические связи. Корреляционная связь не имеет при­чинной компоненты; для ее измерения достаточно коэффициента корреляции, в который обе перемен­ные входят абсолютно симметрично.

Парная линейная регрессия.

Причинная связь предполагает, что одна из переменных (называемая независимой) измеряет причину, а вторая переменная (называемая зависимой) - следствие. Уравнение у= Ьх + Ь₀ является статистиче­ской моделью причинной линейной связи и называется уравнением регрессии. Независимая переменная обозначена в нем буквой х , зависимая - буквой у . С помощью уравнения регрессии можно предска-

зать, каким будет среднее значение зависимой переменной у при определенном значении независимой переменной х .

Терещенко О. В. Множественная линейная регрессия

2

Количественные методы анализа данных в СИ

Коэффициент Ь называется коэффициентом регрессии и вычисляется по формуле s

b=r_!_,

sx

где s х - среднее квадратическое отклонение для переменной х ,

s У - среднее квадратическое отклонение для переменной у .

Знак коэффициента регрессии совпадает со знаком коэффициента корреляции. Равенство значения ко­эффициента нулю свидетельствует об отсутствии линейной связи.

Коэффициент регрессии показывает, насколько, в среднем, увеличится или уменьшится значение зави­симой переменной у при увеличении значения независимой переменной х на 1.

Коэффициент Ь₀ называется свободным членом уравнения регрессии и вычисляется по формуле Ь₀ = у - Ьх ; во многих задачах он не интерпретируется.

CoefficientSЗ

При повышении уровня образования на 1 год зарплата, в среднем, увеличивается, на $3, 91 О.

Standardi

zed

Unstandardized

Coefficien

--Cnefficients

ts

Model

/

в

-,

Std. Error

Beta

t

Sia.

1

(Constant) (

-18331.2

2821.912

-6.496

~ОМ\

Educational Level (years)

3909.907)

204.547

.661

19.115

.OOOJ

'-

_,

Для параметров регрессии Ь и Ь₀ проверяются гипотезы о статистической значимости по тому же ал­горитму, что и для коэффициента корреляции.

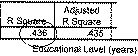
Качество уравнения парной регрессии, его объясняющая способность измеряется коэффициентом де­терминации r²• Коэффициент детерминации показывает, какая доля дисперсии (изменчивости) зави­симой переменной у объясняется влиянием независимой переменной х .

Model Summary

Model

R

Std. Error of the Estimate

.661⁸

$12,833.54

а. Predictors: (Constant),

Интерпретация: 44% всех различий в зарплате объясняется образованием.

Терещенко О. В. Множественная линейная регрессия

3

Количественные методы анализа данных в СИ

Множественная линейная регрессия.

В большинстве задач следствие не может быть объяснено одной единственной причиной; как правило, приходится изучать влияние на него нескольких причин одновременно. Для исследования такой множе­ственной связи используется уравнение множественной линейной регрессии:

k

у= Ь₁х₁ + Ь₂х₂ + ". + bkxk + Ь₀ или, более коротко у= L);x; + Ь₀, где k - количество независимых

i=I

переменных, используемых в анализе:

Coefficient!f

а. Dependent VariaЫe: Current Salary

				Standardi
				zed
		Unstandardized		Coefficien
		Coefficients		ts
Model		в	Std. Error	Beta	t	Sia.
1	(Constant)	-22145.2	3295.029		-6.721	.ООО
	Educational Level (years)	4024.819	210.195	.680	19.148	.ООО
	Experience (months)	12.792	5.770	.079	2.217	.027

По уравнению множественной регрессии можно предсказать, каким будет среднее значение зависимой переменной у при определенных значениях независимых переменных х₁, х₂ ,"., xk.

Например: при образовании 16 лет и опыте работы 24 месяца средняя зарплата составляет у= 4025х16+ 13х 24-22145 = 42567 $

Уравнение множественной регрессии может быть представлено как в нестандартизированном (коэффи­циенты В), так и в стандартизированном виде (коэффициенты Beta). Стандартизированные коэффици­енты показывают величину относительного "вклада" зависимых переменных в изменение независимой переменной.

Например: образование влияет на доход почти в 1 О раз сильнее, чем стаж работы.

Для определения качества модели множественной линейной регрессии используется квадрат коэффици­ента множественной корреляции R ², измеряющий тесноту связи между зависимой переменной у и

набором независимых переменных х₁, х₂ , ••• , х k • R ² является аналогом коэффициента детерминации r ² и интерпретируется как доля изменчивости зависимой переменной у , объясняемая совокупным влия­нием набора независимых переменных х₁ ,х₂ " •• ,xk.

Model Summary

а. Predictors: (Constant), Experience (months), Educational Level (years)

			Adjusted	Std. Error of
Model	R	R Sauare	R Sauare	the Estimate
1	.6658	.442	.440	$12,780.64

Независимые переменные, включенные в одну модель, могут взаимодействовать между собой и опосре­довать влияние друг друга на зависимую переменную. Поэтому лучшей считается модель, в которую в качестве независимых переменных включены все показатели, оказывающие влияние на зависимую пе­ременную.

Терещенко О. В. Множественная линейная регрессия

4

Количественные методы анализа данных в СИ

Использование дихотомических переменных в регрессионном анализе.

Регрессионный анализ изначально предназначался для количественных переменных, однако в последнее время активно развиваются техники, позволяющие включать в регрессионные модели номинальные пе­ременные. Наиболее часто используются дихотомические переменные.

Если дихотомическая переменная используется в качестве зависимой переменной у , уравнение регрессии

будет предсказывать вероятность события, закодированного значением 1.

Если дихотомическая переменная является независимой переменной Х;, коэффициент регрессии для нее по-

казывает, насколько изменится среднее значение у при изменении значения Х; с О на 1.

Coefficients8

а. Dependent VariaЫe: Current Salary

					Standardi
					zed
		Unstandardized		Coefficien
		Coefficients		ts
Model		в	Std. Error		Beta		t		Sig.
1	(Constant)	-8244.827	3796.893				-2.171		.030
	Educational Level (years)	3416.886	221.488		.577		15.427		.ООО
	Experience (months)	1.966	5.766		.012		.341		.733
	FEMALE	-8300.912	1260.475		-.242		-6.586		.ООО

Model Summary

а. Predictors: (Constant), FEMALE, Experience (months), Educational Level (years)

			Adjusted	Std. Error of
Model	R	R Square	R Square	the Estimate
1	.6998	.489	.486	$12,241.88

Вычисление уравнения множественной регрессии.

Уравнение множественной регрессии строится в два этапа.

k

1. Вычисляются коэффициенты стандартизированного уравнения у = L /З;Х; . Для их нахождения

i=I

необходимо решить систему линейных уравнений: /31 + 'i2/32 + 'iз/Зз + ··· + 'ik/Зk = 'iy

r21f31 + /32 + r2з/3з + ··· + r2k/3k = r2y

Гз1/З1 + Гз2/32 + /Зз + ··· + rзk/Зk = rзу

k

2. Коэффициенты нестандартизированного уравнения у = Lh;X; + Ь₀ вычисляются по формулам:

i=I

s -

Ь, = /3; __!_, i = 1,k

S;

k

Ь₀ =у- Lb;X;,

i=I

Терещенко О. В. Множественная линейная регрессия

5

Количественные методы анализа данных в СИ

где х . - среднее арифметическое для переменной Х;, у - среднее арифметическое для переменной у ,

s; - среднее квадратическое отклонение для переменной Х; , s У - среднее квадратическое отклонение для переменной у .

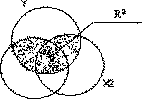
Вычисление коэффициента множественной корреляции.

где ryx₁ - коэффициент корреляции между переменными у и х₁ ,

ryx₂ х, = ~( _ ₂ Jл(² ~'л\ ) - частный коэффициент корреляции между переменными у и х₂ при 1 ryx 1 rx х

2 l 2

устраненном влиянии переменной х₁ ,

при устраненном влиянии переменных х₁ и х₂,

ит.п.

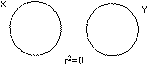
х

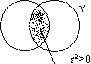
Х1

Х1

SPSS

Построение диаграммы рассеяния:

Graphs 1 Scatter .•. I Simple 1Define1 поместить имена двух переменных в окошки Х Axis и У Axis 1 ОК

Вычисление коэффициента Пирсона:

Analyze 1Correlate1Bivariate1 поместить имена переменных в окно VariaЫes 1 Correlation coefficient: выбрать Pearson 1 Test of significance: выбрать Two-tailed 1 отметить Flag significant correlations 1 ОК

Построение уравнения множественной линейной регрессии:

Analyze 1 Regression 1 Linear ••• 1 поместить имя зависимой переменной в окно Dependent 1 поместить имена независимых переменных в окно lndependent(s) 1 Method: enter 1 ОК

Терещенко О. В. Множественная линейная регрессия 6

Количественные методы анализа данных в СИ