Тема 3. Вариационный анализ

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для глубокого анализа изучаемого процесса или явлений. Необходимо учитывать и разброс или вариацию значений отдельных единиц.

Основные показатели вариации:

- размах вариации;

- среднее линейное отклонение;

- среднеквадратическое отклонение;

- дисперсия;

- коэффициент вариации.

Размах вариации – простейший показатель, равный разности между максимальным и минимальным значениями признака.

Среднее линейное отклонение:

Если каждый вариант в ряду распределения повторяется один раз, то вычисляют среднее линейное отклонение по формуле:

,

где - абсолютные значения отклонений отдельных вариант от их средней величины, n- объем совокупности.

Для вариационного ряда с неравными частотами формула имеет следующий вид.

Среднеквадратическое отклонение:

;

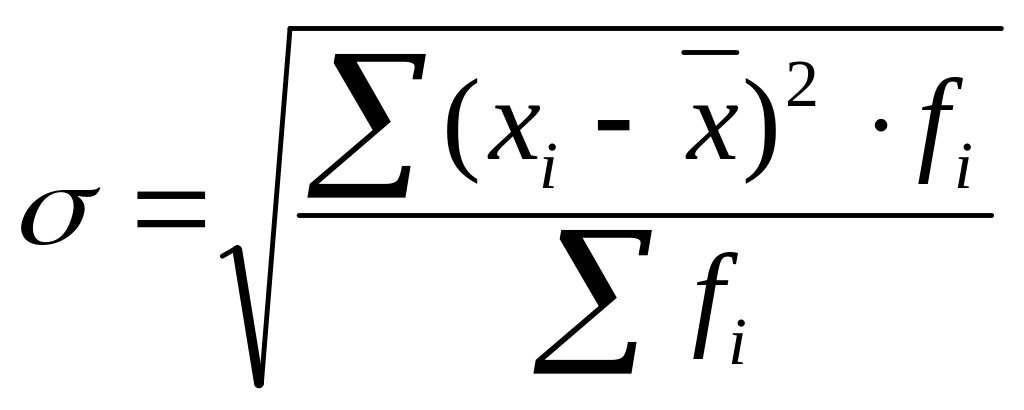
Дисперсия:

;

Коэффициенты вариации:

Формулы коэффициента вариации таковы:

Данный показатель в статистике называется линейным коэффициентом вариации.

Данный показатель называется коэффициентом вариации.

Решение типовых задач

Пример 3.1.

Распределение автомобилей по величине суточного пробега.

Суточный пробег, км	105-120	120-135	135-150	150-165	165-180	180-195	195-210	210-225	225-240
Число автомобилей	25	43	112	77	41	20	25	15	9

Расчет средней величины признака в интервальном вариационном ряду осуществляется по формуле средней арифметической взвешенной.

Для удобства расчетов вычислений построим расчетную таблицу.

Суточный пробег, км	Число автомобилей, fi	Середина интервала, xi	xi* fi	Накопленные частоты, S
105-120	25	112,5	2812,5	25
120-135	43	127,5	5482,5	68
135-150	112	142,5	159605	180
150-165	77	157,5	12127,5	257
165-180	41	172,5	7072,5	298
180-195	20	187,5	3750	318
195-210	25	202,5	5062,5	343
210-225	15	212,5	3187,5	358
225-240	9	232,5	2092,5	367
			57547,5

Средний суточный пробег равен 57547,5/367 = 156,8 км.

В среднем пробег одного автомобиля в сутки составляет 156,8 км.

Мода в данном вариационном ряду распределения будет равна:

Мо = 135 + 15 * (112-43)/((112-43)+(112-77)) = 144,9 км.

Наиболее часто встречающаяся величина суточного пробега составляет 144,9 км.

Для расчета медианы необходимо определить медианный интервал. В нашем случае это будет интервал, в котором находится автомобиль, порядковый номер которого равен (367+1)/2= 184. Для определения медианного интервала рассчитаем накопленные частоты. В первом интервале находятся 25 автомобилей, в двух первых 68, в трех – 180. Автомобиль с порядковым номером 184 попадает в четвертый интервал от 150 до 165 км. Этот интервал и является медианным.

Ме = 150+15 *(½*367 – 180)/77 = 150,7 км.

Следовательно, половина автомобилей автопарка имеет суточный пробег меньше чем 150,7 км, а половина – больше чем 150,7 км.

Для определения среднего линейного отклонения, среднеквадратического отклонения и дисперсии составим расчетную таблицу.

Суточный пробег, км	Число автомобилей, fi	Середина интервала, xi	| |	| |*fi	( )²*fi
105-120	25	112,5	44,3	1107,5	49062,25
120-135	43	127,5	29,3	1259,9	36915,07
135-150	112	142,5	14,3	1601,6	22902,88
150-165	77	157,5	0,7	53,9	37,73
165-180	41	172,5	15,7	643,7	10106,09
180-195	20	187,5	30,7	614	18849,8
195-210	25	202,5	45,7	1142,5	52212,25
210-225	15	212,5	55,7	835,5	46537,35
225-240	9	232,5	75,7	681,3	51574,41
итого	367			7939,9	288197,8

Среднее линейное отклонение:

= 7939,9:367 = 21,6 км.

Среднеквадратической отклонение:

= = 28,0 км

Дисперсия

= 288197,8/367 = 785,3.

Коэффициент вариации

V= 28,0:156,8*100%=17,8%.

Данный показатель свидетельствует об однородности рассматриваемой совокупности.

Задачи

Задача 3.1.

Распределение числа слов в телеграмме в двух почтовых отделениях характеризуется следующими данными:

Количество слов в телеграмме	Почтовое отделение (число телеграмм)
	А	Б
13	20	17
14	22	24
15	37	46
16	26	22
17	20	20
18	15	12
20	10	9
итого	150	150

Определите для каждого почтового отделения:

1. среднее число слов в телеграмме;

2. среднее линейное отклонение;

3. линейный коэффициент вариации;

4. сравните вариацию числа слов в телеграмме.

Задача 3.2.

Распределение длины пробега автофургона торговой фирмы характеризуется следующими данными:

Длина пробега за один рейс, км	30-40	40-50	50-60	60-70	70-80	80 и свыше	итого
Число рейсов за 1 месяц	20	25	14	18	8	5	90

Определите:

1. среднюю длину пробега за один рейс;

2. среднее квадратическое отклонение;

3. коэффициент вариации.

Оцените количественную однородность совокупности.

Задача 3.3.

Распределение численности безработных по возрастным группам в N-м регионе за 2006-2008 гг. характеризуется следующими данными.

Возраст безработных, лет	В % к общей численности безработных
	2006	2008
До 20	7,9	8,6
20-24	18,3	17,7
25-29	13,3	12,4
30-34	12,0	12,0
35-39	14,7	13,0
40-44	13,0	13,8
45-49	10,5	10,7
50-54	5,4	6,7
55-59	3,1	2,6
60-72	1,8	2,5
Итого	100,0	100,0

Определите:

1. для каждого года средний возраст безработного;

2. среднее квадратическое отклонение;

3. коэффициент вариации.

Сравните вариацию возраста безработных за два года.

Задача 3.4.

Распределение населения в двух регионах по величине среднедушевого дохода характеризуется данными, представленными в таблице.

Среднедушевой доход в среднем за месяц, тыс.руб. на 1 чел.	Число жителей, в % к итогу
	Регион А	Регион Б
До 2,0	5,8	5,6
2,0- 4,0	9,7	5,3
4,0- 6,0	13,0	16,1
6,0 – 8,0	19,1	35,2
8,0 – 10,0	22,2	15,5
10,0 -12,0	19,2	14,7
12,0 – 14,0	8,5	4,2
Свыше 14,0	2,5	3,4

1. Рассчитайте средний, модальный и медианный среднедушевой доход.

2. Определите размер и интенсивность вариации доходов населения. Оцените степень однородности распределения населения по величине среднедушевого дохода.

Задача 3.5.

В течение месяца предприятие выпустило четыре партии изделия А. В таблице приведены результаты контроля качества изделий.

Номер партии	1	2	3	4
Число изделий в партии	1000	1200	1500	1000
Число изделий, не отвечающих ТУ	60	72	90	30

Определите:

1. процент брака в каждой партии и в среднем по всем партиям;

2. дисперсию и среднеквадратической отклонение доли брака в целом по четырем партиям;

3. коэффициент вариации доли брака.

Можно ли считать средний процент брака типичным уровнем брака выпускаемой продукции?

Задача 3.6.

Имеется распределение предприятий по объему произведенной продукции.

Группы предприятий по объему продукции, млн.руб.	Число предприятий по управлениям
До 3	3	4	10	5
3-6	5	8	7	9
6-9	9	7	4	15
9-12	4	5	3	17
12-15	2	3	3	10
15 и более	1	2	1	6
Итого	24	29	28	62

Рассчитайте все показатели вариации.