Математические модели объектов и их классификация
В машинной графике получили наибольшее распространение четыре основных математических типа описания моделей объектов:
1. Поверхностями;
2. Сплошными телами;
3. В виде «проволочной сетки»;
4. Точечные.
поверхностные
ячеечные
Рисунок 4 – Классификация моделей, описывающих геометрию объектов.
Первый подход представляет объект в виде тонких поверхностей, под которыми находится пустое пространство, не заполненное материалом объекта. (Эллипсоид - пустое яйцо). Поверхности первого, второго порядков, бикубические.
Поверхности первого порядка.
В системе координат XYZ объект может быть описан поверхностями первого порядка образующих серию многоугольников или треугольников. Внутри многоугольника и треугольника поверхность считается плоской, которая описывается функциями вида:
F1(XYZ) = AX+BY+CZ+D=0
Плоскости ограничены ломанными линиями, которые называют ребрами. Каждое ребро является общим для смежного многоугольника или треугольника. Таким образом, составленная функция, описывающая поверхность, обладает непрерывностью, а производная имеет разрывы в листах стыка участков плоскостей.
Например, поверхность, состоящая из плоских треугольников.
Уравнение плоскости определяют на основании координат трех точек T1(x1 y1 z1), T2(x2 y2 z2), T3(x3 y3 z3), не лежащих на одной прямой
= 0.
Поверхности второго порядка.
Функция вида:
в зависимости от выбора коэффициентов можно описывать поверхности эллипсоида, гиперболоида, конуса, параболоида, цилиндра или двух плоскостей.
С помощью бикубических поверхностей можно описать гладкую поверхность производной формы. Обычно этими функциями описывают смежные участки криволинейной поверхности, добивать гладкости в местах стыка в результате координатного совпадения смежных угловых точек и совпадения первых производных.
Участок такой поверхности может быть представлен параметрически.
X = X(s, t), Y = Y(s, t), Z = Z(s, t),
где
s,
t
– параметры, изменяющиеся в некотором
фиксированном диапазоне, обычно t
[0,1],
s
[0,1].
X(s,
t) = S
;
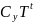Y(s, t) = S
;
Z(s, t) = S
.
Например, матрица 4x4
,
где
,
…,
-
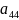постоянные коэффициенты в пределах
данной поверхности; вектор стока S
=
;
вектор строка T
=
.
При описании криволинейных поверхностей из бикубических участков определяются коэффициенты матриц Cx, Cy, Cz внутри каждого участка где, координаты общих узловых точек, задаются касательные вектора в этих точках или систему управляющих точек. Также моделирование может выполняется на основе неоднородных рациональных В-сплайнов (Non-Uniform Rational B-Spline – NURBS поверхности).
Бикубический участок может быть представлен, например, в виде форм (многочлен) Эрмита, Безье, B – сплайнов.
Бикубические поверхности в форме Безье имеют вид:
где
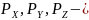матрицы 4 x
4 соответственно координат X,
Y,
Z
для 16-ти управляющих точек.
Например, для
где
-
координаты четырех угловых точек, а четыре тройки остальных точек с индексами 21, 22, 12, 13, 23, 24, 43, 33, 34, 42, 32, 31 являются концами касательных векторов, как показано на рисунке:
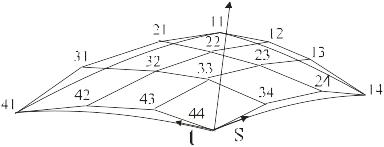
Рис. – Размещение угловых и управляющих точек в бикубическом участке.
Таким образом, геометрия бикубического куска определяется положением 16-ти управляющих точек.
Для гладкого перехода от одного бикубического куска в другой необходимо пространственные совпадения четырех смежных управляющих точек и отсутствие изломов в стыке соприкасающихся кусков.
2. Описание объектов сплошными телами. Они могут быть разделены на три класса:
ячеечные;
моделируемые сплошными геометрическими конструктивами;
представление объекта границами.
Ячеечный методы:
Ограниченный участок производства, объект, считается разбитым на большое число дискретных кубических ячеек (мелкие кубики). Моделирующая система хранит информацию о принадлежности им непринадлежности каждого куба телу объекта. Структура данных представляется трехмерной матрицей, в которой каждый элемент соответствует пространственной ячейке. Метод прост, но требует большой объем памяти для записи объекта с высоким разрешением.
Моделирование сплошными геометрическими конструктивами:
Его еще называют «твердотельное моделирование». Этот метод представляют сложные объекты составляющими из простых объемных примитивов. Примитивы - кубы, цилиндры, конусы, эллипсоиды, и др. фигуры. Над примитивами выполняются «Булевы» (логические) операции для конструирования объекта. Алгоритм конструирования следует например: «взяв шар», вычесть из него цилиндрический примитив; «перенести результат в первую точку пространства»
Представление обьекта границами:
При таком подходе в памяти компьютера сохраняются все элементы, которые создают границы объекта. Такими элементами являются поверхности, края поверхностей и указатели пересечений поверхностей. Одновременно хранят топологическую информацию, которая показывает, как элементы связаны друг с другом.
3.Описание объекта типа проволочной сетки заключается в представлении поверхности серией пресекающихся линий, принадлежащих поверхности объекта.
Поточные описания объекта.
Этот метод применяется при трассировании лучей от объекта к экрану. Объект состоит не из поверхностей, а из множества точек. Основная идея метода заключается в получении изображения каждой точки, описывающий объект. Примером может служить объект сложной сцены, вся информация о которой представлена одной или несколькими стереопарами-фотоизображения. Подобные проблемы могут иметь место при восстановлении форм различных объектов, например, космических.
С использованием методов фотограмметрии по стереоизображению определяются пространственные координаты множества k точек, принадлежащих поверхности объекта.
T
=
Частота точек на объекте должна быть такая, чтобы любые две соседние точки проецировались в два соседних рецептора на экране. Т.е. необходимо рассчитывать расстояние между точками на объекте с учетом масштаба изображения и его разрешения (размером пикселя).