30. Общая характеристика идеальных моделей химических реакторов (допущения об идеальности, характер изменения параметров в зависимости от объема реактора и от времени).

31. Модель реактора идеального смешения периодического действия (рис-п), работающего в изотермическом режиме. Вывод характеристического уравнения.

В РИС-П все реагенты вводят до начала реакции, а все продукты выводят из него только по окончании процесса. В ходе реакционного цикла никаких веществ в реактор не вводят и из него не выводят, так что общая масса реакционной смеси в реакторе остается постоянной, изменяется лишь ее состав. При составлении математического описания принимают, что реакционная смесь однородна по объему аппарата и ее состав зависит только от времени пребывания в периодическом реакторе.

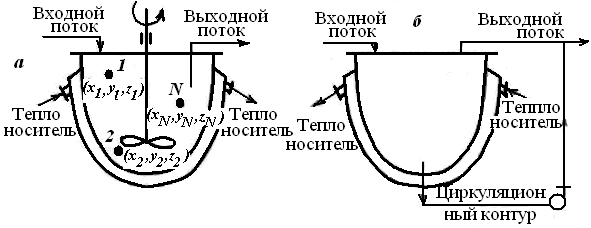
Скорость накопления веществ в реакторе:

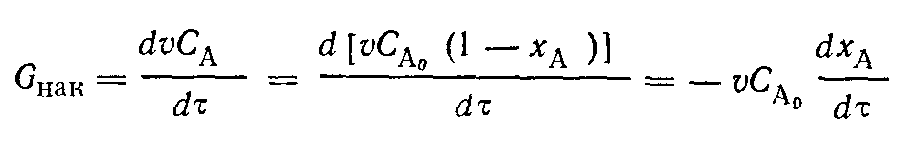
Количество исходного реагента А, вступающего в реакцию в единицу времени:

Уравнение материального баланса:

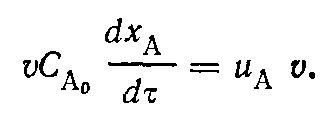
После разделения переменных:

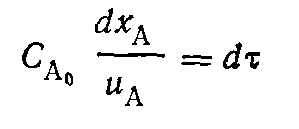
и интегрирования получаем:

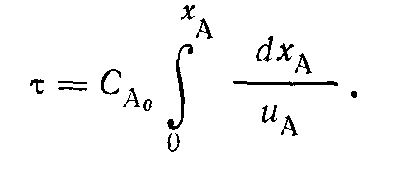
32. Модель реактора идеального смешения непрерывного действия (рис-н), работающего в изотермическом режиме. Вывод характеристического уравнения.

Если необходимо обеспечить получение большого количества продукта одинакового качества, химический процесс предпочитают проводить в непрерывно действующих реакторах с установившимся режимом.

Приход вещества равен

Убыль (расход) составляет

Количество исходного вещества, вступившего в реакцию,

Материальный баланс реактора будет

откуда

33. Модель реактора идеального вытеснения (рив), работающего в изотермическом режиме. Вывод характеристического уравнения.

Реактор идеального вытеснения представляет собой длинный канал, через который реакционная смесь движется в поршневом режиме. Каждый элемент потока, условно выделенный двумя плоскостями, перпендикулярными оси канала, движется через него как твердый поршень, вытесняя предыдущие элементы потока и не перемешиваясь ни с предыдущими, ни со следующими за ним элементами.

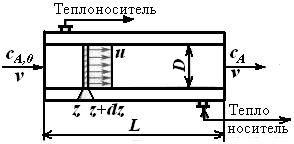
Если рассматривать процесс, протекающий в элементарном объеме реактора dυ за время dτ, то приход реагента в этот объем, может быть представлен как

34. Модель каскада проточных реакторов идеального смешения (рис-к), работающего в изотермическом режиме.

В единичном реакторе Полного смешения, вследствие того, что концентрации реагентов мгновенно снижаются до конечной величины, скорость реакций при больших степенях превращения невелика и потому для достижения высоких степеней превращения требуются реакторы большого объема. Более целесообразна уста­новка ряда последовательно соединенных реакторов полного сме­шения— каскада реакторов. В каскаде реакторов со­став реакционной смеси изменяется при переходе из одного аппа­рата в другой. При этом в каждой ступени каскада, как это характерно для реакторов полного смешения, параметры про­цесса постоянны по всему объему. Для определения числа теоре­тических ступеней каскада используют большей частью алгебраи­ческий и графический методы.

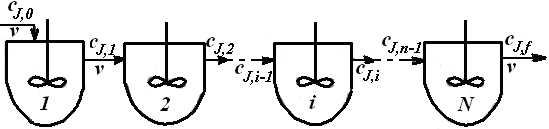
35. Графо-аналитический расчёт каскада проточных реакторов идеального смешения (РИС-К).

↑↑↑ смотри выше ↑↑↑

36. Аналитический метод расчета РИС-К.

↑↑↑ смотри выше ↑↑↑

37. Модель каскада проточных реакторов идеального вытеснения (РИВ-К).

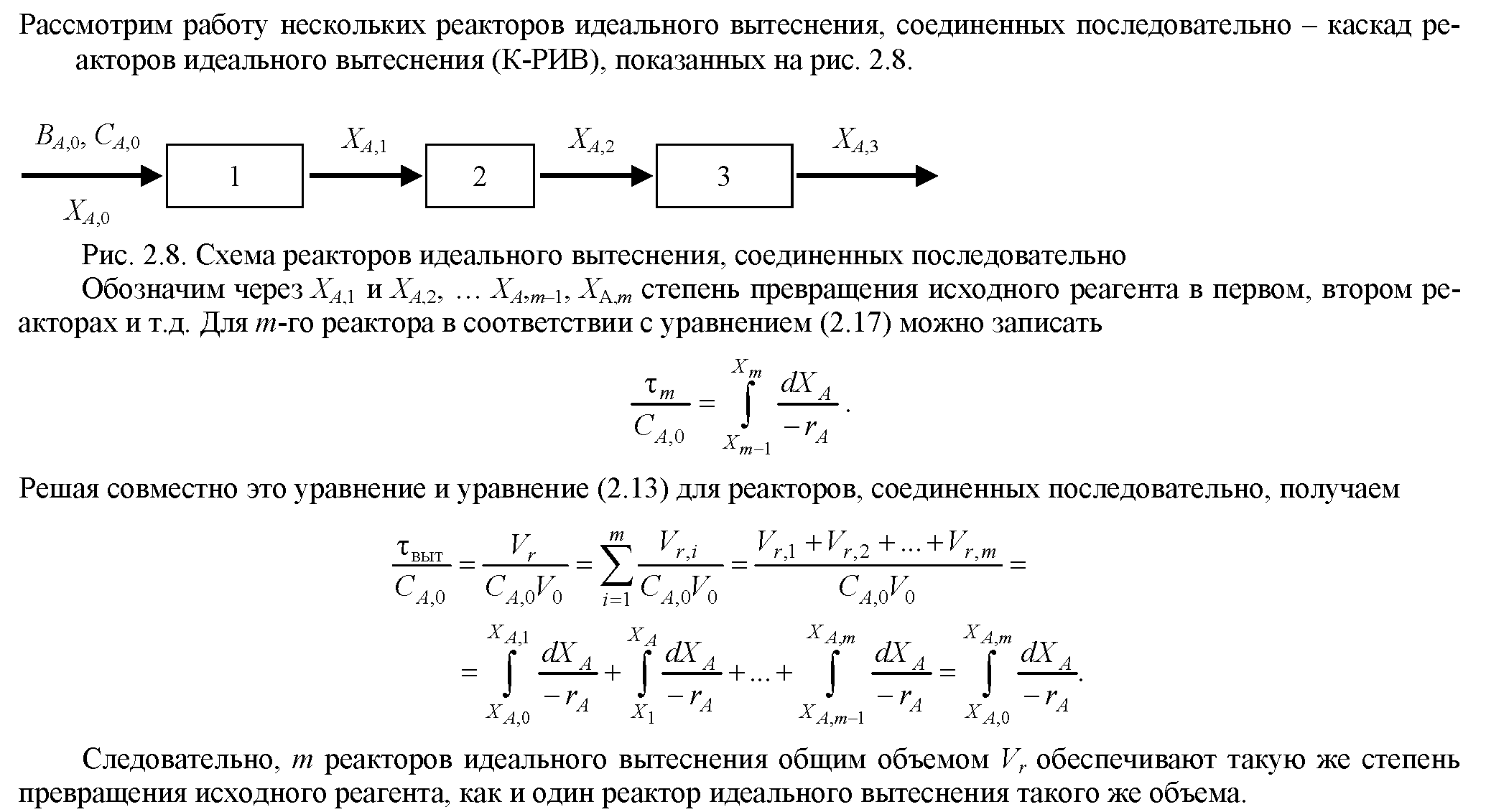
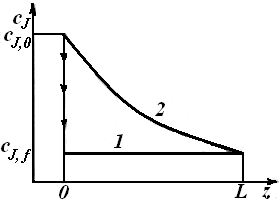
38. Сравнение эффективности работы изотермических химических реакторов, описываемых различными моделями, по объему и интенсивности работы.

При одинаковых условиях проведения одной и той же реакции для достижения равной глубины превращения среднее время пребывания реагентов в проточном реакторе идеального смешения больше, чем в реакторе идеального вытеснения. Этот факт легко может быть объяснен характером распределения концентрации реагентов по объему указанных реакторов. Если в проточном реакторе идеального смешения концентрации во всех точках равны конечной концентрации (линия 1), то в реакторе идеального вытеснения в двух соседних точках на оси реактора концентрации реагентов уже отличаются (линия 2).

Для проточного реактора идеального смешения при заданной глубине превращения (концентрации исходного реагента А в выходном потоке с_А,f или соответствующей степени превращения х_А,f) среднее время пребывания τ можно определить как произведение двух постоянных величин:

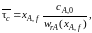
т. е. геометрически представить в виде прямоугольника с соответствующими сторонами.

Для стационарного реактора идеального вытеснения

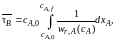
т. е. величина _B как определенный интеграл выражается геометрически площадью криволинейной трапеции.

Площади криволинейных трапеций, соответствующие _B, меньше площадей прямоугольников, соответствующих _С, причем разница тем больше, чем больше достигаемая в реакторе степень превращения исходного реагента. Следовательно, при равном объемном расходе для достижения одинаковых результатов реактор идеального вытеснения должен иметь меньший объем, чем проточный реактор идеального смешения. Интенсивность реактора идеального вытеснения будет выше. Объяснить это можно более высокой скоростью реакции в реакторе вытеснения вследствие более высокой концентрации реагентов.