Метод а.В. Пилягина.

Автор предложил методику определения коэффициентов M_γ, M_q, M_c в формуле (7) СНиП для двухслойного основания со слабым подстилающим слоем. Используется расчетная схема незаглубленного гибкого фундамента. Для анализа напряженно-деформированного состояния грунтового массива используется МКЭ в упругой постановке. Значения напряжений от действия равномерно распределенной нагрузки Р = 0,1 МПа на глубине, равной одной четверти ширины подошвы фундамента, подставляют в условие предельного равновесия В.В. Соколовского.

Максимальная глубина развития областей пластической деформации может быть определена из минимизации функции

Где , , - компоненты напряженного состояния,

Φ - угол внутреннего трения

Коэффициенты M_γ, M_q, M_c подсчитываются по формулам:

?

Где - значение функции из формулы.

Решение л. Прандтля.

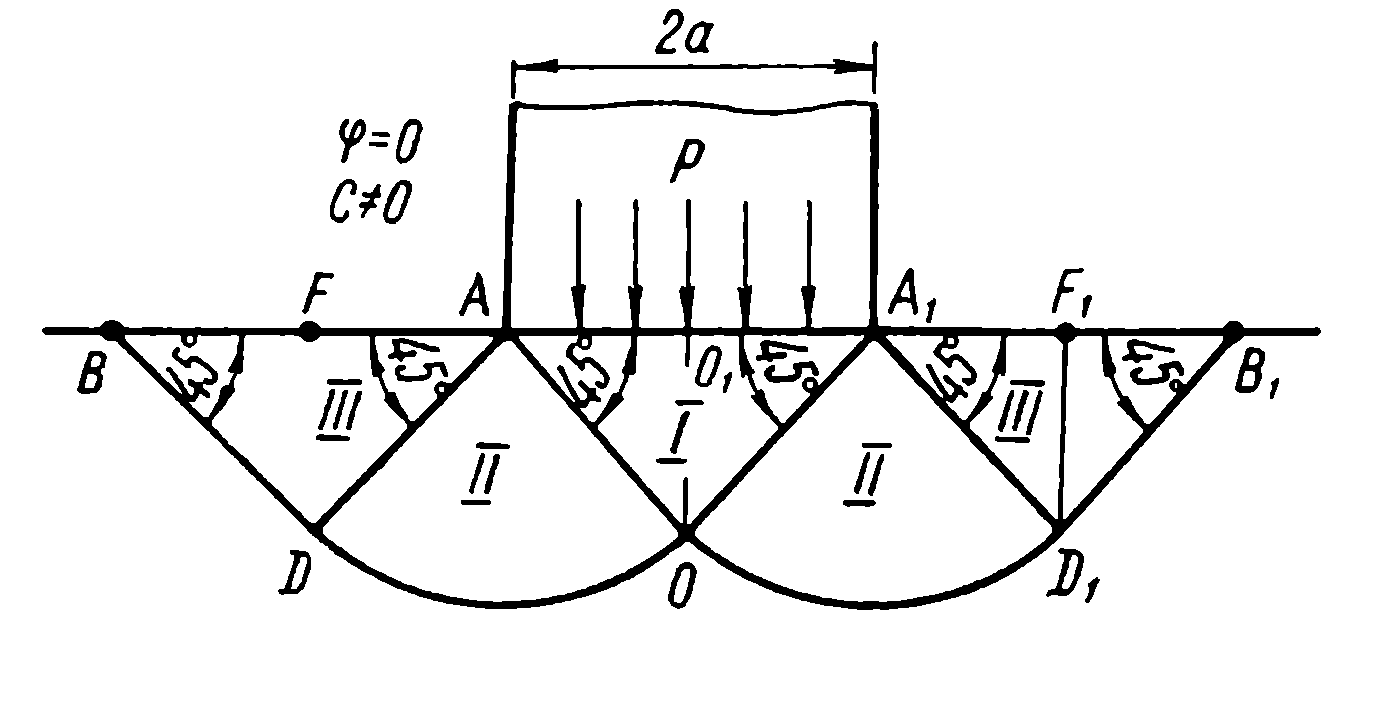
Впервые задача об определении критической нагрузки на основание для условий плоской задачи была рассмотрена Л. Прандтлем. Расчетная схема, предложенная им, до сих пор является основой для большинства исследований в этой области.

По Прандтлю, при приложении к фундаменту нагрузки под его подошвой формируется область (ядро) из уплотненного грунта, которая имеет форму равнобедренного треугольника. Она тесно связана с фундаментом и перемещается совместно с ним, разжимая окружающий грунт в стороны. При достижении критической нагрузки расположенный по обе стороны от ядра грунт теряет свою устойчивость, переходит в пластическое состояние, в результате чего происходит боковой выпор грунта по поверхности скольжения

К настоящему моменту времени решение задачи Прандтля получено для двух частных случаев: невесомого идеально связного грунта и невесомого сыпучесвязного основания

В первом случае конечная формула для плоской задачи имеет вид

,

где с – сцепление грунта.

Если глубина заложения фундамента отлична от нуля, в формулу входит давление от боковой пригрузки.

,

Где - боковая пригрузка

Для грунта с значение предельной нагрузки можно определить по формуле Прандтля-Рейснера, которая также позволяет учесть заглубление фундамента.

Формулу Прандтля-Рейснера часто представляют в следующем виде

Где , - коэффициенты несущей способности Прандтля-Рейснера

,

Недостатки этого метода вполне очевидны:

1) не учитывается собственный вес грунта;

2) значение критической нагрузки не зависит от ширины фундамента

Метод к. Терцаги

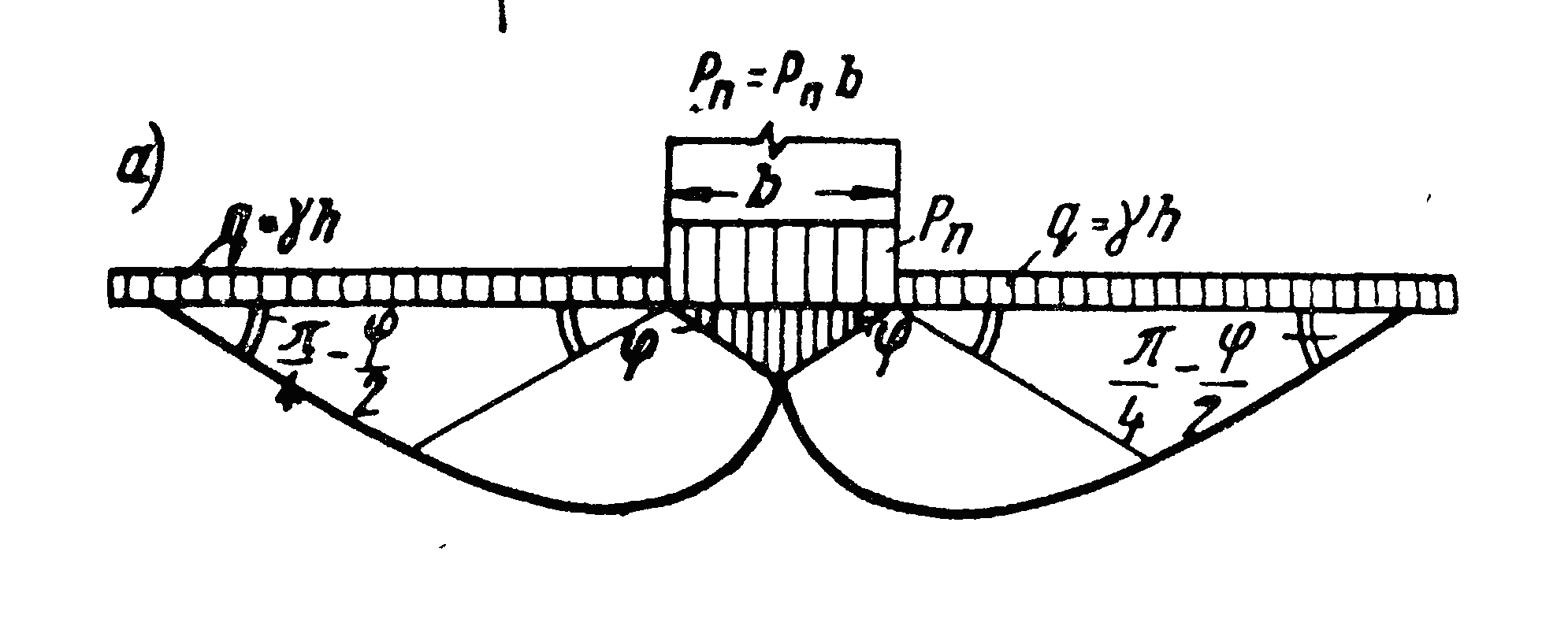
В своем методе расчета несущей способности основания К. Терцаги принял очертание линий скольжения в предположении, что собственный вес грунта равен нулю.

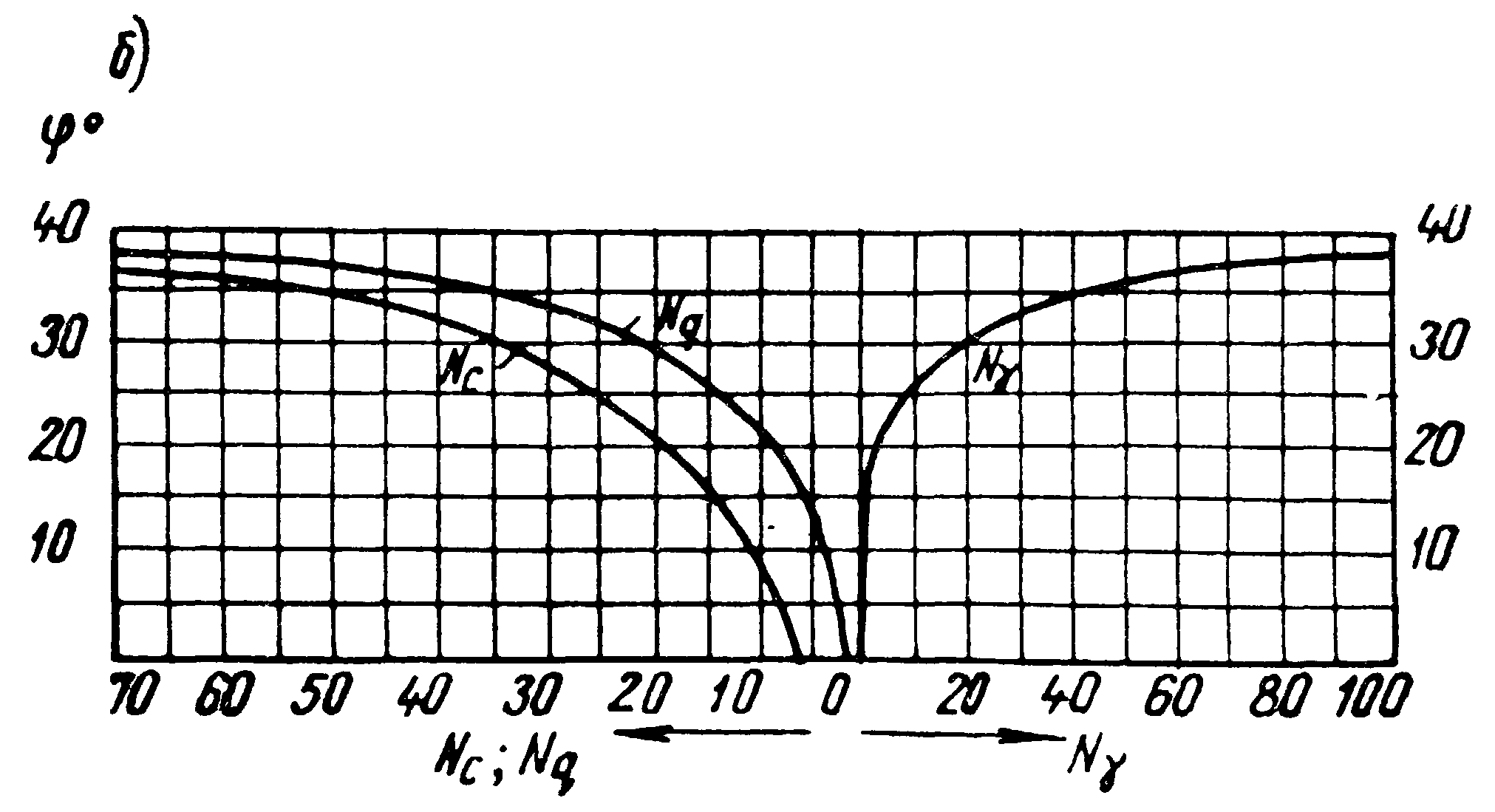
Расчетная схема (а) и графики для определения коэффициентов несущей способности (б) К. Терцаги Цит по Цытович механика грунтов, 1963 г.

Рассматривая равновесие упругого ядра под подошвой фундамента, он получил каноническую трехчленную формулу для определения вертикальной составляющей предельной нагрузки

,

Где , , - коэффициенты несущей способности, зависящие от угла внутреннего трения и определяемые по графикам.

Приведенная формула справедлива для ленточных фундаментов. Для круглых и квадратных фундаментов К. Терцаги на основании данных экспериментов предложил следующие выражения:

Для круглых фундаментов с радиусом а :

Для квадратных фундаментов со стороной 2а:

Для неоднородных, в т.ч. слоистых оснований СНиП и СП рекомендуют расчет по несущей способности выполнять графоаналитическими методами. Наиболее известным из них является метод круглоцилиндрических поверхностей скольжения.

Координаты центра поверхности и её радиус выбираются из довольно большого числа вариантов, для каждого из которых составляется уравнение равновесия сдвигающих и удерживающих сил и определяется требуемая величина сил сцепления. Наиболее опасным признается положение центра, соответствующее максимальной величине сил сцепления. Далее вычисляют коэффициент запаса устойчивости – отношение момента сил, препятствующих сдвигу, к моменту сдвигающих сил:

,

где – отрезок дуги кривой скольжения в пределах i-го отсека призмы скольжения, φ_i, с_i – угол внутреннего трения и сцепление грунта в пределах i-го отсека призмы скольжения, - собственный вес грунта i-го отсека призмы скольжения. Угол положителен при отсчете против часовой стрелки.

Схема к расчету устойчивости оснований по методу круглоцилиндрических поверхностей (из Березанцева, 1970, расчет оснований сооружений).

Кривая выпора считается найденной, если среди нескольких окружностей, проведенных через край фундамента, оказывается обнаруженной окружность, для которой значение коэффициента устойчивости минимальное.

Недостатки данного метода:

1. положение и форма поверхности выпора принимается заранее известными, поэтому при проведении каждого расчета необходимо численное значение коэффициента устойчивости определять для нескольких поверхностей выпора, сравнивать их и выбирать наименьшее;

2. при расчете приблизительно учитывается только вертикальная составляющая полного напряжения в рассматриваемой точке;

3. в расчете не учитывается величина коэффициента бокового давления грунта ξ₀;

4. внешняя нагрузка, приложенная к основанию вне призмы выпора грунта, не учитывается в расчете, хотя может существенно влиять на распределение напряжений;

5. не учитывается трение, возникающее на границе между блоками.

Вследствие всех упомянутых недостатков коэффициент запаса устойчивости не характеризует действительный запас прочности основания, на что указывал ещё В.Г. Березанцев