Обзор современных методов расчета несущей способности основания фундаментов мелкого заложения

Совместная работа системы «сооружение-основание» зависит от множества взаимосвязанных факторов, каждый из которых оказывает влияние на величину несущей способности основания. Однако оценить в расчетах степень этого влияния с достаточной полнотой пока не представляется возможным. Физико-математические модели грунтового массива, на которых базируются существующие расчетные методы, имеют значительные допущения и не отражают в полной мере реальные процессы в грунтовой толще при приложении нагрузки извне.

К настоящему моменту предложено и опробовано в практике проектирования и строительства довольно большое количество методов определения несущей способности основания. Работу по их классификации в свое время независимо друг от друга провели В.А. Флорин и В.Г. Березанцев.

Современные же методы расчета несущей способности оснований фундаментов можно условно разделить на три основные группы:

1) методы, основанные на использовании теории линейно деформируемой среды и поверхностей выпора. Расчет заключается в нахождении их наиболее невыгодного положения.

2) методы, базирующиеся на анализе напряженного состояния грунтового массива – определении глубины развития областей пластических деформаций.

Методы, основанные на использовании теории линейно деформируемой среды и поверхностей выпора

Решение, регламентированное действующими нормами

Действующие нормы разрешают вести расчет несущей способности неоднородных оснований методами, основанными на использовании круглоцилиндрических поверхностей выпора и вычисления соответствующей величины коэффициента запаса устойчивости.

Координаты центра поверхности и её радиус выбираются из довольно большого числа вариантов, для каждого из которых составляется уравнение равновесия сдвигающих и удерживающих сил и определяется требуемая величина сил сцепления. Наиболее опасным признается положение центра, соответствующее максимальной величине сил сцепления. Далее вычисляют коэффициент запаса устойчивости – отношение момента сил, препятствующих сдвигу, к моменту сдвигающих сил:

,

где l_i – отрезок дуги кривой скольжения в пределах i-го отсека призмы скольжения, φ_i, с_i – угол внутреннего трения и сцепление грунта в пределах i-го отсека призмы скольжения, , - удерживающая и сдвигающая составляющие давления от собственного веса грунта i-го отсека призмы скольжения.

(из Березанцева, )

Рис. 1 Схема расчета фундамента на устойчивость методом круглоцилиндрических поверхностей

(из Цытовича, 1963 г)

Кривая выпора считается найденной, если среди нескольких окружностей, проведенных через край фундамента, оказывается обнаруженной окружность, для которой значение коэффициента устойчивости минимальное.

Недостатки данного метода:

1. положение и форма поверхности выпора принимается заранее известными, поэтому при проведении каждого расчета необходимо численное значение коэффициента устойчивости определять для нескольких поверхностей выпора, сравнивать их и выбирать наименьшее;

2. при расчете приблизительно учитывается только вертикальная составляющая полного напряжения в рассматриваемой точке;

3. в расчете не учитывается величина коэффициента бокового давления грунта ξ₀;

4. внешняя нагрузка, приложенная к основанию вне призмы выпора грунта, не учитывается в расчете, хотя может существенно влиять на распределение напряжений;

5. не учитывается трение, возникающее на границе между блоками.

Вследствие всех упомянутых недостатков коэффициент запаса устойчивости не характеризует действительный запас прочности основания, на что указывал ещё В.Г. Березанцев.

Решение а.Н. Богомолова и д.П. Торшина

Инженерный метод, разработанный авторами, для построения наиболее вероятностной поверхности выпора грунта, основан на идеях В.К. Цветкова о построении поверхности обрушения однородного грунтового откоса. Анализ напряженно-деформированного состояния массива грунта провден при помощи методов теории функций комплексного переменного.

Коэффиицент устойчивости в точке грунтового массива и глобальный коэффиицент устойчивости основания по наиболее вероятной выпора определяются формулами

Где - напряжения и угол наклона наиболее вероятной площадки сдвига в рассматриваемой точке грунтового массива

и - удерживающие и сдвигающие силы в точках НВПВ

S – дуговая координата точки НВПВ.

Анализ формул показывает, что глобальный коэффициент устойчивости грунтового основания зависит от всех трех компонент напряжения в каждой точке НВПВ, физико-механичексих свойств грунта и угла наклона касательной к каждой точке наиболее вероятной линии выпора, который может быть определен из выражений.

Так как на величину численных значений напряжений вточках грунтового основания оказывает (отношение модулей общей деформации, если основание слоистое), величина коэфифициента бокового давления, величина отношения ширины фундамента к глубине заложения, величина интенсивности высшего воздействия.

1.2. Методы расчета устойчивости оснований фундаментов мелкого заложения, основанные на теории предельного равновесия грунтовых масс.

Решение в.В. Соколовского

Методы, в которых для определения несущей способности используется теория предельного равновесия, основаны на следующих предположениях:

1) Пока грунт не перейдет в предельное состояние, он считается недеформируемым телом ( );

2) состояние предельного равновесия наступает одновременно во всех точках грунтового массива;

3) В предельном состоянии грунт обладает несжимаемостью, при дальнейшем возрастании нагрузки происходит разрушение грунта (выпор);

4) Сопротивление сдвигу является функцией первого порядка от давления.

Теория предельного равновесия в настоящее время является основной для расчета прочности грунтов. Её преимущество в том, что очертание поверхностей скольжения не задается произвольно, а получается из совместного решения дифференциальных уравнений предельного равновесия (Массо-Кеттера) и уравнений статики.

В общем случае напряженного состояния для плоской задачи, когда единственной объемной силой является объемный вес грунта, уравнения имеют вид.

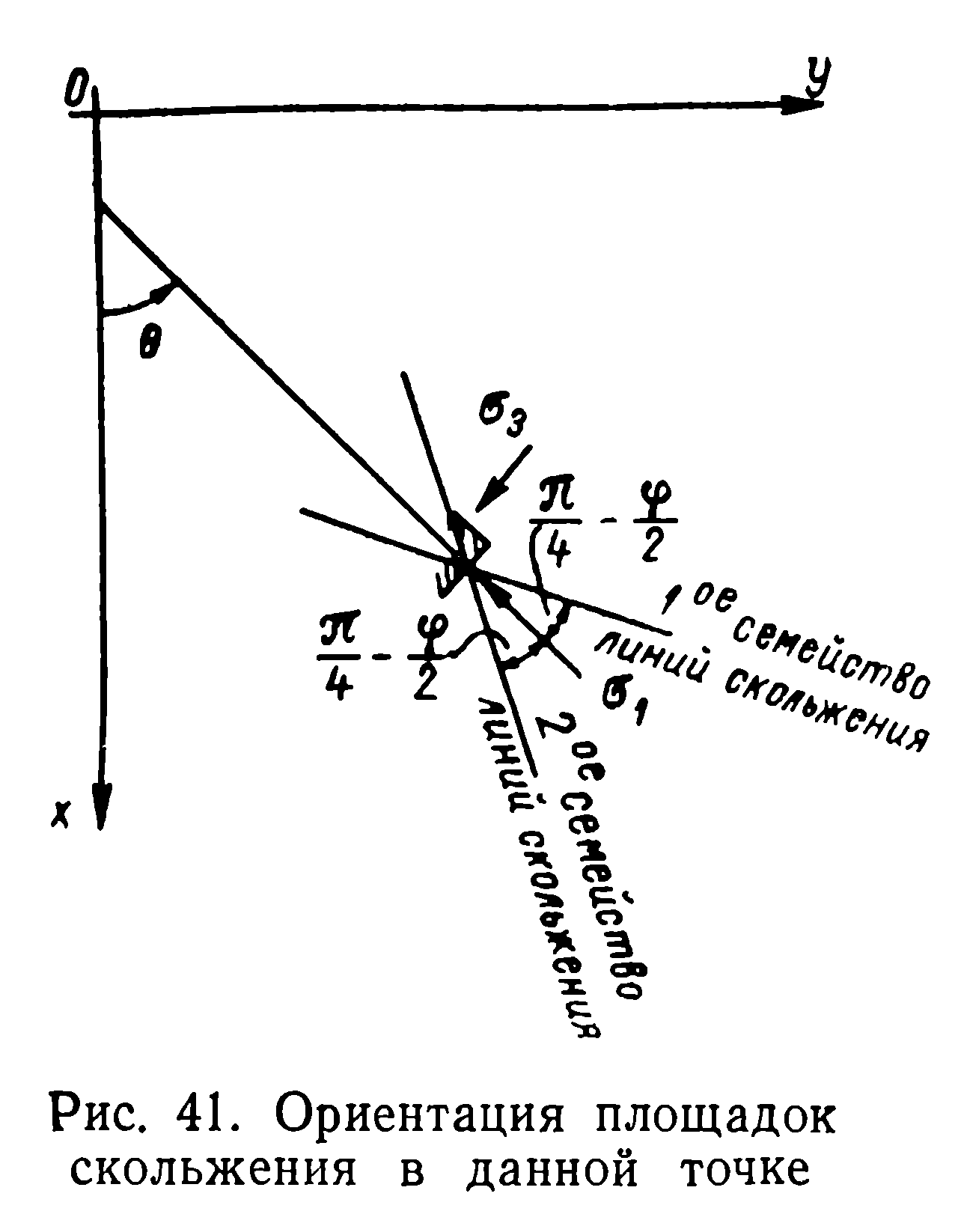
Добавляя к ним условие предельного равновесия в форме,

Совместно решив данные три уравнения, В.В. Соколовский получил два семейства линий скольжения, изображенных на рисунке.

Решение г.Е. Паукера

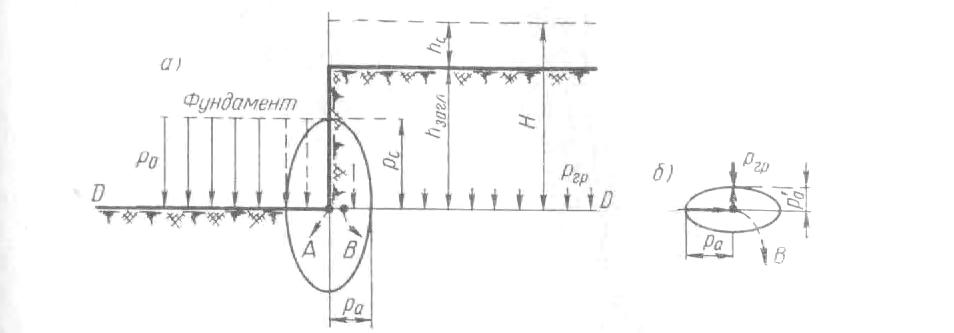
Рис. 2 Расчетная схема к решению Паукера

а — схема действия нагрузки; б— условия работы грунта в точке В, смежной с точкой А

(Маслов, основы механики грунтов, 1968)

В расчетной схеме (рис. 2) рассматриваются условия работы грунта в уровне подошвы фундамента с внешней стороны

Заглубленный фундамент воспринимает нагрузку от сооружения и в крайней точке передает на основание нагрузку p_o. Действие сил сцепления заменяется равными по величине силами внутреннего трения от веса дополнительного слоя грунта толщиной h_с, перекрывающего собой дневную поверхность грунта.

В итоге глубина заложения . Устойчивость грунта основания оценивается в точке B, в которой на грунт действуют сила выпирания и вес грунта, залегающего выше подошвы фундамента.

Напряженное состояние в точке А описывается главными напряжениями p₁ и p₂, для которых в данном случае выполняется условие , , где

Активное давление в точке А вызывает в точке B сопряженное с ним давление, действующее в вертикальной плоскости

В условиях равновесия в точке B выполняется условие

В данных условиях нагрузка на грунт может рассматриваться как критическая. Окончательный вид формулы