Вопросы для самопроверки

1. Сформулируйте теорему существования и единственности дифференци­ального уравнения n -го порядка.

2. Какие уравнения высших порядков допускают понижение?

3. В чем состоит метод вариации постоянных для линейного уравнения вто­рого порядка? Привести пример.

4. Как ищут частные решения неоднородного уравнения, если его правая

часть имеет следующий вид: а) е^2х; б) sin л/Ух; в) х²?

Тема 5.3. Системы дифференциальных уравнений

Учебники: [16, гл. 15, § 6], [22, гл. 3, §§ 1 - 5], [17, гл. 13, §§ 29, 30].

Аудиторная работа: [20, гл. 9, § 3, №№ 9.432, 9.437, 9.442], [15, гл. 12, § 12; Ms 2276, 2279], [30, задание 5, п. 5.1: № 11; п. 5.2: № 6].

Самостоятельная работа: [20, гл. 9, § 3, №№ 9.431, 9.433, 9.438, 9.441, 9.443], [15, гл. 12, § 12, Ms 2275, 2277, 2228], [30, задание 5, п. 5.1: №№ 1 -4,12; п. 5.2: №№1-3, 7].

Указания

Система дифференциальных уравнений первого порядка имеет вид

у^'₁(x) = f(х, y₁,..., y_n)

у^'₂(x) = f₂(х, y₁,..., y_n)

…………..

у^'_n(x) = f_n(х, y₁,..., y_n)

Решением системы на интервале а<х<b называется совокупность функций y_i =φ_i(x)(i=l,...,n), непрерывно дифференцируемых на (a,b) и об­ращающих уравнения системы в тождества относительно xє(a,b).

Дифференциальное уравнение n-го порядка у⁽ⁿ⁾ = f(x, y, y',...,y^(n-1)) можно свести к системе уравнений первого порядка. И, наоборот, систему в большинстве случаев можно свести к уравнению n-го порядка, решая кото­рое можно найти и решение системы.

Пример 5.3.1.

Решение. Возьмем из первого уравнения z = y - y', Отсюда z' = y' - y". Подставив эти выражения во второе, получим у' - у'' = -4у + у- у', или у" -2у' -3у = 0, общим решением этого уравне­ния будет у(х)= С₁е^-х + С₂е^3x.

Отсюда, используя Z = у - у' = C₁e^-x + С₂е^3х + С₁е^-x - 3С₂е^3х, полу­чим Z = 2C₁e^-x - 2С₂е^3х.

Ответ: y = C₁e^-x + С₂е^3х.

Z = 2(C₁e^-x - С₂е^3х).

Такой прием иногда называют методом исключения. Другим, встре­чающимся в приложениях, методом решения системы является нахождение интегрируемых комбинаций [22, гл. 3, § 3].

Вопросы для самопроверки

1. Сформулируйте теорему существования и единственности решения диф­ференциального уравнения первого порядка.

2. Приведите примеры из классов уравнений первого порядка, интегрируе­мых в квадратурах.

3. Какие уравнения высших порядков допускают понижение?

4. В чем состоит метод вариации постоянных для линейного уравнения вто­рого порядка? Приведите пример.

5. Приведите пример решения дифференциальных уравнений нахождения интегрируемых комбинаций.

6. Сформулируйте теорему существования и единственности решения сис­темы уравнений первого порядка.

7. В каком виде ищут частные решения неоднородного уравнения, если его

правая часть имеет следующий вид: а) е^2х, б) sin√3x, в) 2х-1, г) x²+cosx.

После изучения 3, 4, 5 разделов студент должен выполнить контроль­ную работу № 3.

Дополнение 5.1. Образец выполнения и оформления

контрольной работы № 3

"Функции нескольких переменных. Интегрирование функций одной

переменной. Обыкновенные дифференциальные уравнения"

Первые пять заданий контрольной работы № 3, которые относятся к теме "Функции нескольких переменных", подробно рассмотрены в разделе 3, примеры 3.1.1, 3.1.2, 3.2.1, 3.2.2 и 3.3.1.

Примеры решения задач к разделам 4,5

Вычислить интегралы:

1.

Решение. Поделим почленно числитель подынтегральной функции на знаменатель

2.

Решение. Заметим, что подынтегральная функция является неправиль­ной дробью, т. к. степень числителя выше степени знаменателя. Поделим числитель на знаменатель. В результате получим . Разложим правильную дробь на простейшие:

Приравнивая коэффициенты при одинаковых степенях х, получим систему . Решение системы: А = -1;В = 2. Получим разложение . Тогда

3.

4.

5. .

Универсальной тригонометрической подстановкой вычисление инте­грала от тригонометрической функции свелось к вычислению интеграла от дробно-рациональной функции. Разложим подынтегральную дробь на про­стейшие дроби

,

Таким образом,

;

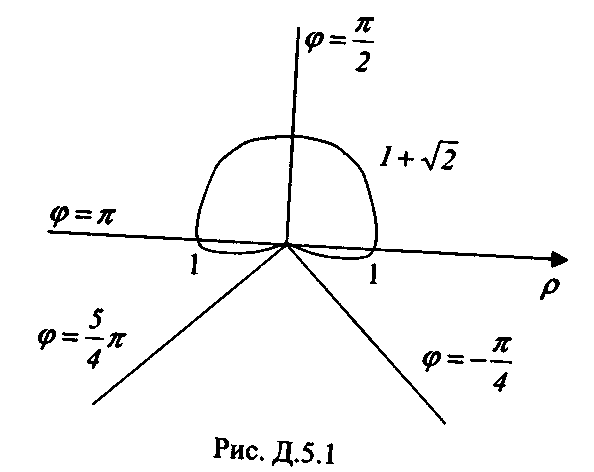
6. Вычислить площадь фигуры, ограниченной линией . Построим кривую (рис.Д.5.1). Область определения ж

при при и ;

7. Исследовать сходимость

.

Решение. На интервале [l,∞) .

Так как , то интеграл сходится, следовательно, по первому признаку сравнения сходится .

8. Решить дифференциальные уравнения первого порядка.

1) (2х³ +3xy²)dx + y³dy = 0.

Решение. Это однородное уравнение. Введем подстановку у=хu(х),

,

, разделим переменные

и проинтегрируем

.

Ответ: .

2) Найти решение уравнения у^’ + ycosx = sinxcosx, удовлетворяющее условию у(0) = 1.

Решение. Это линейное уравнение первого порядка. Сначала рассмот­рим соответствующее однородное уравнение у' + ycosx = 0. Разделим переменные dy/y = -cosxdx и проинтегрируем ln|y| = -sinx + lnС, у = Се^-sinx. Далее методом вариации произвольной постоянной решение исходного уравнения ищем в виде y = φ(x) е^-sinx : φ^’е^-sinx - φе^-sinx cosx + φе^-sinx cosx = cosxsinx, dφ/dx = sinxcosxе^sinx, φ(x) = ∫sinxе^sinx dsinx = ∫ue^udu = ∫ude^u = ue^u - ∫e^udu = e^u(u-1) + C = e^sinx(sinx - 1) +C. Таким образом, общее ре­шение имеет вид y = sinx - l + Ce^-sinx. Удовлетворим условию у(0)= -1 + С = 1, С = 2.

Ответ: y = sinx - l + 2e^-sinx.

9. Решить уравнения второго порядка.

1) yy^” = y^’2.

Решение. Уравнение не содержит явно х, поэтому его порядок пони­жается подстановкой у '=z(y), причем

.

Приравниваем к нулю каждый из сомножителей левой части:

a) z = 0, y^’ = 0, y = C;

б) ,

.

Ответ: y = C₂e^C/x.

2) Найти решение уравнения у"+y = ctgx, удовлетворяющее условиям .

Решение. Рассмотрим соответствующее однородное уравнение у"+у = 0, его характеристическое уравнение х² + 1 = 0, откуда x_1,2 = ±i и общее решение однородного уравнения будет у = С₁sinx + С₂cosч. Далее по методу Лагранжа решение неоднородного уравнения в виде у = φ₁(x)sinx + φ₂(x)cosx, причем функции φ₁(x) и φ₂(x) определяются из системы

;

;

.

Итак, общее решение неоднородного уравнения имеет вид

.

Удовлетворим начальным условиям:

.

Ответ: .

10. Решить систему

Решение. Методом исключения получаем х - 4х - 5х = -4е^-t + 2e^2t, при этом 2у = – х – е^-t. Соответствующее однородное - 4 - 5х = 0 имеет решение

.

Частное решение неоднородного следует искать в виде x_z = Atе^-t + Bе^2t (-1 - корень характеристического уравнения). Дифференцируя _z = -Atе^-t + Aе^-t + 2Bе^2t, _z = Atе^-t - 2Aе^-t + 4Bе^2t, и подставляя в уравнение, получим

-6Aе^-t – 9Bе^2t = -4е^-t + 2е^2t,

следовательно, A = 2/3, B = -2/9, x_z = 2/3tе^-t – 2/9е^2t.

Тогда

.

Ответ: ,