Тема 3.2. Экстремум функции
Учебники: [16], [17].
Аудиторная работа: [3, №№ 3259, 3292].
Самостоятельная работа: [3, №№ 3260, 3293].
Точка М0
называется точкой локального максимума
(минимума), если значение функции в этой
точке будет наибольшим (наименьшим) из
окрестности точки М0.
Необходимое условие существования
локального экстремума:
,
или
.
Сформулируем
достаточное условие для функции двух
переменных. Введем обозначения:
;
;
.
Если D = AC – В2 > 0, то в точке М0 – локальный экстремум, причем, если А > 0 – локальный минимум, а если А < 0 – локальный максимум.
Для функций многих переменных, т. е. 3,4,…,n, достаточным условием будет условие знакопостоянства второго дифференциала.
Второй дифференциал представляет собой квадратичную форму, а условие знакопостоянства квадратичной формы дает критерий Сильвестра.
Если d2f > 0, то в точке М0 – локальный минимум, если d2f < 0 ‑ локальный максимум.
Функция u
= f(р) имеет
условный максимум (минимум) в точке Р0,
если существует такая окрестность
точки Р0, для всех точек
Р которой
,
удовлетворяющих уравнениям связи
выполняется
неравенство
.
Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа.
.
Пример 3.2.1. Найти точки экстремума функции
.
Решение. Из необходимого условия экстремума найдем точки, подозрительные на экстремум:
Отсюда
,
,
.
Проверим для точки
, достаточное
условие. Для этого найдем вторые
производные:
;
;
;
Экстремум есть и т. к. А > 0, то это — локальный минимум.
Ответ. В точке
локальный минимум
.
Пример 3.2.2.
Найти экстремум функции
при условии
.
Решение. Для нахождения условного экстремума составим функцию Лагранжа:
.
Удовлетворим необходимому условию существования экстремума.
,
,
,
Разрешая эту
систему, получаем
;
;
;
.
Так как
;
;
,
то
1.
— локальный минимум;
2.
— локальный максимум.
Следовательно, в
точках
,
,
— min, а в точках
,
,
локальный максимум.
Тема 3.3. Геометрические приложения функций нескольких переменных
Учебники: [16], [17].
Аудиторная работа: [3, №№ 3412, 3416].
Самостоятельная работа: [3, №№ 3414, 3417].
Уравнение касательной плоскости, в случае явного задания поверхности, т. е. z = z(x,y) в точке М0(х0,у0) записывается
.
Если поверхность задана в неявном виде F(x,y,z), то нормаль к касательной плоскости имеет вид
Прямая называется нормальной к поверхности в точке, если она проходит через эту точку и перпендикулярна к касательной плоскости, проходящей через эту же точку.
В случае явного задания поверхности нормальная прямая имеет вид
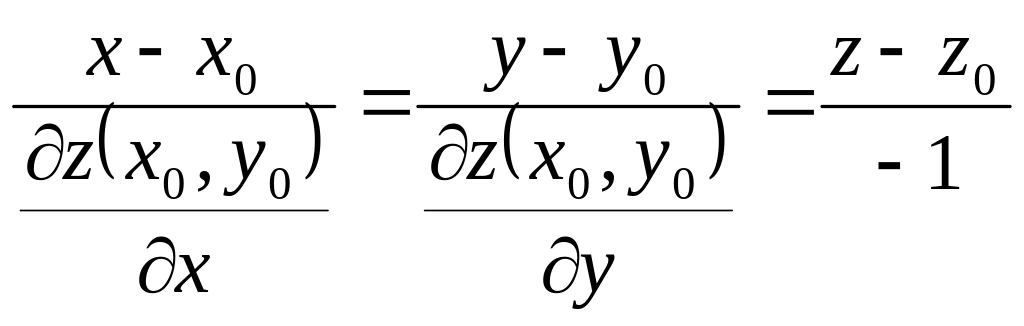
В случае неявного задания поверхности
Пример 3.3.1. Написать уравнение касательной плоскости и нормальной прямой к поверхности х4у + 2х2у3 + xyz2 +ez =3 в точке M0(l,l,0).
Решение.
Уравнение поверхности задано в неявном
виде F(x,y,z) = х4у + 2х2у3 + xyz2 + ez – 3
= 0. Найдем
нормаль к касательной плоскости:
.
Найдем частные производные от функции F в точке М0:
,
,
,
тогда
и уравнение плоскости в точке М0
запишется
8(х – l) + 7(y – 1) + z = 0, или 8х + 7у + z = 15.
Уравнение нормальной прямой к поверхности в точке М0
.