Дополнение 2.1. Образец выполнения и оформления контрольной работы № 2 "Дифференциальное исчисление функции одной переменной"
1. Найти пределы:
1)
Ответ:
;
2)
.
Ответ:
;
3)
.
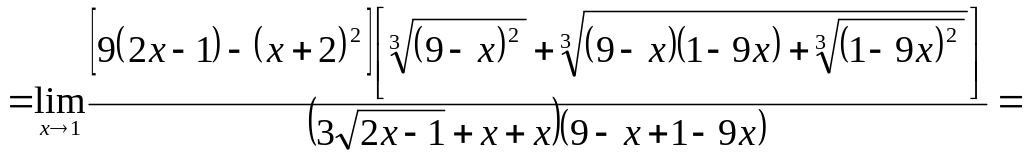
Ответ:
;
4)
,
обозначим
,
тогда
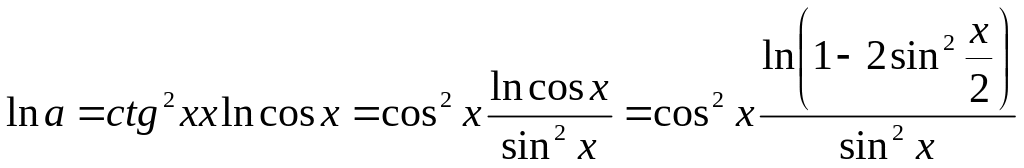
5) найдем предел этого выражения
,
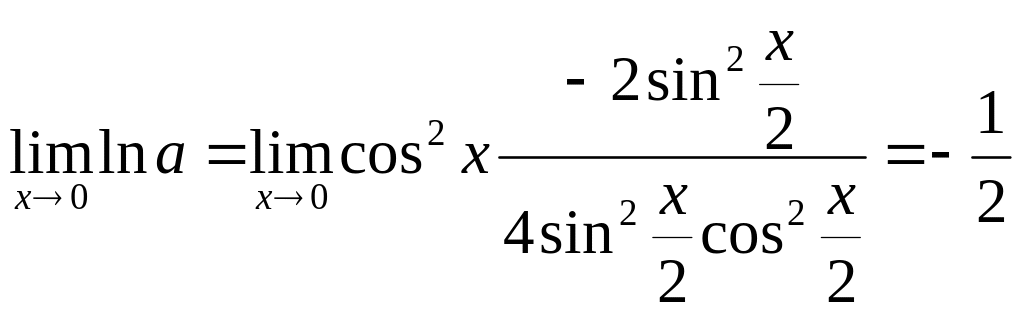поэтому
Ответ:
.
2. Найти производную
данной функции
и ее значение при х = а.
;
;
Ответ:
;
.
3. Найти производную y = (2 + cos x)2. Так как ln y = x ln(2 + cos x), то дифференцируя, получим:
,
или
Ответ:
.
4. Найти уравнение
касательной к кривой
,
в точке M(l,2). Уравнение касательной
у – у0 = к(х – х0),
где к = у’(х0).
.
Найдем значение
t, соответствующее
точке М: при х = 1, имеем
,
,
,
,
т.е.
.
Значит
,
таким образом, у – 2 = 3(x – l).
Ответ: y = 3x – 1.
5. Найти
,если
,
y = tg
t – 1.
;
.
Ответ:
,
.
6. Найти пределы по правилу Лопиталя:
1)
.
Ответ:
;
2)
,
имеем неопределенность
.
Пусть
,
тогда
,
значит,
,
следовательно,
.
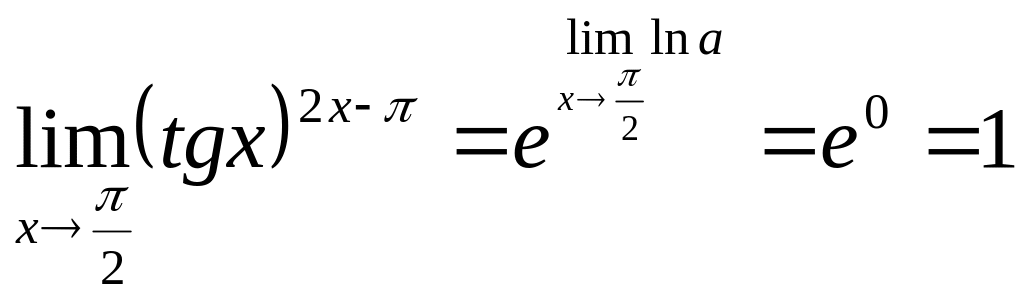Ответ: 1.
3)
,
.
Ответ: 1.
7. Разложить по формуле Тейлора f(x) = ln(2 + х – х2) в окрестности точки х0 = 1.
Решение.
.
,
;
.
Докажем по методу математической индукции:
.
Подставим в формулу
значения производных,
получим:
,
где
Остальные задания контрольной работы № 2 связаны с построением графиков функций. Эти вопросы полностью освещены в теме 2.3, в пункте "Построение графиков".
Раздел 3; Функции нескольких переменных Тема 3.1. Частные производные
Учебники: [16], [17].
Аудиторная работа: [3, №№3043 - 3083 нечет., 3124 - 3134 чет., 3145, 3147, 3149, 3181 - 3201 нечет.].
Самостоятельная работа: [3, №№3044 - 3084 чет., 3125 - 3135 нечет, 3146, 3148, 3150, 3152, 3182 - 3200 четные].
Назовем приращение
функции по одной из переменных
частным приращением функции по переменной
x.
Предел отношения частного приращения к приращению аргумента называется частной производной и обозначается
.
Вычисляется частная производная по тем же правилам, что и производная от функции одной переменной, при этом остальные переменные считаются неизменными.
Если функция u
= f(x,y,z), зависящая от трех переменных,
которые, в свою очередь,
зависят еще от переменных t и
,
т. е.
и
,
тогда
,
.
Полный дифференциал первого порядка для функции многих переменных имеет вид
.
Производные высших
порядков вводятся индуктивно, т. е.
и т.п.
Производные
,
и т.д. называются смешанными произвонымн.
Полный дифференциал n–го порядка вычисляется по формуле
.
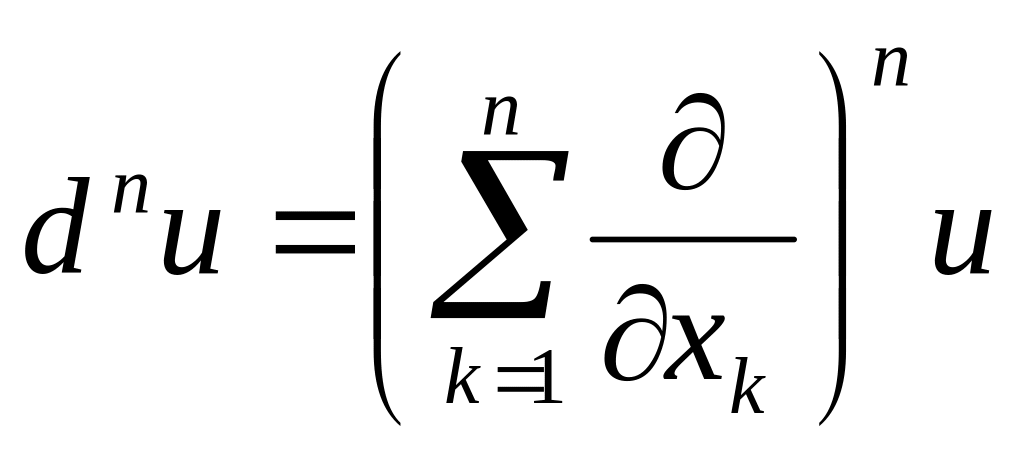Если взять некоторое
направление
,
то производная от функции в этом
направлении вычисляется следующим
образом:
,
где
Пример 3.1.1.
Вычислить производную функции
в точке М0(1,1)
в направлении вектора
.
Решение. По
определению
найдем
в точке M0(1,l). Для этого
вычислим частные производные.
,
Из вектора сделаем единичный вектор
и окончательно получим:
.
Ответ:
.
Пример 3.1.2. Найти второй дифференциал функции z, которая задана неявно: х3у + yz + z3 = 3.
Решение. По определению
.
От обеих частей
функции, заданной в неявном виде, возьмем
производную по х:
,
а затем еще раз производную по x:
.
Из этого равенства найдем
:
.
Найдем смешанную
производную
,.
Равенство
дифференцируем по у:
;
.
От функции
возьмем производную по у: 
.
затем еще раз по у.
Из равенств
;
получим
,
и окончательно запишем выражение для второго дифференциала
.