Вопросы для самопроверки

1. Дайте определение функции. Что называется областью определения функции?

2. Перечислите основные способы задания функции. Приведите примеры.

3. Перечислите основные элементарные функции и постройте их графики.

4. Что такое бесконечно малая величина и каковы ее свойства?

5. Сформулируйте определения пределов последовательности, переменной величины и функции.

6. Дайте определение непрерывности функции в точке и на отрезке.

7. Покажите, что бесконечно малые sinx, arcsinx, tgx, arctgx (при ) эквивалентны друг другу.

Тема 2.2. Производная и дифференциалы

Учебники: [16, гл. 4, §§ 1 - 3], [4, гл. 4, §§ 4.1 - 4.11], [17, гл. 3].

Аудиторная работа: [20, гл. 5, § 1.2, №№ 5.11, 5.24, 5.40, 5.50, 5.60, 5.86, 5.148, 5.171, 5.187, 5.206, 5.225, 5.233, 5.244, 5.287, 5.295, 5.298, 5.309], [15, гл. 6, §§ 1 - 12, №№ 860, 909, 918, 940, 957, 977, 998, 1001, 1025 (2), 1051, 1068 (3), 1085 (2), 1088], [33, гл. 2, №№ 1.9, 1.12, 7.3, 8.7, 9.7, 9.9, 10.10, 11.6, 12.7, 12.10, 13.3, 14.0, 14.7, 15.3].

Самостоятельная работа: [20, гл. 5, § 1.2, №№ 5.4 - 5.12, 5.21 - 5.90, 5.144 - 5.159, 5.168 - 5.183, 5.184 - 5.193, 5.205, 5.215, 5.222 - 5.226, 5.229 -5.232, 5.235 - 5.246, 5.285 - 5.289, 5.290 - 5.297, 5.298, 5.303 - 5.308], [15 гл. 6, §§ 1 - 12, №№ 848 - 904, 905 - 919, 937 - 947, 963 - 975, 991 - 997, 1000, 1021 - 1025, 1044 - 1048, 1064 - 1069, 1083, 1085], [33, гл. 2, №№ 1.1 - 14.12].

Указания

Перед изучением этого раздела студент должен свободно владеть понятиями функции, предела и бесконечно малой величины, уметь раскрывать неопределенности в пределах вида , , , , исследовать функцию на непрерывность.

Определение производной. Производной функции у = f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю: .

Обозначения: .

Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.

Геометрический смысл производной состоит в том, что производная равна угловому коэффициенту касательной к графику функции в точке х₀. Поэтому — уравнение касательной, а - уравнение нормали.

Основные свойства производной, а также производные основных элементарных функций следует выписать и выучить наизусть, так как они будут применяться систематически. С их помощью можно вывести производную любой элементарной функции.

Пример 2.2.1.

,

но ,

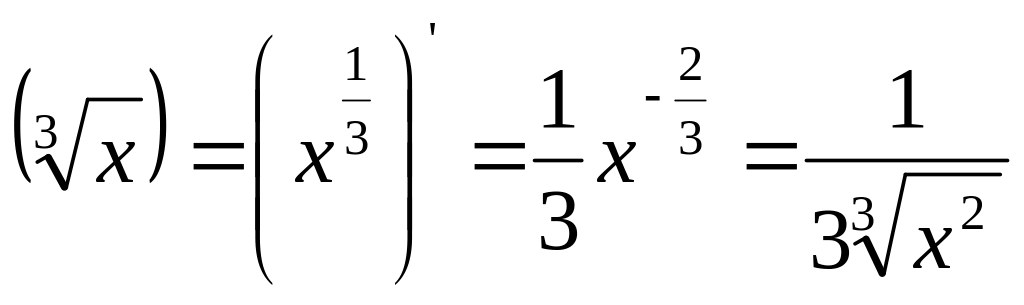а по формуле для производной сложной функции —

.

Отсюда, после вынесения общего множителя за скобки, получим

.

В некоторых случаях перед вычислением производной полезно предварительное дифференцирование. Пусть, например:

Пример 2.2.2. , тогда . Дифференцируем . Отсюда окончательно получим .

Дифференциал и его связь с приращением. Дифференциалом функции называется произведение производной на приращение аргумента. Обозначение dy, т. е. . Дифференциал независимого переменного равен его приращению.

Приращение функции при , т. е. дифференциал есть главная линейная часть приращения функции.

Дифференциал применяется в приближенных вычислениях. Заменяя приращение f(a + h) – f(a) дифференциалом f'(a)h, будем иметь приближенные формулы. Примеры:

Пример 2.2.3. ,

Пример 2.2.4. ,

Пример 2.2.5. .

Пусть известно, что ln2 = 0,693, тогда ; по таблицам , т. е. ошибка меньше 0,2%.

Иногда перед применением формул требуется предварительное преобразование величины, которую нужно вычислить.

Пример 2.2.6.

.

По таблицам , т.е. ошибка <0,01%.

Производные высших порядков. Производной второго порядка от функции y = f(x) называется производная от ее первой производной, т. е.

Вообще, производной n–го порядка (или n–й производной) называется производная от производной (n-1) порядка, т. е. .

Пример 2.2.7. . Имеем , тогда

.

Дифференциалы высших порядков. Дифференциал второго порядка — это дифференциал от дифференциала, т. е. . Аналогично, и т. д.

Пример 2.2.8.