Собственные числа и собственные векторы матрицы линейного преобразования (оператора)

Всякий ненулевой вектор называется собственным вектором линейного преобразования, если

, (1.5.4)

где – некоторое число, называемое собственным значением (числом) линейного преобразования.

Если матрица А имеет вид (1.5.2), то равенство (1.5.4) записывается в виде системы линейных алгебраических уравнений

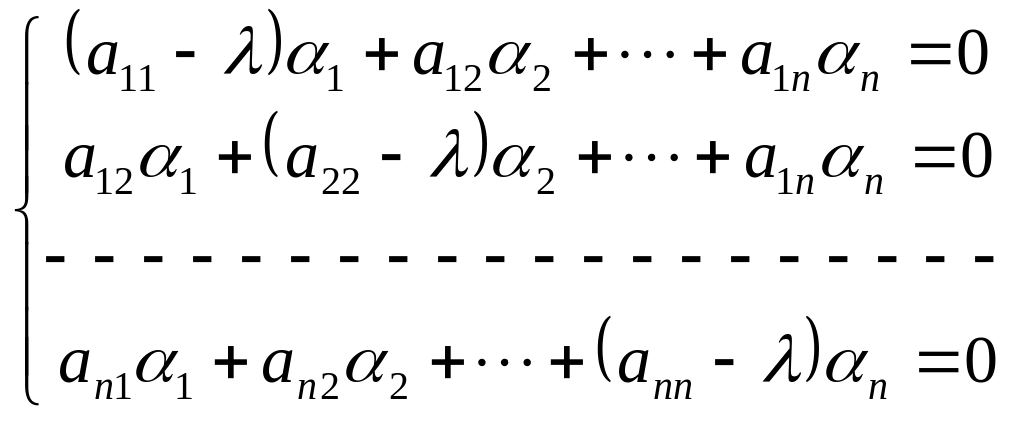, (1.5.5)

Система (1.5.5), однородная СЛАУ, имеет отличные от нуля (нетривиальные) решения тогда и только тогда, когда определитель равен нулю. Отсюда следует, что

. (1.5.6)

Уравнение (1.5.6) называется характеристическим уравнением матрицы данного линейного преобразования. Каждый действительный корень  уравнения (1.5.6) является собственным числом. Соответствующие собственному числу координаты собственного вектора находятся из системы (1.5.5) методом, изложенным в теме 1.1 (см. пример 1.1.11).

Пример 1.5.4. Найти собственные числа и собственные векторы матрицы линейного преобразования

.

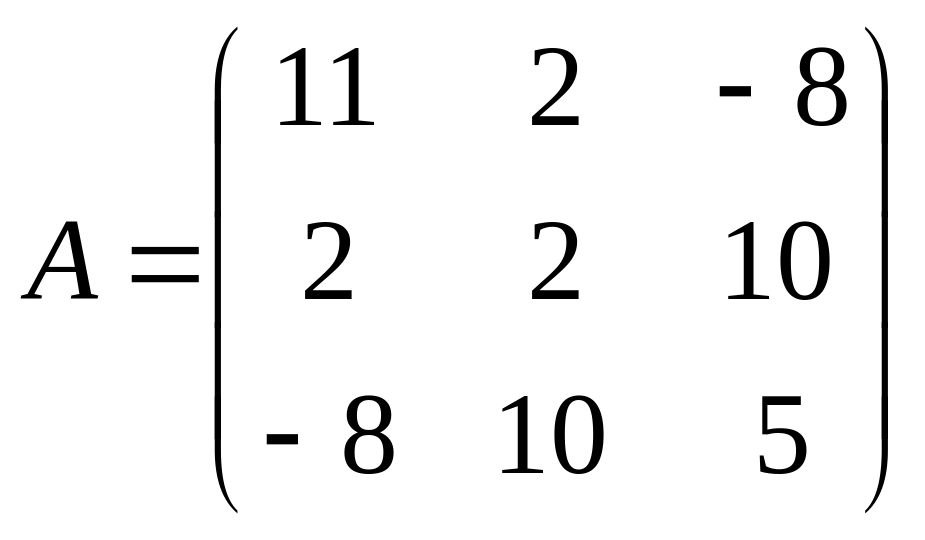Решение. Система однородных линейных алгебраических уравнений (1.5.5) для нахождения собственных векторов имеет вид

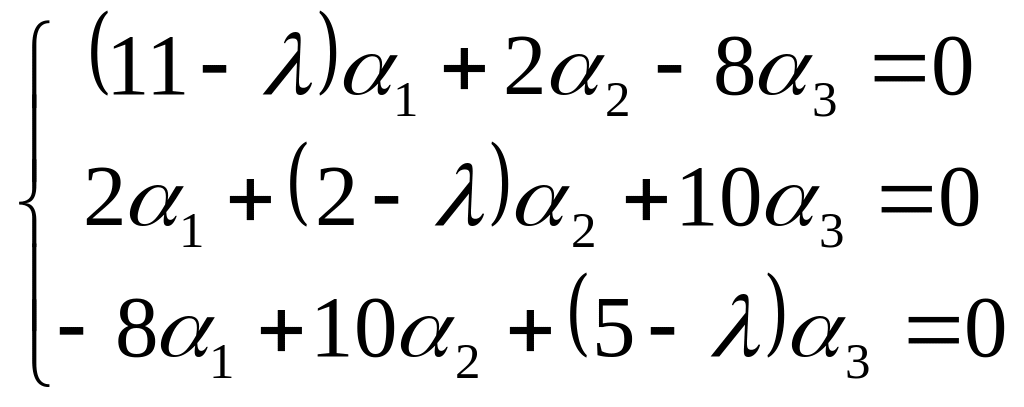(1.5.7)

Вычислим определитель (1.5.6) и решим соответствующее характеристическое уравнение

.

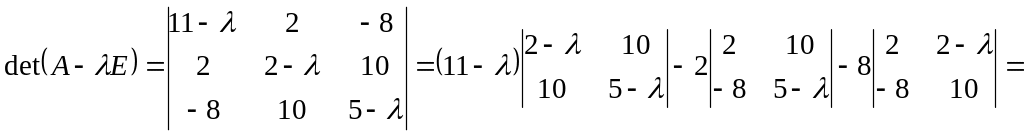
Характеристическое уравнение имеет вид , а его решение . Найденные значения подставим в систему (1.5.7):

Решение этой системы , а соответствующий единичный вектор .

При ; при .

Решения систем линейных уравнений рассмотрены в теме 1.1 (см. пример 1.1.11).

Необходимо отметить следующие свойства собственных значений и собственных векторов симметрической матрицы:

1. Корни характеристического уравнения вещественной симметрической матрицы вещественны;

2. Собственные векторы вещественной симметрической матрицы, отвечающие различным собственным значениям, - ортогональны (проверьте на собственных векторах матрицы примера 1.5.4).

Вопросы для самопроверки

1. Приведите примеры n–мерных векторов.

2. Что такое линейное векторное пространство? Какое пространство называется евклидовым?

3. Что такое базис в n–мерном пространстве?

4. Как определяется линейное преобразование?

5. Докажите неравенство Коши‑Буняковского.

6. Докажите неравенство .

7. При каком условии матрица линейного преобразования имеет диагональный вид?

8. Сформулируйте алгоритм нахождения собственных векторов.

Тема 1.6. Квадратичные формы. Приведение к каноническому виду уравнений линии и поверхности второго порядка

Учебники: [1, гл. 3, § 4], [10, гл. 7, § 2], [16, гл. 11, § 3].

Аудиторная работа: [2, №№> 9.4 (1, 3), 11.22 (2)], [7, гл. 3, §§ 5, 6, № 63 (1, 2)], [20, ч. 1, гл. 4, § 3, №№ 4.226, 4.227, 4.233], [28, занятия 16 (16.2.6 (а, б)), 17(17.2.1, 17.2.2)].

Самостоятельная работа: [2, №№ 9.4 (4 - 6), 11.22 (2)], [7, гл. 3, §§ 5, 6, № 63 (3 - 5)], [20, ч. 1, гл. 4, § 3, №№ 4.228, 4.289, 4.234], [28, задания 16 (16.3.3 (а, б, в)), 17 (17.3.2, 17.3.3, 17.3.4 (а, б, в))].

Квадратичной формой от трех переменных дг, у, z называется однородный многочлен второй степени относительно этих переменных.

. (1.6.1)

Если учесть, что а₁₂=а₂₁, а₁₃=a₃₁, a₂₃ =а₃₂, то F(x,y,z) записывается в виде

.

Матрица

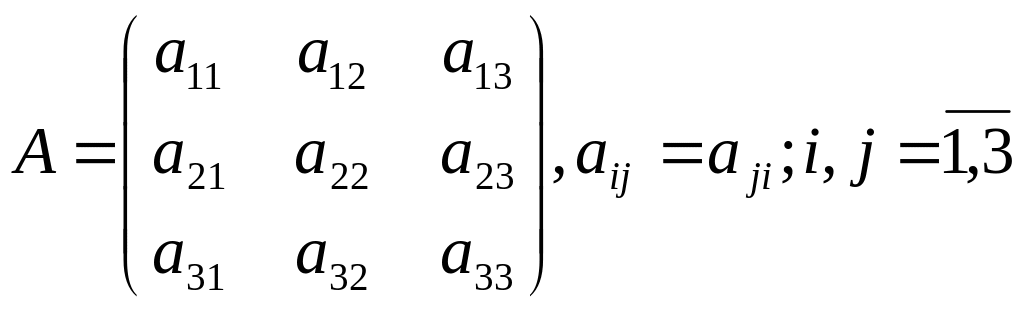. (1.6.2)

называется матрицей квадратичной формы. Квадратичная форма имеет канонический вид, если она содержит члены только с квадратами переменных, т. е . Матрица (1.6.2) квадратичной формы (1.6.1) будет иметь диагональный вид, если в трехмерном пространстве перейти к новому базису, состоящему из собственных векторов (см. тему 1.5) матрицы А, при этом на главной диагонали будут стоять собственные числа матрицы А.

Квадратичная форма в новом базисе будет иметь вид

, (1.6.3)

а ее матрица

.

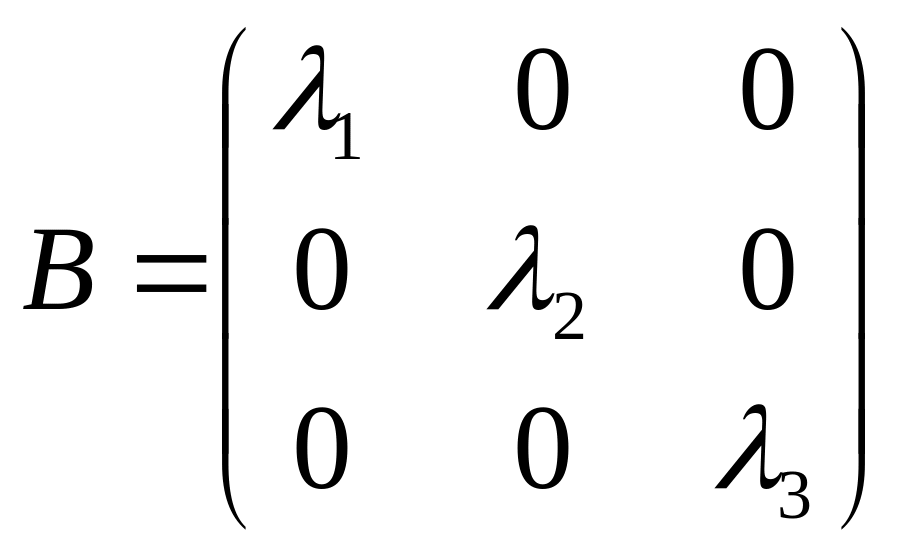В случае двух переменных х, у квадратичная форма F(x,y) имеет вид

, (1.6.4)

а ее матрица

, (1-6-5)

причем а₁₂ = а₂₁.

Методы приведения квадратичной формы к каноническому виду применяются при решении задач на приведение к каноническому виду уравнений кривых второго порядка

и уравнений поверхностей второго порядка

.

Канонические уравнения основных кривых второго порядка были рассмотрены в теме 1.4 в формуле (1.4.6).

Поверхности второго порядка делятся на центральные и нецентральные. Канонические уравнения некоторых поверхностей второго порядка приведены ниже.