
- •1. Идеальные газы. Закон Менделеева-Клапейрона. Параметры вещества.
- •2. Первый закон термодинамики. Формулировка. Математическое выражение.
- •Частные случаи первого закона термодинамики для изопроцессов
- •Формула кпд теплового двигателя:
- •Цикл Карно для тепловой машины
- •2. 2 Закон термодинамики. Формулировка. Понятие процесса, цикла. Прямые и обратные циклы.
- •4. Условия получения работы в тепловых двигателях.
- •.2.Закон Фурье
- •9.3.Коэффициент теплопроводности
- •Условия однозначности процессов теплообмена, закон Ньютона - Рихмана
- •Дифференциальные уравнения теплопроводности в твердом теле
- •Теплопроводность через однослойную и многослойную плоскую стенки при граничных условиях первого рода
- •15. Уравнение теплового потока через плоскую стенку при граничных условиях первого рода
- •16. Уравнение теплового потока через однослойную цилиндрическую стенку при граничных условиях первого рода
- •17. Уравнение теплового потока через однослойную цилиндрическую стенку при граничных условиях третьего рода
- •18. Уравнение теплового потока через многослойную цилиндрическую стенку при граничных условиях первого рода
- •25) Теплоотдача при кипении.
- •26. Теплоотдача при кипении.
- •27. Теплоотдача при конденсации.
- •28. Теплообменные аппараты. Классификация. Схемы движения сред.
- •1. Теплообменные аппараты.
- •2. Классификация теплообменных аппаратов.
- •29. Основы теплового расчета рекуперативных теплообменников.
Условия однозначности процессов теплообмена, закон Ньютона - Рихмана
Для каждого конкретного случая к дифференциальному уравнению теплопроводности добавляют математические условия или ряд дополнительных уравнений, называемых условиями однозначности.Условия однозначности включают в себя геометрические, физические, временные и граничные условия.
Геометрические условия характеризуют геометрические и линейные размеры тела, участвующего в процессе теплообмена.
Физические условия характеризуют физические свойства тела, среды или задается закон внутреннего тепловыделения.
Временные или начальные условия характеризуют особенности протекания процесса во времени или распределение температуры внутри тела в начальный момент времени
Граничные условия характеризуют процессы теплообмена между поверхностью тела и окружающей средой.
Граничные условия задаются несколькими возможными случаями:
I рода - задается распределение температуры на поверхности тела: Тп =f (x, y, z, т)
II рода - задается распределение теплового потока на поверхности тела: qH = f (x, y, z, т).
III рода - задаются температура окружающей среды Тс и закон теплообмена между средой и поверхностью тела, чаще всего используется закон теплообмена Ньютона:
Q = а(Тп — Тс) или —X(dJ/dn) = а(Тп — Тс).
IV рода (условия сопряжения) - характеризуют процессы теплопроводности между соприкасающимися поверхностями различных тел, когда температура в точке сопряжения тел одинакова, но тепловые потоки разные.
Закон Ньютона – Рихмана
Плотность теплового потока (выражается вВт/м²) на границе тел пропорциональна их разности температур (так называемый температурный напор):
![]()
где
![]() —
плотность теплового потока при перепаде
температур на 1K, измеряется вВт/(м²·К)
—
плотность теплового потока при перепаде
температур на 1K, измеряется вВт/(м²·К)
Закон Ньютона служит одним из видов граничных условий, которые ставятся в задачах теплопроводности.
![]()
Дифференциальные уравнения теплопроводности в твердом теле
Дифференциальное уравнение теплопроводности Фурье для изотропного твердого тела в декартовой системе координат (установлен Ж.Б. Фурье в 1822 г.) имеет вид:
![]()
Если температурное поле стационарное – имеем дифференциальное уравнение Пуассона:
![]() При
отсутствии внутренних источников
теплоты, когда тепловыделение W равно
нулю, имеем дифференциальное уравнение
Лапласа:
При
отсутствии внутренних источников
теплоты, когда тепловыделение W равно
нулю, имеем дифференциальное уравнение
Лапласа:
![]() Дифференциальные
уравнения Фурье, Пуассона и Лапласа
могут быть
двумерными, когда температура
зависит от двух любых координат, и
одномерными, когда температура зависит
только от одной координаты пространства.
Дифференциальные
уравнения Фурье, Пуассона и Лапласа
могут быть
двумерными, когда температура
зависит от двух любых координат, и
одномерными, когда температура зависит
только от одной координаты пространства.
Теплопроводность через однослойную и многослойную плоскую стенки при граничных условиях первого рода
Рассмотрим
плоскую стенку толщиной δ. Пусть на
левой поверхности стенки поддерживается
температура t1, а на правой
температура t2. Теплопроводность
λ материала стенки практически постоянна.
Внутри стенки нет источников теплоты.
Требуется определить температурное
поле в стенке и плотность теплового
потока q.
Согласно закону Фурье,
тепловой поток проходящий через стенку,
прямо пропорционален поверхности,
разности температур t1 и t2
и обратно пропорционален толщине δ.
Тогда
![]() Плотность
теплового потока q (Вт/мК) определяют из
выражения
Плотность
теплового потока q (Вт/мК) определяют из
выражения
![]() Отношение
Отношение
![]() называется
тепловой проводимостью стенки, а обратная
величина δ/λ (м2К/Вт) - термическим
сопротивлением (Rλ)
теплопроводности.
называется
тепловой проводимостью стенки, а обратная
величина δ/λ (м2К/Вт) - термическим
сопротивлением (Rλ)
теплопроводности.
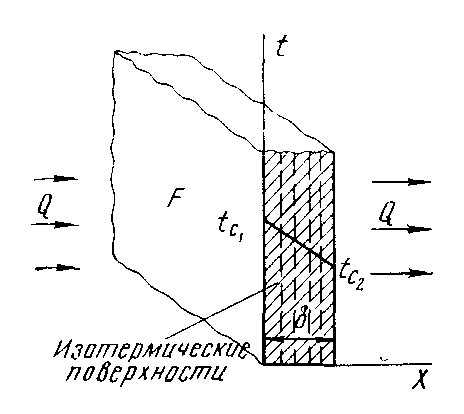 Схема
передачи теплоты теплопроводностью
через плоскую однослойную стенку
Передача
теплоты может осуществляться через
многослойную плоскую стенку. Примером
может служить теплоизоляционное
ограждение стационарных холодильных
камер. Рассмотрим определение теплового
потока теплопроводностью через
многослойную стенку (рис. 4.4).
Схема
передачи теплоты теплопроводностью
через плоскую однослойную стенку
Передача
теплоты может осуществляться через
многослойную плоскую стенку. Примером
может служить теплоизоляционное
ограждение стационарных холодильных
камер. Рассмотрим определение теплового
потока теплопроводностью через
многослойную стенку (рис. 4.4).
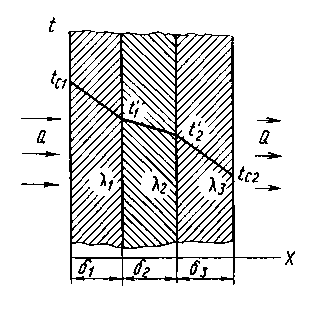 Схема
передачи теплоты теплопроводностью
через плоскую многослойную стенку
В
этом случае термическое сопротивление
многослойной стенки определится как
сумма термических сопротивлений всех
слоев:
Rλ =δ/λ1+δ2/λ2+…+δn/λn
Плотность
теплового потока равна
Схема
передачи теплоты теплопроводностью
через плоскую многослойную стенку
В
этом случае термическое сопротивление
многослойной стенки определится как
сумма термических сопротивлений всех
слоев:
Rλ =δ/λ1+δ2/λ2+…+δn/λn
Плотность
теплового потока равна
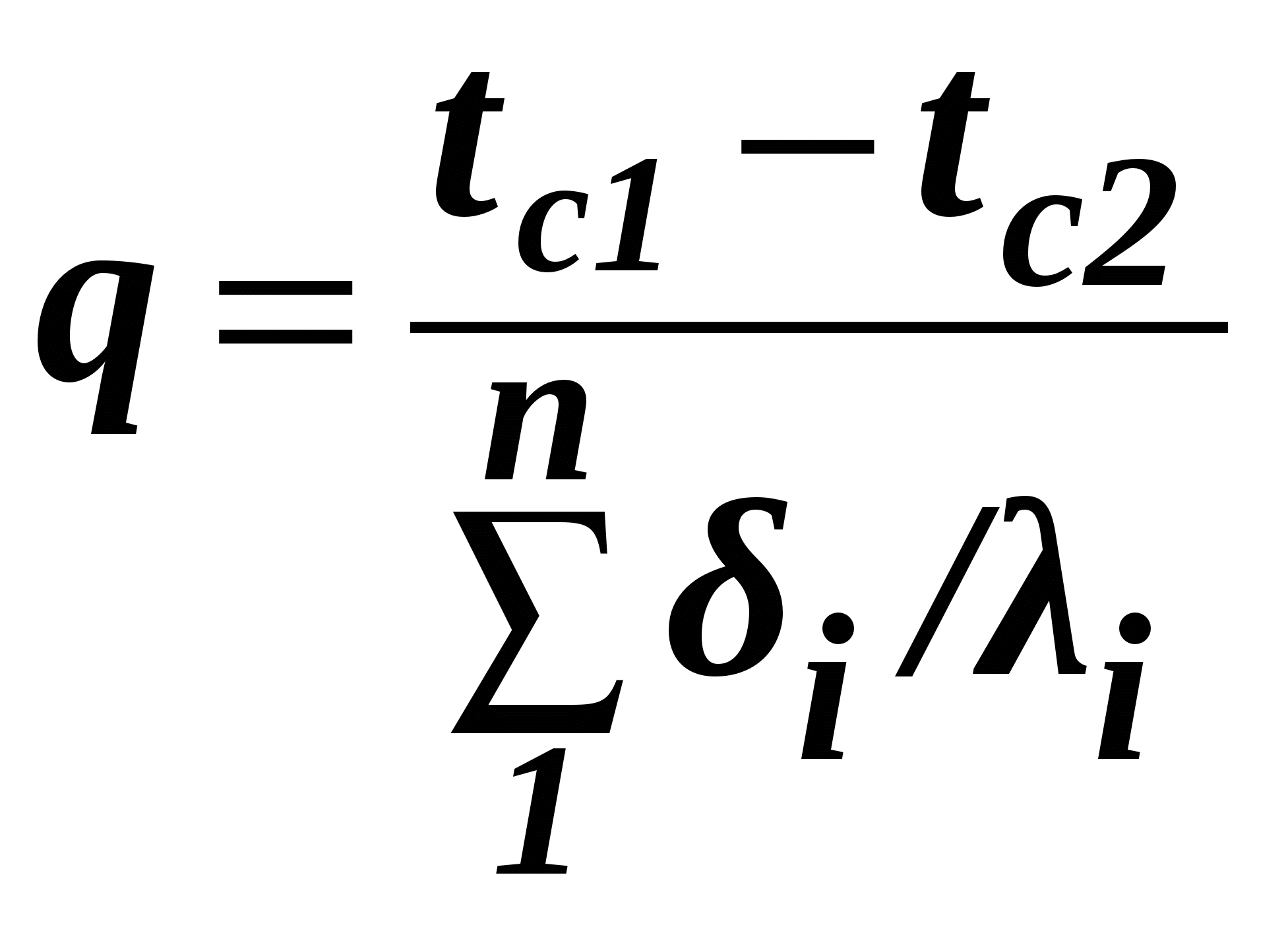 Распределение
температур в пределах каждого слоя –
линейное, однако в различных слоях угол
наклона температурной прямой отличается:
более резко изменяется температура в
том материале, который является лучшим
теплоизолятором или имеет меньшее
значение λ.
Распределение
температур в пределах каждого слоя –
линейное, однако в различных слоях угол
наклона температурной прямой отличается:
более резко изменяется температура в
том материале, который является лучшим
теплоизолятором или имеет меньшее
значение λ.
