.2.Закон Фурье

Согласно гипотезе Фурье, количество теплоты d²Q_τ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту  :

.

(9.4)

Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:

.

(9.5)

Проекции вектора q на координатные оси соответствено

;    ;    .

Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.

Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком:

.

(9.6)

Полное количество теплоты, прошедшее через эту поверхность за время τ, определится из уравнения

.

(9.7)

9.3.Коэффициент теплопроводности

Коэффициент теплопроводности является физическим параметром вещества, характеризующим его способность проводить теплоту. Коэффициент теплопроводности определяется из уравнения (9.4):

.

(9.8)

Численно коэффициент теплопроводности равен количеству теплоты, проходящему в единицу времени через единицу изотермической поверхности при условии gradt=1. Его размерность Вт/(м·К). Значения коэффициента теплопроводности для различных веществ определяются из справочных таблиц, построенных на основании экспериментальных данных. Для большинства материалов зависимость коэффициента теплопроводности от температуры приближенно можно выразить в виде линейной функции

.

(9.9)

где λ₀ — значение коэффициента теплопроводности при температуре t₀=0 ⁰С; b — постоянная, определяемая опытным путем.

Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и составляет 0,006÷0,6 Вт/(м·К). Следует отметить, что верхнее значение относится к гелию и водороду, коэффициент теплопроводности которых в 5—10 раз больше, чем у других газов. Коэффициент теплопроводности воздуха при 0 ⁰С равен 0,0244 Вт/(м·К).

Для жидкости λ=0,07÷0,7 Вт/(м·К) и, как правило, уменьшается с увеличением температуры. Коэффициент теплопроводности воды с увеличением температуры возрастает до максимального значения 0,7 Вт/(м·К) при t=120 ⁰С и дальше уменьшается.

Наилучшими проводниками теплоты являются металлы, у которых λ=20÷418 Вт/(м·К). Самый теплопроводный металл — серебро. Для большинства металлов коэффициент теплопроводности убывает с возрастанием температуры, а также при наличии разного рода примесей. Поэтому коэффициент теплопроводности легированных сталей значительно ниже, чем чистого железа.

Материалы с λ<0,25 Вт/(м·К), обычно применяемые для тепловой изоляции, называют теплоизоляционными. Большинство теплоизоляционных и строительных неметаллических материалов имеют пористое строение, что не позволяет рассматривать их как сплошную среду.
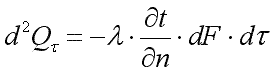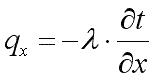
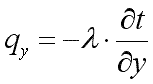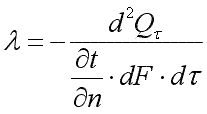