29. Навести схему та приклад перевірки гіпотези про вид закону розподілу генеральної сукупності за даними вибірки.

Задано емпіричний розподіл неперервної випадкової величини Х у вигляді послідовності інтервалів х і-1 – хі та відповідним їм частот пі , причому сума пі = п (обєму вибірки). Треба, використовуючи критерій Пірсона, перевірити гіпотезу про те, що випадкова величина Х розподілена рівномірно.

П равило. Для того, щоб перевірити гіпотезу про рівномірний розподіл Х , тобто за законом: 1/(в-а) в інтервалі (а, в)

f(x) = 0 поза цим інтервалом.

Треба:

1. Оцінити параметри а та в – кінці інтервалу, в якому спостереджувались можливі значення Х, за формулами:

А*=

2. знайти щільність імовірності предполагаемого розподілу f(x)= 1/(в* - а*)

3. Знайти теоретичні частоти:

4. Порівняти емпіричні та теоретичні частоти за допомогою критерія Пірсона, прийняв число степеней вільності к=s-3, де s – число інтервалів на яке розбита вибірка.

Приклад: чому параметри а і в рівномірно розподілені випадковою величиною Х оцінюються за формулою: а*=

Розвязок: Відомо, що в якості оцінок математичного сподівання і середнього квадратичного відхилення випадкової величини Х можно прийняти відповідно виборочну середню ֿхв та виборочне середнє квадратичне відхилення.

Відомо також, що для рівномірного розподілу математичне сподівання та середнє квадратичне відхилення відповідно дорівнюють:

М(х)=(а+в)/2,

Тому для оцінки параметрів рівномірного розподілу отримаємо систему двох лінійних рівнянь:

Вирішивши цю систему, отримаємо а*=

30. Дати означення поняття імовірності випадкової події. Сформулювати класичне визначення імовірності події і записати відповідну формулу. Навести приклади. Назвати основні фактори, що обмежують застосування класичного визначення імовірності. Сформулювати геометричне визначення імовірності. Навести приклад. Дати означення частоти та відносної частоти події.

Ймовірність випадкової події є кількісна міра об’єктивної можливості появи цієї події.

Класичне визначення ймовірності.

Імовірність події А дорівнює відношенню числа елементарних наслідків, які сприяють появі події А, до загального числа усіх єдиноможливих та рівно можливих елементарних наслідків.

Де к – число елементарних наслідків, що сприяють події А,

п – число усіх єдино можливих та рівно можливих наслідків.

Якщо k=0, Р(А)=0 – ймовірність неможливої події.

Якщо k=п, Р(А)=1 – ймовірність достовірної події.

Приклад: Серед 30 деталей у ящику 10 нестандартних. Ймовірність того, що навмання вийнята з ящику деталь – нестандартна Р = 10/30 = 1/3.

Основні фактори, що обмежують застосування класичного визначення ймовірності.

1. рівноможливость всіх елементарних наслідків експерименту.

2. скінченность або зліченность простору елементарних наслідків.

3.можливость представлення подій, ймовірність яких треба обчислити, як суму елементарних наслідків.

Геометричне визначення ймовірності.

Імовірність випадкової події А дорівнює відношенню міри g до міри G

(може використовуватись у випадку, коли всі елементарні наслідки рівноможливі, але простір елементарних наслідків є незлічена множина, яка займає деяку область G).

Нехай появі події А сприяє деяка її частина g, gG.

Приклад. Є квадрат зі стороною а, у який вписане коло. В цей квадрат навмання кидають кулю. Знайти ймовірність того, що куля впаде за колом.

Розв’язок.

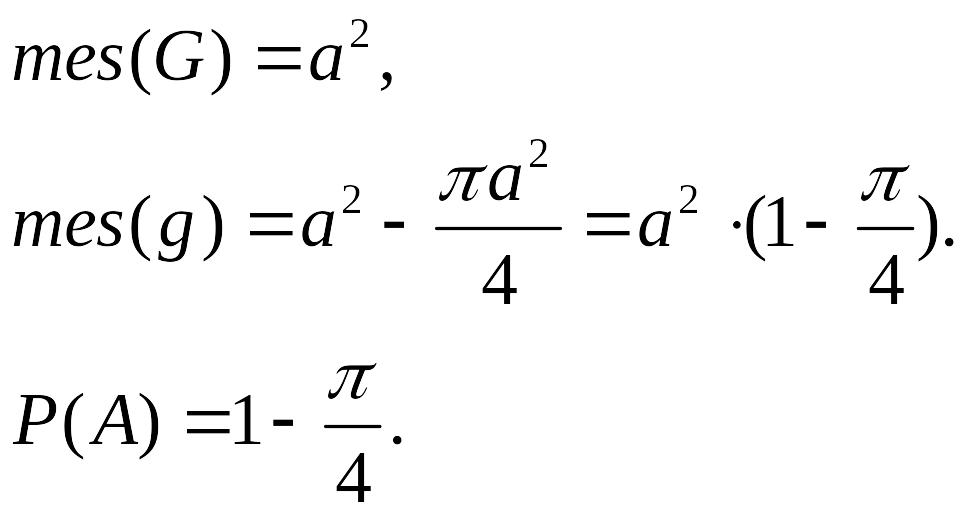
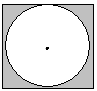
Нехай деякий експеримент, в результаті якого деяка подія А може з’явитися 1 раз (або не з’явитись) проводиться п раз і в m експериментах з’явилася 1 раз. Число m наз. частотою появи події А в п експериментах.

Число W(A)=m/n називають відносною частотою появи події А. Тобто це відношення числа випробувань, у яких подія А з’явилась, до числа фактично виконаних випробувань. Оскільки випадкова подія має властивість статистичної стійкості, то W(A) із змінною числа п буде мало змінюватись, коливаючись біля деякого числа, яке і буде ймовірністю появи події А.