24.Дати означення рівня значущості та потужності статистичного критерію. Пояснити способи знаходження одностороньої та двустороньої областей, імовірностний зміст рівня значущості.

Статистичним критерієм називають випадкову величину К, яка застосовується для перевірки гіпотези. Напиклад, якщо поревіряють гіпотезу про рівність дисперсій двох гернеральних сукупностей, то в якості критерію приймають відношення:

Спостережуваним значенням К_спост називають те значення критерію, яке обчислене по вибіркам. Наприклад, S²_i=20, S²_i=5,то F=20/5. Критичною областю називають такі значення критерія, при яких відкидають нульову гіпотезу. Областю прийняття гіпотези називають сукупність значення критерія, при якій нульову гіпотезу приймають. Критичними точками k_кр називають точки, що відділяють критичну область від області прийняття гіпотези. Правосторонньою (Лівосторонньою) критичною областю називають область , що визначається нерівністю K> (<) k_kr, де к_кр – додатнє (від‘ємне) число. Двосторонньою називають область, яка визначається нерівностями: К>k1, K<k2; при цьому k2>k1.

Досить малу ймовірність, при якій (у даній певній задачі) подія можна вважати практично неможливим, називають рівнем значимості. На практиці звичайно приймають рівні значимості, укладені між 0,01 і 0,05.

Потужністю критерію називають вірогідність попадання критерію в критичну область за умови, що справедлива конкуруюча гіпотеза. Іншими словами, потужність критерію є вірогідність того, що нульова гіпотеза буде знехтувана, якщо вірна конкуруюча гіпотеза.

Однобічної називають правобічну або лівосторонню критичну область.

Двосторонньої називають критичну область, обумовлену нерівностями K<k₁ K>k₂, де k₂> k₁

Зокрема, якщо критичні крапки симетричні

відносно нуля двостороння критична область визначається нерівностями (у припущенні; що k_kp>0): або рівносильною нерівністю

25. Дати означення сполучення та розміщення із n елементів по k, переставлення із n елементів. Записати позначення та формули для обчислення числа цих сполук. Навести приклади.

Розміщенням із n елементів по k називається упорядкована k-елементна підмножина n-елементної множини.

Переставленням із n елементів називається розміщення із m елементів по n.

Сполученням із n елементів по k називається будь-яка неупорядкована k-елементна підмножина n-елементної множини.

Приклад 1-1. Скількома способами можна розсадити 4 учнів на 25 місцях?

Шукане число дорівнює числу розміщень з 25 по 4:

Приклад 1-2. Скількома способами можна розташувати на полиці 4 книги (позначимо їх А, В, С, D)?

Шукане число способів дорівнює числу способів упорядкування множини, що складається з 4 елементів, тобто .

Приклад 1-3. Кості доміно можна розглядати як комбінації з повтореннями по два з семи цифр 0, 1, 2, 3, 4, 5, 6. Число всіх таких комбінацій дорівнює

26. Дати означення випадкового експерименту, випадкової події, неможливої та достовірної подій. Навести приклади. Дати означення елементарного наслідку випадкового експерименту, простору елементарних наслідків.

Експеримент (випробування) – реалізація певної сукупності умов, в результаті якої настає певна подія.

Експеримент наз. випадковим, якщо в результаті його проведення може настати деяка подія.

Випадковою називають таку подію, яка при умовах, що розглядаються,може трапитися, а може й не трапитися.

Неможливою називають таку подію, яка при розглянутих умовах не може трапитися.

Достовірною називають таку подію, яка при розглянутих умовах обов’язково трапиться.

Приклади: Якщо в урні є лише білі кулі, то добування білої кулі з урни – достовірна подія, а добування з цієї урни кулі іншого кольору – неможлива подія.

Якщо кинути монету на площину, то поява герба буде випадковою подією, тому що замість герба може з’явитися надпис.

Елементарний наслідок випадкового експерименту – така подія, яка не може бути сумою інших наслідків цього ж експерименту.

Множину всіх елементарних наслідків називають простором елементарних наслідків та експериментів.

Простір елементарних наслідків може містити скінчену (злічену) або незлічену множину елементів.

Приклад 1-1.

А ={1} – елементарний наслідок

B = { 4}

C = {1; 3}

D = {3}

C = AD – неелементарний наслідок.

Приклад 1-2.

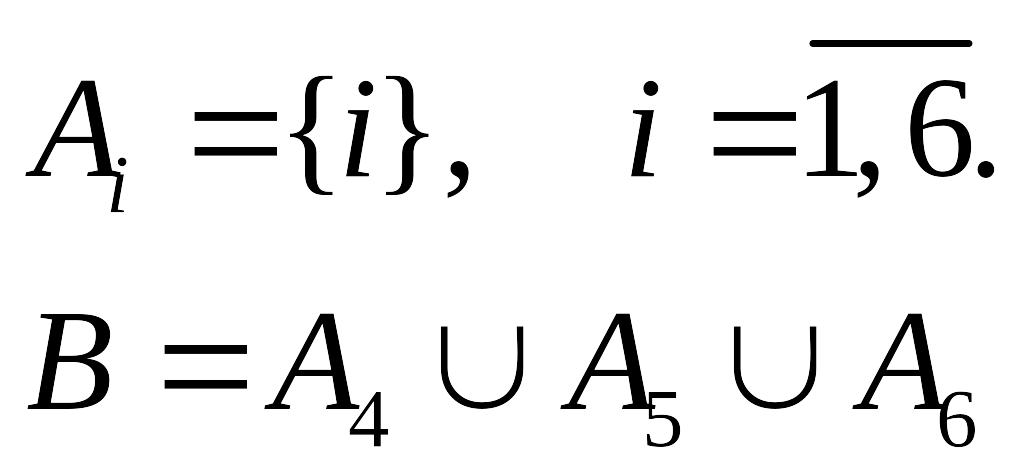- злічена множина елементів.