21.Що є предметом теорії ймовірностей? Дати визначення підмножини, скінченної, нескінченної, зліченої і незліченої множин. Навести приклади.

Предметом ТЙ є вивчення ймовірнісних закономірностей масових однорідних випадкових подій.

Підмножина – частина множини. Будь – яка множина є підмножиною самої себе. Множина наз. нескінченною (скінченною), якщо вона має нескінченне (скінченне) число елементів.

Нескінченна множина наз. зліченою (незліченою), якщо її елементи можна (неможна) пронумерувати.

Приклади:

1. якщо Х- множина відмінників групи, то 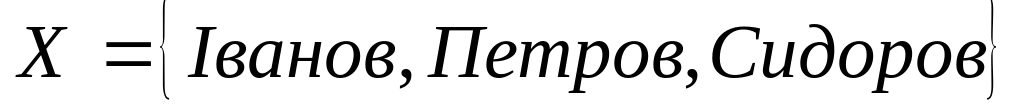- це спосіб завдання множини перерахуванням скінченної множини

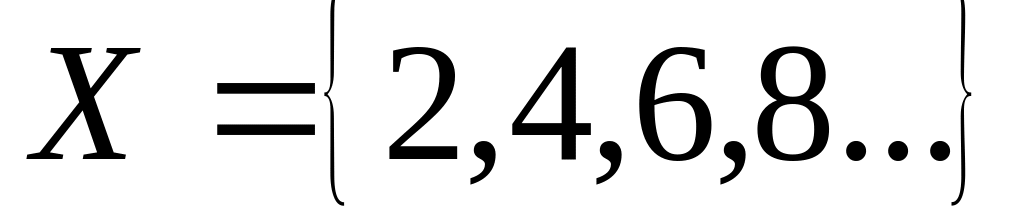2. - це спосіб завдання перерахуванням нескінченної множини;

22.Дати означення варіанти, варіаційного ряду,частоти,відносної частоти,статистичного розподілу вибірки. Навести приклади.

Нехай з генеральної сукупності зроблена деяка вибірка, при чому х1 спостерігалося n раз, х2-n2 раз, xk-nk разів і Σni=n-об‘єм вибірки. Значення хі називають варіантами, а послідовність варіант, записаних у зростаючомку порядку-варіаційним рядом. Числа спостережень називають частотами, а їх відношення до об‘єму вибірки – ni/n=Wi-відносними частотами. Статистичним розподілом вибірки називають перелік варіантів відповідних ним частот або відносних частот. Статистичних розподіл також можна задавати у вигляді послідовності інтервалів і відповідних їм частот.

Xi	2	6	12
Ni	3	10	7

W1=3/20=0.15; W2=10/20=0.5; W3=7/20=0.35

Xi	2	6	12
Wi	0.15	0.5	0.35

23.Дати означення функціональної, статистичної та кореляційної залежностей, умовного середнього, вибіркових рівняння та лінії регресії. Навести приклади.

Строга функціональна залежність реалізується рідко, так як обидві величини або одна з них підлягають ще дії випадкових факторів, при чому серед них можуть бути і загальні для обох величини. В цьому випадку виникає статистична залежність.

Наприклад, якщо Y залежить від випадкових факторів Z1,Z2,V1,V2, а X залежить від випадкових факторів Z1,Z2,U1, то між У та Х є статистична залежність, так як серед випадкових є спільні, а саме Z1,Z2.

Статистичною є залежність, при якій зміни одної з величин тягне за собою зміни розподілу іншої. Наприклад, статистична залежність проявляється в тому, що при зміні одної з величин змінюється середнє значення іншої, в цьому випадку статистичну залежність називають кореляційною.

Приклад. Нехай У-урожай зерна, Х-к-сть добрив. З однакових по площі землі при певних внесених добрив знімають різний урожай, тобто У не є функцією від Х. Але середній урожай залежить функціонально від кількості добрив, тобто У зв‘язаний з Х кореляційною залежністю.

Умовним середнім називають середнє арифметичне спостережуваних значень У, що відповідають Х=х, наприклад якщо при х1=2 величина у1=5, у2=6, у3=10, то умовне середнє =(5+6+10)/3=7.

Умовним середнім називають середнє арифметичне спостережуваних значень Х, що відповідають У=у.

Вибіркове рівняння регресії У на Х називають функцію вибіркової регресії У на Х, а її графік- вибірковою лінією регресії У на Х. Аналогічне рівняння