16. Запис. Осн. З-ни розподілу д.В.В.: а)біноміальн.; б)Пуассона; в)геометричн.

а) Биномиальным наз. распределение вер-стей, определяемое ф-лой Бернулли. Ф-ла Бернулли: , где k=0,1,2,…,n.

б) - эта ф-ла выражает з-н распред. Пуассона вер-стей массовых (n – велико) и редких (р – мало) событий.

в)Геом. з. Ймовірн. появи – р, ймов. непояви – q=1-p. Випробув. закінч-ся, як тільки з’явиться подія А. Х – це число випробувань до появи події А.

17. Навести схему та приклад перевірки гіпотези про значущість вибіркового коефіцієнта кореляції.

Выборочный коэфиц. корреляции определяется равенством: 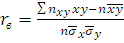, где x,y – варианты признаков значения X и Y; - частота пары вариант ( ); - объем выборки; - выборочные средние квадратические отклонения; - выборочные средние.

Если гипотеза о равенстве нулю генерального коэф. корреляции будет отвергнута, то значим, а величины X и Y коррелированны; если гипотеза принята, то незначим, а X и Y не коррелированны.

Правило для нормального распределения. Для того, чтобы при задано уровне значимости α проверить нулевую гипотезу : о равенстве нулю генерального коэф. корреляции нормальной двумерной случайной величины при конкурируещей гипотезе : , надо вычислить наблюдаемое значение критерия: и по таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы найти критическую точку для двусторонней критической области.

Если - нет оснований отвергнуть нулевую гипотезу.

Если - нулевую гипотезу отвергают.

Пример. По выборке объема n=122, извлеченной из нормальной двумерной совокупности, найдей выборочный коэф. корреляции . При уровне значимости 0,05 проверить нулевую гипотезу о равенстве нулю генерального коэф. корреляции при конкурирующей гипотезе : .

решение

так как по условию , то критическая область двусторонняя.

по уровню значимости 0,05 и k=122-2=120 находим по таблице приложения 6 для двусторонней критическ области критическую точку =1,98.

так как - нулевую гипотезу отвергаем. тоесть выборочн коэф корреляции значимо отличается от нуля.

18. Запис. Осн. З-ни розподілу н.В.В.: а)рівномірн; б)нормальн; в)показников.

а) розподіл ймовірностей наз. рівномірним, якщо на інтервалі, якому належать всі можливі значення випадкової величини, диференціальна ф-ція має стале значення. Диференц ф-ція рівномірн розподілу має вигляд:

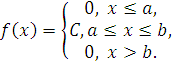де C=const.

б)показниковий розподіл – це розподіл, який описується ф-цією:

де , стала додатна величина

в) нормальним наз розподіл ймовірностей н.в.в. х, який описується на всій числовій осі диференціальною ф-цією (щільністю) , де а і - параметри нормального розподілу.

19.

20. Дати означ. Генеральн. Та вибірков. Середніх. Довести незміщенність вибірков. Середньої як оцінки генеральн. Середн. Сформулюв. Вл-ть стійкості вибіркових середніх.

Генеральной середней x_г наз. среднее арифметическое значений признака генеральной совокупности.

Если все значения х₁,х₂,…,х_N признаки генеральной совокупности объема N различны, то

х_г=(х₁+х₂+…+х_N)/N

Если значения признака х₁,х₂,…,х_N имеют соответственно частоты N₁,N₂,...,N_k, причем N₁+N₂+...+N_k=N, то

х_г=(x₁N₁+x₂N₂+...+x_kN_k)/N

Выборочной средней х_в наз. среднее арифметическое значение признака выборочной совокупности.

Если все значения х₁,х₂,…,х_n признаки выборки объема n различны, то

х_в=(х₁+х₂+…+х_n)/n

Если значения признака х₁,х₂,…,х_n имеют соответственно частоты n₁,n₂,...,n_k, причем n₁+n₂+...+n_k=n, то

х_в=(x₁n₁+x₂n₂+...+x_kn_k)/n

При увеличении объема выборки n выборочная средняя стремится по вероятности к генеральонй средней, а это означает, что выборочная средняя есть состоятельная оценка генеральной средней. Из сказаного следует, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом и состоит св-во устойчивости выборочных средних.