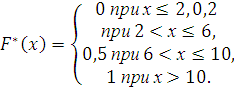- •1.Що в теорії ймовірностей розуміють під терміном «Закон великих чисел»? Записати нерівність а. Чебишова. Пояснити зміст букв.
- •2. Дати означення системи випадкових величин.
- •4. Для перевірки правильності основної статистичної гіпотези Но необхідно:
- •11. Дати означення емпіричної та теоретичної частот, записати формулу обчислення теоретичних частот для нормально розподіленої генеральної сукупності.
- •13. Сформулювати основні теореми закону великих чисел: а) Бернуллі б)Чебишова. Центральну граничну теорему. Пояснити зміст позначень.
- •14. Дати означення вибіркових: а)моди б) медіани в) початкового моменту г) центрального моменту д) асиметрії е) ексцесу
- •16. Запис. Осн. З-ни розподілу д.В.В.: а)біноміальн.; б)Пуассона; в)геометричн.
- •17. Навести схему та приклад перевірки гіпотези про значущість вибіркового коефіцієнта кореляції.
- •18. Запис. Осн. З-ни розподілу н.В.В.: а)рівномірн; б)нормальн; в)показников.
- •20. Дати означ. Генеральн. Та вибірков. Середніх. Довести незміщенність вибірков. Середньої як оцінки генеральн. Середн. Сформулюв. Вл-ть стійкості вибіркових середніх.
- •21.Що є предметом теорії ймовірностей? Дати визначення підмножини, скінченної, нескінченної, зліченої і незліченої множин. Навести приклади.
- •22.Дати означення варіанти, варіаційного ряду,частоти,відносної частоти,статистичного розподілу вибірки. Навести приклади.
- •24.Дати означення рівня значущості та потужності статистичного критерію. Пояснити способи знаходження одностороньої та двустороньої областей, імовірностний зміст рівня значущості.
- •25. Дати означення сполучення та розміщення із n елементів по k, переставлення із n елементів. Записати позначення та формули для обчислення числа цих сполук. Навести приклади.
- •27. Дати означення точкової та інтервальної оцінок параметра генеральної сукупності, точності, надійності (надійної імовірності), інтервальної оцінки, надійного інтервалу.
- •29. Навести схему та приклад перевірки гіпотези про вид закону розподілу генеральної сукупності за даними вибірки.
- •31.Дати означення статистичної оцінки параметру розподілу генеральної сукупності незміщеної, ефективної, обґрунтованої оцінок
- •32. Сформулювати теореми: а) про імовірність суми 2 подій; б) про імовірність суми 2 несумісних подій; в) про імовірність суми декількох попарно несумісних подій. Навести приклади
- •34. Вивести формули для обчислення параметрів вибіркового рівняння лінійної регресії. Пояснити зміст позначень. Навести приклади
- •35. Записати формули: а)повної імовірності; б) Байєса. Пояснити зміст позначень. Навести приклади.
- •37. Дати означення генеральної сукупності, вибіркової сукупності (вибірки), об’єму вибірки, повторної, безповторної та репрезентативної вибірок.
- •39. Дати визначення: а)полігону; б)гістограми; в)кумуляти частот та частостей. Назвати їх імовірнісний зміст. Навести приклади побудови.
- •40. Дати означення випадкової величини (в.В.), дискретної (д.В.В.) та неперервної (н.В.В.) випадкових величин.
- •41.Дати означення статистичної гіпотезти. Назвати основні види статистичних гіпотез. Дати означення нульової та альтернативної гіпотез. Дати означення помилки першого роду. Навести приклади.
- •44.Дати означення вибіркових: а)моди; б) медіани; в)початкового моменту; г)центрального моменту; д)асиметрії; е)ексцесу. Записати формули, для їх обчислення. Пояснити зміст позначень, навести
- •47. Вивести рівняння лінійної середньоквадратичної регресії y та X (y на X). Пояснити зміст позначень. Дати означення коефіцієнту регресії, залишкової дисперсії та пояснити, що вони характеризують.
- •48. Дати означення генеральної та вибіркової середніх. Довести незміщеність вибіркової середньої як оцінки генеральної середньої. Сформулювати властивість стійкості вибіркових середніх.
- •49. Записати випадкові величини, які мають розподіли: а) Пірсона; б)Стьюдента; в)Фішера. Записати функції щільності розподілу ймовірностей для цих розподілів. Пояснити зміст позначень.
- •51. Записати формули для обчислення математичного сподівання та дисперсії : а) функції д.В.В.; б) фцнкції н.В.В. Пояснити зміст позначень. Навести приклади.
- •52. Дати означення емпіричної та теоретичної частот, записати формулу для обчислення теоретичних частот для розподілу Пуассона.
11. Дати означення емпіричної та теоретичної частот, записати формулу обчислення теоретичних частот для нормально розподіленої генеральної сукупності.
А) Емпіричними частотами називають фактично спостерігаємі частоти ni. Нехай є наміри допустити, що вивчаєма величина Х розподілена по деякому визначеному законом. Щоб перевірити, чи співпадає дане припущення з даними спостереження., вичисляють частоти спостерігаємих значень, тобто знаходять теоретичну частоту ni кожного з спостерігаємих значень в припущення, що величина Х розподілена по припущеному закону. Теоретичні, на відміну від фактичних спостережуваних емпіричних частот називають частоти ni, знайдені теоретично (вичисленням). Теоретичні частоти знаходять за допомогою рівності ni=Рі* n.
Для розподілу Пуассона:
![]()
Б) У випадку, коли ВВ розподілена нормально, то вирівнюючі частоти можуть бути знайдені за формулою:
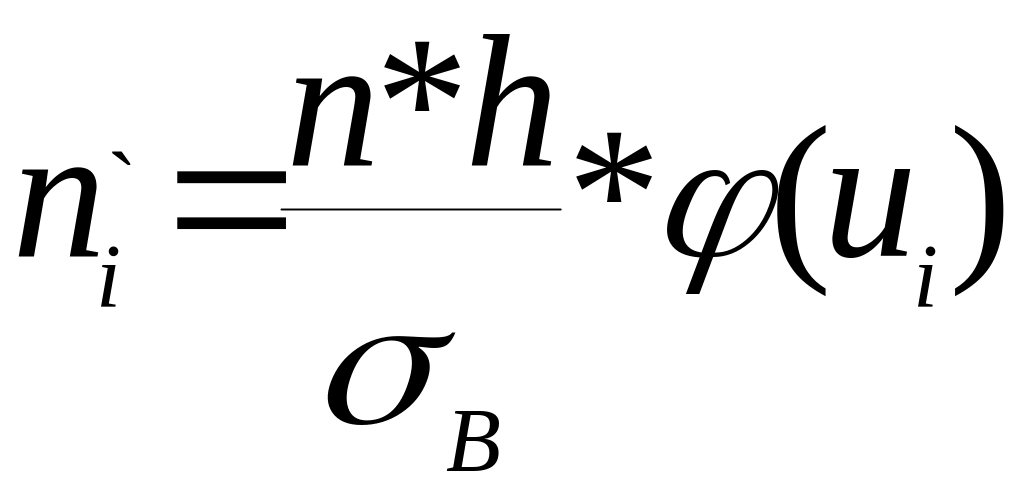
Де n- число випробувань
(об‘єм вибірки), h-довжина
часткового інтервалу, σ-вибіркове
середньоквадратичне відхилення,
ui=(xi-![]() B)/σ.
B)/σ.
Наприклад, для розподілу Пуассона:
xi |
15 |
20 |
25 |
30 |
ni |
6 |
13 |
38 |
74 |
Р(0)=0,33469, Р(1)=0,0,251021,….
Вир |
116 |
174 |
131 |
65 |
Хв=34,7. σв=7,38.
12. Записати формули для обчислення вибіркового коефіцієнта кореляції, кінців надійного інтервалу для інтервальної оцінки коефіцієнта кореляції нормально розподіленої генеральної сукупності. Пояснити зміст позначень.
Вибірковий коефіцієнт кореляції
визначається
![]() , де x,y
–варіанти ознак X та Y,
nxy –
частота пари варіант, n
–обєм вибірки , σx
,σy –вибіркові
середні квадратичні відхилення,
,
-
вибіркові середні. Відомо, що якщо
величини Y та X
не залежать, то коефіцієнт кореляції
r=0, якщо r=
-1, то Y та Х зв´язані
лінійною функцією начальною залежністю,
звідси слідує, що коефіцієнт кореляції
вимірює силу лінійного зв´язку між Y
та Х. Вибірковий коефіцієнт кореляції
r – являється оцінкою
коефіцієнта кореляції r
генеральної сукупності і тому слугує
для виміру лінійного зв´язку між
величинами кількісними ознаками Х та
Y. Якщо вибірка має достатньо
великий об´єм та добре представляє
генеральну сукупність, то заключення
про щільність лінійної залежності між
ознаками, яке отримано за даними вибірки,
в відомій степені може бути розповсюджено
і на генеральну сукупність. Приклад –
для оцінки коефіцієнта кореляції ry
нормально розподіленої генеральної
сукупності (при np=50)
можна скористатися формулою:
, де x,y
–варіанти ознак X та Y,
nxy –
частота пари варіант, n
–обєм вибірки , σx
,σy –вибіркові
середні квадратичні відхилення,
,
-
вибіркові середні. Відомо, що якщо
величини Y та X
не залежать, то коефіцієнт кореляції
r=0, якщо r=
-1, то Y та Х зв´язані
лінійною функцією начальною залежністю,
звідси слідує, що коефіцієнт кореляції
вимірює силу лінійного зв´язку між Y
та Х. Вибірковий коефіцієнт кореляції
r – являється оцінкою
коефіцієнта кореляції r
генеральної сукупності і тому слугує
для виміру лінійного зв´язку між
величинами кількісними ознаками Х та
Y. Якщо вибірка має достатньо
великий об´єм та добре представляє
генеральну сукупність, то заключення
про щільність лінійної залежності між
ознаками, яке отримано за даними вибірки,
в відомій степені може бути розповсюджено
і на генеральну сукупність. Приклад –
для оцінки коефіцієнта кореляції ry
нормально розподіленої генеральної
сукупності (при np=50)
можна скористатися формулою:
13. Сформулювати основні теореми закону великих чисел: а) Бернуллі б)Чебишова. Центральну граничну теорему. Пояснити зміст позначень.



14. Дати означення вибіркових: а)моди б) медіани в) початкового моменту г) центрального моменту д) асиметрії е) ексцесу
Мода – це варіанта, яка має найбільшу частоту. Наприклад,
1 |
4 |
7 |
9 |
5 |
1 |
20 |
6 |
Мода = 7.
Медіаною me називається варіанта, яка ділить варіаційний ряд на дві частини, рівному по числу варіанти. Якщо число варіант непарне, тобто n=2k+1, тоді me=xk+1, при парному n=2k me=(xk+xk+1)/2. Наприклад, для ряду 2,3,5,6,7 медіана =5, а для ряду 2,3,5,6,7,9 (5+6)/2=5,5.
Початковим моментом к ВВ Х називається М(х) величини хк
![]()
Центральним моментом порядку k ВВ Х називається М(х) величини (х - М(х))к.
![]()
Асиметрією називають відношення центрального моменту третього порядку до кубу середньоквадратичного відхилення.
Аs=![]()
Ексцесом називають характеристику, яка визначається рівністю
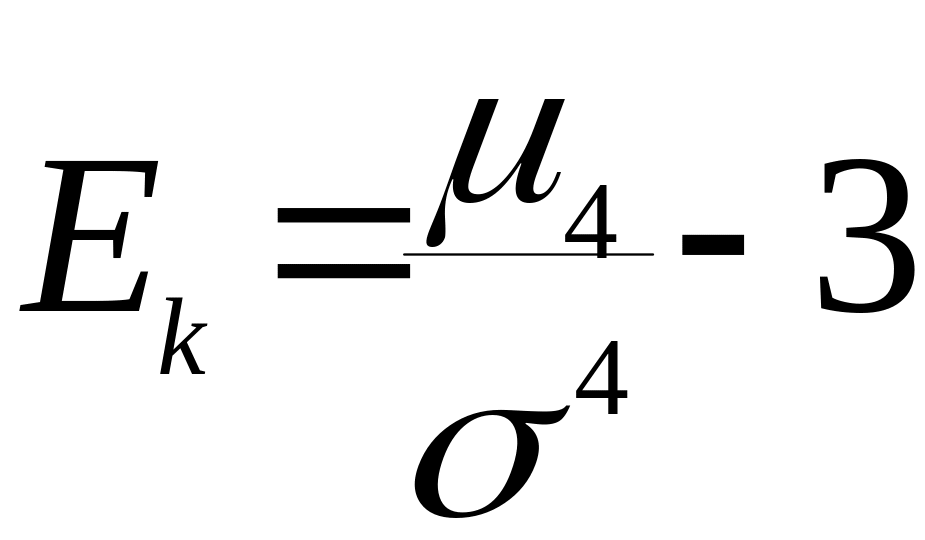
15. Дати означ. статистичн. (емпіричн.) ф-ції розподілу та навести її осн. вл-ті. Вказати різницю між емпіричн. та теоретичн. ф-ціями розпод. Навести прикл. побудови емпіричн. ф-ції розп. та її графіка.
Эмпирической ф-цией распред. (ф-цией
распред. выборки) наз. ф-цию ![]() ,
определяющую для каждого значения х
относительную частоту события Х<х.
,
определяющую для каждого значения х
относительную частоту события Х<х.
![]() ,
где
,
где ![]() - число вариант, меньших х;
- число вариант, меньших х; ![]() - объем выборки.
- объем выборки.
В отличие от эмпирической ф-ции распред.
выборки ф-цию распред. ![]() генеральной совокупности наз. теоретической
ф-цией распред. Различие межде эмперическ.
и теоретическ. ф-циями состоит в том,
что теоретическая ф-ция
определяет вероятность события Х<х,
а эмперическая ф-ция
определяет относительную частоту этого
же события.
генеральной совокупности наз. теоретической
ф-цией распред. Различие межде эмперическ.
и теоретическ. ф-циями состоит в том,
что теоретическая ф-ция
определяет вероятность события Х<х,
а эмперическая ф-ция
определяет относительную частоту этого
же события.
Свойства:
1)значения эмперическ ф-ции принадлеж
отрезку ![]()
2) - неубывающая ф-ция
3)если ![]() - наименьшая варианта, то
- наименьшая варианта, то ![]() при
при ![]() ;
если
;
если ![]() – наибольшая варианта,
– наибольшая варианта, ![]() при
при ![]() .
.
Значит, эмперическая ф-ция распред. выорки служит для оценки теоретической ф-ции распред. генеральной совокупности.
Пример. Построить эмперическ. ф-цию по данному распред. выборки:
Xi |
2 |
6 |
10 |
Ni |
12 |
18 |
30 |
Решение
объем выборки 12+18+30=60. наименьшая варианта = 2 → при х≤2.
Значения Х<6, а именно
=2,
наблюдалось 12 раз, → ![]() =0,2
при
=0,2
при ![]() .
.
Значения Х<10, а именно
=2
и ![]() =6,
наблюдалось 12+18=30 раз, →
=6,
наблюдалось 12+18=30 раз, → ![]() =0,5
при
=0,5
при ![]() .
.
так как х=10 –наибольшая варианта, то
при ![]() .
.