49. Записати випадкові величини, які мають розподіли: а) Пірсона; б)Стьюдента; в)Фішера. Записати функції щільності розподілу ймовірностей для цих розподілів. Пояснити зміст позначень.

А) Нехай Х_і(і=1, 2,…, n) – нормальні незалежні випадкові величини, причому математичне сподівання кожної із них рівне нулю, а середнє квадратичне відхилення – одиниці. Тоді сума квадратів цих величин

розподілена по закону с k=n степенями вільності; якщо ж ці величини зв’язані одним лінійним співвідношенням, наприклад , то число вільності k=n-1.

Щільність цього розподілу

, де

- гамма-функція, а саме Г(n+1)=n!

Звідси видно, що цей розподіл визначається одним параметром – числом степенів вільності k. Із збільшенням числа степенів вільності розподіл повільно наближається до нормального.

Б) Нехай Z – нормальна випадкова величина, причому М(Z)=0, , а V – незалежна від Z величина, яка розподілена по закону з k степенями вільності. Тоді величина

має розподіл, який називають t-розподілом або розподілом Стьюдента з k степенями вільності.

Отже, відношення нормованої нормальної величини до квадратного кореня із незалежної випадкової величини, розподіленої по закону з k степенями вільності, діленої на k, розподілено по закону Стьюдента з k степенями вільності.

Із збільшенням числа степенів вільності розподіл Стьюдента швидко наближається до нормального.

В) Якщо U і V – незалежні випадкові величини, розподілені по закону зі степенями вільності k₁ і k₂, то величина

має розподіл, який називають розподілом F Фішера-Снедекора зі степенями вільності k₁ і k₂ (інколи його позначають через V )

Щільність цього розподілу:

, де

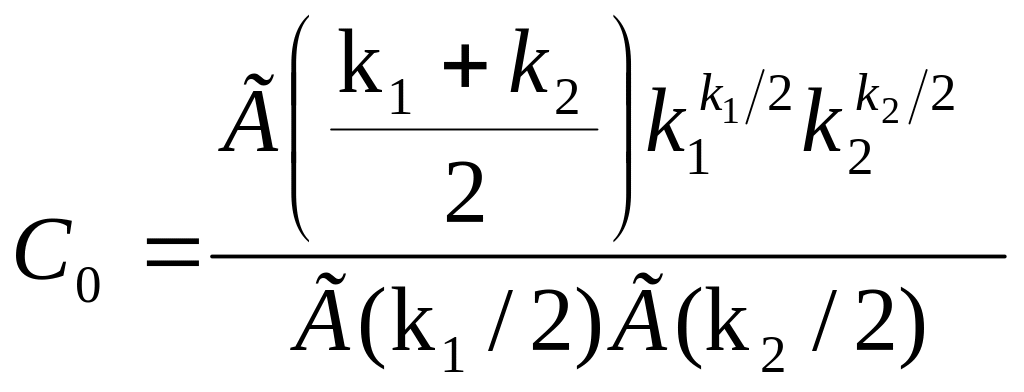
Розподіл F визначається двома параметрами – числами степенем вільності.

50. Дати означення функції випадкової величини. Записати формулу для знаходження щільностей імовірностей функції неперервного випадкового аргумента. Навести приклади побудови закону розподілу функції двв та щільності імовірностей функції нвв.

Функцією розподілу називають функцію F(x), що определяють ймовірність того, що випадкова величина Х в результаті випробування прийме значення, менше х, тобто F(x)=Р(Х<х).

Геометрично це рівність можна истолковать: F(x) це ймовірність того, що випадкова величина прийме значення, яке зображується на числовій осі точкою, що знаходиться лівіше від точки х.

Щільність розподілу ймовірностей НВВ Х називають функцію f(x) – першу похідну від функції розподілу F(x)

, з ціого означення випливає, що функція розподілу є першообразною для щільності розподілу

приклад

ДВВ Х задана таблицею розподілу Х 1 4 8\

Р 0,3 0,1 0,6

Знайти функцію розподілу та графік.

Розвязок якщо х<=1, то F(x)=0, Якщо 1<х<=4, то F(x)=0,3. Дійсно, х може прийняти значення 1 с ймовірністю 0,3

Якщо 4<х<=8, то F(x)=0,4. Дійсно, якщо х1 удовлєтворяє нерівності 4<х1<=8, то F(x)=ймовірності події Х<x1, яка може бути здійснене , коли Х прийме значення 1, або значення 4. Ці дві події не совмесні, то по теоремі складання імовірність події Х<х1, дорівнює сумі ймовірностей 0,3+0,1=0,4.

Якщо більше 8, то F(x)=1. Дійсно, подія х<=8 достовірна, тобто його ймовірність = 1.

Приклад2 Дана функція розподілу неперервної випадкової величини Х. знайти щільність.

Зв'язок: f(x)=