34. Вивести формули для обчислення параметрів вибіркового рівняння лінійної регресії. Пояснити зміст позначень. Навести приклади

Вибіркове рівняння регресії У на Х називають функцію вибіркової регресії У на Х, а її графік- вибірковою лінією регресії У на Х. Аналогічне рівняння

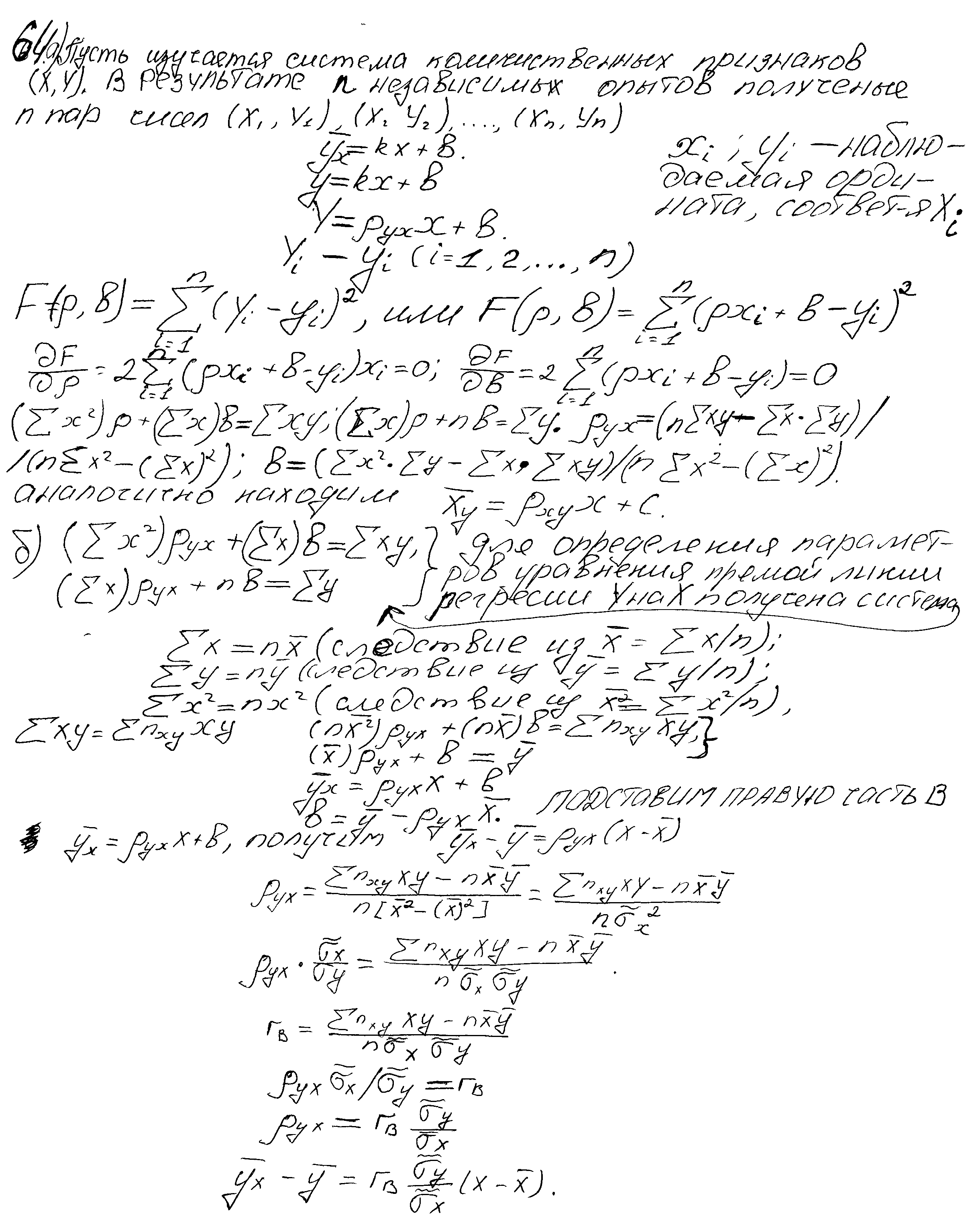
35. Записати формули: а)повної імовірності; б) Байєса. Пояснити зміст позначень. Навести приклади.

Формула повної ймовірності

, де - ймовірність появи події А, - ймовірність появи події , - ймовірність появи події А при умові, що перед тим з’явиться подія .

Формула Байєса:

,

де - ймовірність гіпотези після проведення експерименту, в результаті якого з’явилась подія А. - ймовірність гіпотези , - гіпотези А після проведення експерименту, в результаті якого з’явилась подія .

Приклад на Байєса: на фермах № 1 і № 2 відбулась спалах захворювання ящуром. Долі зараження 1/6 і 1/4. Випадково було відібрано із однієї ферми тварину, що захворіла. Знайти імовірність того, що ця тварина з першої ферми.

Р (В/А)=(1/2*1/6)/(1/2*1/6+1/2*1/4)=0,4

Відповідь: 0,4.

Приклад на повну імовірність: азотне добриво постачається з пунктів №1 і №2, при чому з першого пункта у 2р> ніж з другого.Імовірність події В1 (добриво з першого пункта задовольняє стандарт)=0,9, а відповідно імовірність для другого пункта=0,7. Знайти імовірність події А – взяте добриво відповідає стандарту.

Р(В1)=2/3, Р(В2)=1/3

Р(А)= Р(В1)*0,9+Р(В2)*0,7=2/3*0,9+1/3*0,7=0,83

36. Дати означення генеральних та вибіркових дисперсії та середнього квадратичного відхилення. Записати формули для їх обчислення, пояснити зміст позначень. Навести приклади. Пояснити необхідність використання виправленої дисперсії та записати формулу її обчислення.

Генеральною дисперсією D_Г називають середнє арифметичне квадратів відхилень значень ознаки генеральної сукупності від їх середнього значення .

Якщо всі значення х₁, х₂,…х_N ознаки генеральної сукупності об’єму N різні, то

.

Якщо значення ознаки х₁, х₂,…х_k мають відповідно частоти N₁, N₂,…N_k, причому N₁+ N₂+…+N_k=N, то

, тобто генеральна дисперсія є середньою зваженою квадратів відхилень із вагами, рівними відповідним частотам.

Наприклад Генеральна сукупність задана таблицею розподілу

х_і 2 4 5 6

N_i 8 9 10 3 Знайти генеральну дисперсію.

Розв’язання Знайдемо генеральну середню

Знайдемо генеральну дисперсію

Генеральним середнім квадратичним відхиленням називають корінь квадратний із генеральної дисперсії σ_Г=

Вибірковою дисперсією D_В називають середнє арифметичне квадратів відхилення спостерігаємих значень ознаки від їх середнього значення .

Якщо всі значення х₁, х₂,…х_N ознаки генеральної сукупності об’єму n різні, то

Якщо значення ознаки х₁, х₂,…х_k мають відповідно частоти n₁, n₂,…n_k, причому n₁+ n₂+…+n_k=n, то

. Отже, тобто вибіркова дисперсія є середньою зваженою квадратів відхилень із вагами, рівними відповідним частотам.

Наприклад Вибіркова сукупність задана таблицею розподілу

х_і 1 2 3 4

n_i 20 15 10 5 Знайти вибіркову дисперсію

Знайдемо вибіркову середню

Знайдемо вибіркову дисперсію

Вибірковим середнім квадратичним відхиленням (стандартом) називають квадратний корінь із вибіркової дисперсії: σ_В= .

Нехай із генеральної сукупності в результаті n незалежних спостережень над кількісною ознакою Х зроблена повторна вибірка об’єму n

Значення ознаки……………………… х₁ х₂ … х_k

Частоти ………………………………. n₁ n₂ … n_k

причому n₁+ n₂+…+n_k=n.

Необхідно за даними вибірки оцінити невідому генеральну дисперсію D_Г . якщо в якості оцінки генеральної дисперсії прийняти вибіркову дисперсію, то ця оцінка призводитиме до систематичних помилок, показуючи знижене значення генеральної дисперсії. Пояснюється це тим, що, як можна довести, вибіркова дисперсія є зміщеною оцінкою D_Г, іншими словами, математичне сподівання вибіркової дисперсії не рівно оцінюємої генеральної дисперсії, а рівне .

Легко «виправити» вибіркову дисперсію так, щоб її математичне сподівання було рівне генеральній дисперсії. Для цього достатньо помножити D_в на дріб .Зробивши це, ми отримаємо виправлену дисперсію, яку зазвичай позначають через S².