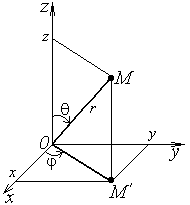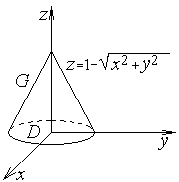1.2.2. Замена переменных в тройном интеграле.

Пусть в тройном интеграле прямоугольные координаты преобразуются к новым координатам которые связаны с соотношениями

(1.21)

которые однозначно разрешимы относительно :

. (1.22)

Обозначим через область в пространстве , в которую отображается область пространства с помощью формул (1.22).

Если функции (1.21) имеют в области непрерывные частные производные первого порядка и якобиан преобразования

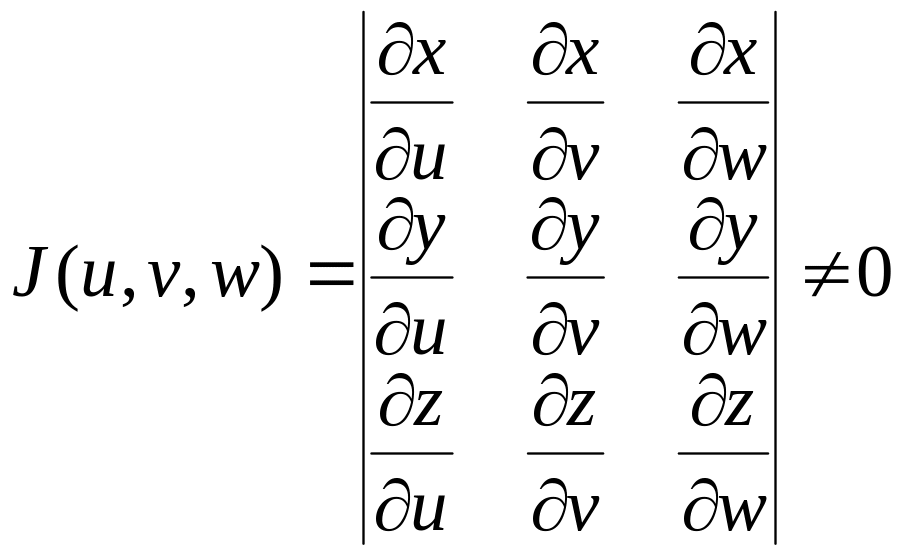
в области , то ограниченная замкнутая область пространства взаимно однозначно отображается на область пространства и для тройного интеграла имеет место следующая формула замены переменных:

(1.23)

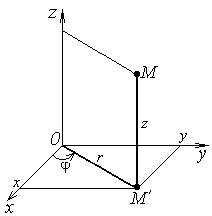
Цилиндрические координаты связаны с прямоугольными координатами соотношениями:

(1.24)

где (рисунок 1.10).

Рисунок 1.10

Рисунок 1.11

При переходе от прямоугольных координат к цилиндрическим координатам по формулам (1.24) поэтому формула (1.23) принимает вид

Если точка в пространстве имеет прямоугольные координаты , то сферическими координатами точки называют тройку чисел , где ― расстояние от точки до начала координат , ― угол между лучом ( ― проекция точки на плоскость ) и осью , ― угол между положительным направлением оси и лучом (рисунок 1.11).

Связь между прямоугольными и сферическими координатами определяется соотношениями где При этом и формула (1.23) принимает вид

Обобщенными сферическими координатами называют переменные , связанные с прямоугольными координатами формулами

где

Для обобщенных сферических координат и формула (1.23) имеет вид

3. . Примеры решения задач

Задача 1. Вычислить интеграл если область ограничена поверхностями и

Решение. Уравнение конической поверхности, ограничивающей область , можно записать в виде , а саму область представить следующим образом

где ― круг радиуса 1 с центром в начале координат (рисунок 1.12). Перейдем к цилиндрическим координатам где

Подынтегральная функция в цилиндрических координатах равна

Рисунок 1.12

якобиан перехода к цилиндрическим координатам равен Поэтому

Задача 2. Вычислить массу тела, ограниченного поверхностью и имеющего в каждой точке плотность

Решение. Поверхность, ограничивающая тело, является эллипсоидом, его каноническое уравнение полуоси

Согласно физическому смыслу тройного интеграла, масса тела, занимающего область , Перейдем к обобщенным сферическим координатам следовательно, уравнение эллипсоида имеет вид Поэтому для области координата изменяется от 0 до 1, угол ― от 0 до , а угол ― от 0 до Следовательно,

2. Криволинейные и поверхностные

ИНТЕГРАЛЫ ПЕРВОГО РОДА

1. . Криволинейные интегралы первого рода

Пусть на плоскости расположена ограниченная кривая , гладкая или кусочно-гладкая, функция определена и ограничена на кривой Разобьем кривую на частей не имеющих общих внутренних точек и на каждой из этих частичных дуг кривой возьмем произвольную точку и составим интегральную сумму

(2.1)

где ― длина -й частичной дуги

Пусть Если существует предел интегральной суммы (2.1) при не зависящей от способа дробления кривой на части и от выбора промежуточных точек то этот предел называется криволинейным интегралом 1-го рода от функции по кривой и обозначается

т.е. (2.2)

Из определения криволинейного интеграла следует, что его величина не зависит от того, в каком направлении обходят кривую

Кривая может быть замкнутой, в этом случае для обозначения криволинейного интеграла употребляют символ

Если ― длина кривой , то из формулы (2.2) при следует, что

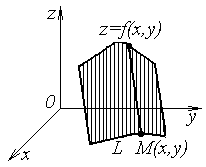
Если функция неотрицательна в точках кривой , то значение интеграла равно площади куска цилиндрической поверхности, которая образована перемещением перпендикуляра к плоскости по кривой и имеющего переменную длину (рисунок 2.1).

Если кривая - материальная, т.е. вдоль кривой распределена с плотностью некоторая масса то

Рисунок 2.1

С помощью криволинейных интегралов первого рода можно, как это делалось в случае двойных и тройных интегралов, находить моменты инерции материальной кривой относительно координатных осей, координаты центра масс кривой и т.д.

Если кривая задана параметрически: то

(2.3)

если кривая задана уравнением то

(2.4)

если кривая задана уравнением в полярных координатах то

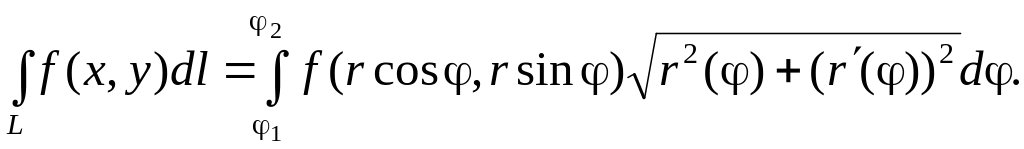(2.5)

Понятие криволинейного интеграла 1-го рода распространяется и на случай функции трех переменных заданной в точках пространственной кривой. Вычисление такого интеграла по кривой , заданной параметрически производится по формуле

. (2.6)